【核心素养目标】第四单元 《逻辑的力量》课件(共33张PPT)2023-2024学年统编版高中语文选择性必修上册
文档属性
| 名称 | 【核心素养目标】第四单元 《逻辑的力量》课件(共33张PPT)2023-2024学年统编版高中语文选择性必修上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 36.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 统编版 | ||
| 科目 | 语文 | ||
| 更新时间 | 2023-11-14 20:06:37 | ||
图片预览











文档简介
(共33张PPT)
逻辑的力量
第四单元
学习目标
1、建构初步的逻辑知识,提高语言运用能力,增强思维的敏锐性和严密性
2、通过辨析常见的逻辑错误,学会在具体的语境中判定逻辑谬误,准确使用语言
3、通过梳理三段论、假言推理等推理的有效形式,建立正确推理的观念,并能够辨别语言运用中的推理错误
4、学习论证,通过梳理探究论点、论据、论证形式等论证要素,学会分析议论性文章,在写议论性文章时,能够有效运用论证
导入:
④雷蒙德·斯穆里安是普林斯顿大学的博士生,一天他去纽约玩,遇到了一位非常迷人的女音乐家,斯穆里安对女音乐家说:“我们来做个游戏吧,我说一句话,如果这句话是真的,可以给我你的签名吗?”女音乐家饶有兴致地说:“当然,但如果你说的不是真的,我就不会给你。”
雷蒙德·斯穆里安说:
“好的……你既不会给我签名,也不会给我一个吻。”
就这样,斯穆里安巧妙地运用逻辑学赢得了一个香吻。
学习活动一:(6分钟)
1、阅读《高中语文阅读》(选必上)P119-121
回答(圈出课本原句):
①什么是概念?
②什么是概念的内涵和外延?
③概念和词语相同吗?是什么关系?哪些词语不能表示概念?
④概念之间有哪些关系?举出包含关系的例子。
⑤反对关系和矛盾关系有何区别?
阅读同时,圈出有疑惑的地方以便讲讨论。
概念的内涵和外延
概念的内涵和外延是相互依存、相互制约的。内涵是概念的质,它说明概念所反映的对象是什么样的;外延是概念的量,它说明概念所反映的是哪些对象。
判断正误:
商品是通过货币交换的劳动产品
思:小明的说法为何会引人发笑?
小明第一天上学回家后,表现得比较兴奋,妈妈很高兴,说明小明不排斥上学,而小明更是一个劲儿给妈妈讲发生在同学们之间的新鲜事。后来,妈妈问:“儿子,今天在课堂上老师都教了你什么?”小明偏着脑袋看着妈妈,表现出很不在乎的样子,说:“老师今天什么都没有教我,反而问我,‘一加二等于几’。”说到这里,小明停顿一下,用骄傲的口吻继续说:“老师真笨,这么简单的题都不会做,以后还怎么当我们的老师呀。”妈妈一听,笑着问道:“那你怎么回答她的呀?”小明说:“她不知道等于几,我只好教她,等于三呀。”
明确:
这则小故事中,儿子的回答很天真,他引人发笑的逻辑基础是不懂得“教”的概念。
“教”这个概念所反映的事物范围是指把知识或技能传授给人的所有行为、过程或方式。比如,教师问那位小孩“一加二是几”,这种提问的方式就是一种传授知识的方式,因此,它属于“教”这个概念所反映的事物范围。那位小孩天真地以为老师的这种提问的教学方式不属于“教”的范围。这说明他对“教”这个概念所反映的事物范围也是不明确的。
概念是语词的思想内容,语词是概念的物质承担者、表现形式。任何概念都必须借助语词来表达,脱离语词的赤裸裸的概念是不存在的。
1.概念是一种思维形式,而语词是一种语言形式
2.所有的概念都要借助语词来表达,但并非所有的语词都表达概念
3.同一个概念可以用不同的语词表达
例如“羽状复叶、花白色或蓝紫色,结浆果的多年生草本植物的块茎”这一特征的概念,可以用“土豆”、“洋芋”、“马铃薯”等语词表达。
概念和词语
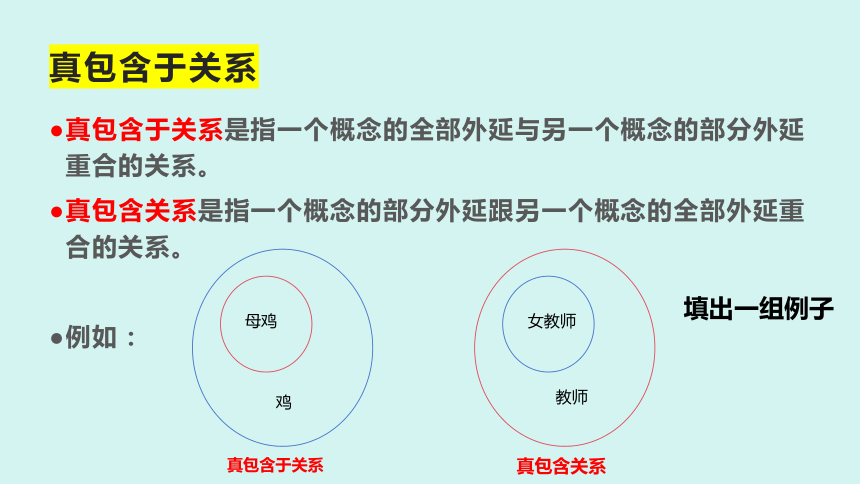
真包含于关系
真包含于关系是指一个概念的全部外延与另一个概念的部分外延重合的关系。
真包含关系是指一个概念的部分外延跟另一个概念的全部外延重合的关系。
例如:
真包含于关系
真包含关系
填出一组例子
母鸡
鸡
教师
女教师
定义
定义是揭示概念内涵的逻辑方法,给一个概念下定义就是用精炼的语句将这个概念的内涵揭示出来,也就是揭示这个概念所反映的对象的特有属性或本质属性。
定义是由被定义项、定义项和定义联项三部分构成的。在一个定义中,定义项是最重要的,我们给一个概念下定义,主要就是定义项。
例:“令尊”
补充:
定义的规则有以下四条:
1.定义必须是相应相称的
就是定义项的外延与被定义项的外延必须是全同关系,否则就会出现“ ”或“ ”的逻辑错误。
例如下面的例子:
思想是客观事物在人脑中的反映。
商品是通过货币进行交换的产品。
定义过宽
定义过窄
定义项的外延“客观事物在人脑中的反映”的外延大于被定义项“思想”的外延。这是因为感觉、直觉、表象也是客观事物在人脑中的反映,但它们不是思想——人类对客观事物的认识只有到了概念、判断、推理的思维阶段才能称得上是思想。
定义项“通过货币进行交换的产品”的外延小于定义项“商品”的外延。
定义过宽
定义过窄
2.定义项中不得直接或间接地包含被定义项
如果是直接包含被定义项,就会犯“同语反复”的错误。
如果是间接包含被定义项,就会犯“循环定义”的错误。
例:作家就是参加作家协会的人。
例:原因就是引起结果的事件,结果就是原因引起的事件。
儿子:爸爸,什么叫作“矛盾的论断”呢?
爸爸:矛盾的论断就是符合逻辑的论断。
儿子:那么,什么叫作“不合逻辑的论断”呢?
爸爸:唉,这还用得着再问吗,不符合逻辑的论断也就是矛盾的论断啊!
儿子:那到底什么是逻辑呀?
爸爸:嘿,我的小儿子,看来你真要打破砂锅问到底了。告诉你,逻辑呀,就是一门学问,这门学问嘛,就是专门讲逻辑的。
循环定义
问语反复
思:爸爸说清楚什么是逻辑了吗?
3.定义一般必须用肯定的语句形式和正概念
下定义是为了明确概念内涵的,也就是定义要明确指出一个概念具有哪些特有属性;而如果在下定义时用了否定句或者负概念,那么只能是写出了这个概念不具有哪些属性,但没有说明它具有哪些属性。
例如:
文学不是数学。×
文学是非数学。×
4.定义必须清楚确切
违反这条规则,就会犯“以比喻代定义”或者“定义语言含混”的错误。
例:
儿童是祖国的花朵。×
教师是人类灵魂的工程师。×
建筑是凝固的音乐。×
天文学就是研究天体结构和演变的科学。√
比喻是用跟甲事物有相似之点的乙事物来描写或说明甲事物,这里的甲事物就是本体,乙事物就是喻体,而本体和喻体是两个具有全异关系的概念,而不是下出定义时应该具有的属种关系的概念。
同一律
排中律
充足理由律
不矛盾律
学习活动二:阅读P117-P118
PPT模板 http:///moban/
充足理由律:在同一思维和论证过程中,一个思想被确定为真,要有充足的理由。要点:
①对所要论证的观点必须给出理由。
②给出的理由必须真实。
③给出的理由必须能够推出所要论证的论点。
常见的逻辑错误:
①“没有理由”②“理由虚假”③“推不出来”。如:
①送来的时候还好好的,怎么到你们医院之后就不行了呢?
②小李结婚后就离开了公司,一定是他新婚夫人让他辞去这份工作的。
③他出生时天昏地暗,飞沙走石,注定此生不凡。
排中律
排中律的内容是:在同一思维过程中两个相互矛盾的思想不能同时为假,必有一真。排中律的公式是:A或者非A。
注意:
第一,排中律并不否认客观事物本身有可能存在两种以上的情况或某种中间状态。比如,在前和后、好和坏之间客观存在着不前不后、不好不坏的中间状态,或某种过渡形态,排中律是承认的。
排中律只适用于非此即彼两种可能的事物情况,而对于存在三种或三种以上可能的事物情况,就不能用排中律去衡量。比如,下象棋的结局有“输、赢、和”三种可能,当一个棋手被问及下棋结局时,他回答“既没有赢,也没有输”,并不违反排中律。因为这不是同时否定两个具有矛盾关系的判断,而是同时否定两个具有反对关系的判断。
第二,排中律也并不排除人们在认识过程中,由于对事物情况尚未确认或为跳出对方的陷阱而采取的“二不择一”的态度。
第三,排中律不适用于“复杂问语”,不能对“复杂问语”提供的“是”、“非”选择做出简单的肯定或否定,而应当从根本上推翻它;复杂问语是一种隐含着与实际情况不符或对方根本不能接受的假定。对“复杂问语”的回答,无论是肯定还是否定,其结果都承认了这个错误的假定。
你戒了烟没有?
①岳云鹏根据《牡丹之歌》改编了一首《五环之歌》,其中有这样几句歌词:“我把车子开上五环……我就是要上五环,啊,五环,你比四环多一环……”
以下故事违背了哪种规律?
同一律
②罗素悖论:1919年英国数学家罗素讲了一个趣事:有一个理发师,他规定,自己只给那些不给自己刮胡子的人刮胡子。那么请问:这个理发师该不该给自己刮胡子?
矛盾律
③某地在该不该修水库问题上有两种意见,水利局长说:“认为该修的意见不现实,我不同意;认为不该修的意见脱离实际,我也不同意。”
讨论:
排中律
④鲍西娅有三只匣子:金匣子、银匣子和铅匣子,三只匣子上分别刻有三句话。在这三只匣子中,只有一只匣子里放着一张鲍西娅的肖像。
鲍西娅许诺:如果有哪一个求婚者能通过这三句话,猜中肖像放在哪只匣子里,她就嫁给他。
金匣子上刻:“肖像不在此匣中”
银匣子上刻:”肖像在金匣中。”
铅匣子上刻:”肖像不在此匣中。”
同时,这三句话中只有一句是真话。聪明而英俊的巴萨尼奥来求婚了!
肖像到底在哪个盒子中?
学习活动三:阅读《高中语文阅读》(选必上)P123-P130 课本P97-P99(6分钟)
回答(圈出课本原句):
1、判断的真假断定依据什么?
2、判断的结构必须包括哪几部分?
3、正确的判断需要符合什么标准?
4、只有什么句子能够表示判断
5、复合推理的形式有哪三种?
回答:
1、判断的真假断定依据什么?
2、判断的结构必须包括哪几部分?
3、正确的判断需要符合什么标准?
4、只有什么句子能够表示判断
5、复合推理的形式有哪三种?
陈述句
主项、谓项、联项
一个判断能否表示被断定和断定的关系
符合客观实际
归纳推理、演绎推理、类比推理
演绎推理——三段论
三段论实际上是以一个大前提(一般性的原则)以及一个小前提(附属于一般性的原则的特殊化陈述),由此引申出一个符合大前提的结论(特殊化陈述)的过程。
大前提:金属是导体
小前提:铁是金属
结论:所以铁会导电
所有阔叶植物都是落叶的,
所有葡萄树都是阔叶植物,
所以,所有葡萄树都是落叶的。
上述推理中的共同因素就是“阔叶植物”。进行三段论推理,关键就是要看这个共同因素能否把两个前提连接起来推出结论。
符合三段论定义的有效推理形式有24种。
所有爱斯基摩土著人都是穿黑衣服的;
所有的北婆罗洲土著人都是穿白衣服的;
没有既穿白衣服又穿黑衣服的人;
H是穿白衣服的人。
基于以上事实,下列哪个判断必为真?
A.H是北婆罗洲土著人。
B.H不是爱斯基摩土著人。
C.H不是北婆罗洲土著人。
D.H是爱斯基摩土著人。
E.H既不是爱斯基摩土著人,也不是北婆罗洲土著人。
B
类比推理:
形式结构概括如下:
A对象具有c、d属性
B对象也具有c属性
B对象也具有d属性
如果说归纳推理是从个别到一般的推理,那么类比推理则是从个别到另一个个别的推理。
邹忌的推理前提只是“闺房小语”,结论却是国家大事,结论和前提分别属于不同的范畴。可见,类比推理也是一种或然性推理,其推理的强度甚至比归纳推理更弱,但它在探究(人对物)和说理(人对人)活动中有着重要的作用。
柯南道尔的《银色马》中,主人公福尔摩斯有这样一段话:
马厩中有一条狗,然而,尽管有人进来,并且把马牵走,它竟毫不吠叫,没有惊动睡在草料棚里两个看马房的人。显然,这位午夜来客是这条狗非常熟悉的人。
这段话是一个论证,思考其表述出来的论据在逻辑上是否足够证明论点,如不能,说明存在隐含前提,试在方框内补写隐含前提。
1、关注论证的隐含前提
柯南道尔的《银色马》中,主人公福尔摩斯有这样一段话:
马厩中有一条狗,然而,尽管有人进来,并且把马牵走,它竟毫不吠叫,没有惊动睡在草料棚里两个看马房的人。显然,这位午夜来客是这条狗非常熟悉的人。
这段话是一个论证,思考其表述出来的论据在逻辑上是否足够证明论点,如不能,说明存在隐含前提,试在方框内补写隐含前提。
1、关注论证的隐含前提
狗吠叫会惊醒草料棚的人
不熟悉的人牵走马狗会吠叫
排除法
反证法,就是先假设与某个论点相矛盾的观点成立,然后推出明显的错误或矛盾,从而间接地证明最初的论点。多用于立论。
例:《拿来主义》
排除法,又叫“选言证法”或“淘汰法”,这是一种通过否定与论点相关的其他几种判断,从而确定论题为真的论证方法。
反证法
《拿来主义》
归谬法
归谬法则是从某一观点推出明显的错误或矛盾,从而证明这一观点本身的错误,常用于驳论。
例如:“逆境有利出人才”的命题,不但经不住事实检验,而且也经不住逻辑的推敲。试想,如果“逆境有利出人才”的命题能够成立,那么我们为了造就更多更好的人才,就应该为青少年去创造“逆境”了,如此推演下去,“改善办学条件”“创造良好的家庭环境”不都反而不利出人才了吗?真是荒谬之极!
推理经典题目:住中间房间的人是谁?
张涛、李明和赵亮三人住在三个相邻的房间内,他们之间满足这样的条件:
(1)每个人喜欢一种宠物,一种饮料,一种啤酒,不是兔就是猫,不是果粒橙就是葡萄汁,不是青岛就是哈尔滨;
(2)张涛住在喝哈尔滨者的隔壁;
(3)李明住在爱兔者的隔壁;
(4)赵亮住在喝果粒橙者的隔壁;
(5)没有一个喝青岛者喝果粒橙;
(6)至少有一个爱猫者喜欢喝青岛啤酒;
(7)任何两人的相同爱好不超过一种。
(8)至少有一个喝葡萄汁者住在一个爱兔者的隔壁;
小结:
驳论适用: 排除法 反证法 归谬法
思路: 驳→立
逻辑的力量
第四单元
学习目标
1、建构初步的逻辑知识,提高语言运用能力,增强思维的敏锐性和严密性
2、通过辨析常见的逻辑错误,学会在具体的语境中判定逻辑谬误,准确使用语言
3、通过梳理三段论、假言推理等推理的有效形式,建立正确推理的观念,并能够辨别语言运用中的推理错误
4、学习论证,通过梳理探究论点、论据、论证形式等论证要素,学会分析议论性文章,在写议论性文章时,能够有效运用论证
导入:
④雷蒙德·斯穆里安是普林斯顿大学的博士生,一天他去纽约玩,遇到了一位非常迷人的女音乐家,斯穆里安对女音乐家说:“我们来做个游戏吧,我说一句话,如果这句话是真的,可以给我你的签名吗?”女音乐家饶有兴致地说:“当然,但如果你说的不是真的,我就不会给你。”
雷蒙德·斯穆里安说:
“好的……你既不会给我签名,也不会给我一个吻。”
就这样,斯穆里安巧妙地运用逻辑学赢得了一个香吻。
学习活动一:(6分钟)
1、阅读《高中语文阅读》(选必上)P119-121
回答(圈出课本原句):
①什么是概念?
②什么是概念的内涵和外延?
③概念和词语相同吗?是什么关系?哪些词语不能表示概念?
④概念之间有哪些关系?举出包含关系的例子。
⑤反对关系和矛盾关系有何区别?
阅读同时,圈出有疑惑的地方以便讲讨论。
概念的内涵和外延
概念的内涵和外延是相互依存、相互制约的。内涵是概念的质,它说明概念所反映的对象是什么样的;外延是概念的量,它说明概念所反映的是哪些对象。
判断正误:
商品是通过货币交换的劳动产品
思:小明的说法为何会引人发笑?
小明第一天上学回家后,表现得比较兴奋,妈妈很高兴,说明小明不排斥上学,而小明更是一个劲儿给妈妈讲发生在同学们之间的新鲜事。后来,妈妈问:“儿子,今天在课堂上老师都教了你什么?”小明偏着脑袋看着妈妈,表现出很不在乎的样子,说:“老师今天什么都没有教我,反而问我,‘一加二等于几’。”说到这里,小明停顿一下,用骄傲的口吻继续说:“老师真笨,这么简单的题都不会做,以后还怎么当我们的老师呀。”妈妈一听,笑着问道:“那你怎么回答她的呀?”小明说:“她不知道等于几,我只好教她,等于三呀。”
明确:
这则小故事中,儿子的回答很天真,他引人发笑的逻辑基础是不懂得“教”的概念。
“教”这个概念所反映的事物范围是指把知识或技能传授给人的所有行为、过程或方式。比如,教师问那位小孩“一加二是几”,这种提问的方式就是一种传授知识的方式,因此,它属于“教”这个概念所反映的事物范围。那位小孩天真地以为老师的这种提问的教学方式不属于“教”的范围。这说明他对“教”这个概念所反映的事物范围也是不明确的。
概念是语词的思想内容,语词是概念的物质承担者、表现形式。任何概念都必须借助语词来表达,脱离语词的赤裸裸的概念是不存在的。
1.概念是一种思维形式,而语词是一种语言形式
2.所有的概念都要借助语词来表达,但并非所有的语词都表达概念
3.同一个概念可以用不同的语词表达
例如“羽状复叶、花白色或蓝紫色,结浆果的多年生草本植物的块茎”这一特征的概念,可以用“土豆”、“洋芋”、“马铃薯”等语词表达。
概念和词语
真包含于关系
真包含于关系是指一个概念的全部外延与另一个概念的部分外延重合的关系。
真包含关系是指一个概念的部分外延跟另一个概念的全部外延重合的关系。
例如:
真包含于关系
真包含关系
填出一组例子
母鸡
鸡
教师
女教师
定义
定义是揭示概念内涵的逻辑方法,给一个概念下定义就是用精炼的语句将这个概念的内涵揭示出来,也就是揭示这个概念所反映的对象的特有属性或本质属性。
定义是由被定义项、定义项和定义联项三部分构成的。在一个定义中,定义项是最重要的,我们给一个概念下定义,主要就是定义项。
例:“令尊”
补充:
定义的规则有以下四条:
1.定义必须是相应相称的
就是定义项的外延与被定义项的外延必须是全同关系,否则就会出现“ ”或“ ”的逻辑错误。
例如下面的例子:
思想是客观事物在人脑中的反映。
商品是通过货币进行交换的产品。
定义过宽
定义过窄
定义项的外延“客观事物在人脑中的反映”的外延大于被定义项“思想”的外延。这是因为感觉、直觉、表象也是客观事物在人脑中的反映,但它们不是思想——人类对客观事物的认识只有到了概念、判断、推理的思维阶段才能称得上是思想。
定义项“通过货币进行交换的产品”的外延小于定义项“商品”的外延。
定义过宽
定义过窄
2.定义项中不得直接或间接地包含被定义项
如果是直接包含被定义项,就会犯“同语反复”的错误。
如果是间接包含被定义项,就会犯“循环定义”的错误。
例:作家就是参加作家协会的人。
例:原因就是引起结果的事件,结果就是原因引起的事件。
儿子:爸爸,什么叫作“矛盾的论断”呢?
爸爸:矛盾的论断就是符合逻辑的论断。
儿子:那么,什么叫作“不合逻辑的论断”呢?
爸爸:唉,这还用得着再问吗,不符合逻辑的论断也就是矛盾的论断啊!
儿子:那到底什么是逻辑呀?
爸爸:嘿,我的小儿子,看来你真要打破砂锅问到底了。告诉你,逻辑呀,就是一门学问,这门学问嘛,就是专门讲逻辑的。
循环定义
问语反复
思:爸爸说清楚什么是逻辑了吗?
3.定义一般必须用肯定的语句形式和正概念
下定义是为了明确概念内涵的,也就是定义要明确指出一个概念具有哪些特有属性;而如果在下定义时用了否定句或者负概念,那么只能是写出了这个概念不具有哪些属性,但没有说明它具有哪些属性。
例如:
文学不是数学。×
文学是非数学。×
4.定义必须清楚确切
违反这条规则,就会犯“以比喻代定义”或者“定义语言含混”的错误。
例:
儿童是祖国的花朵。×
教师是人类灵魂的工程师。×
建筑是凝固的音乐。×
天文学就是研究天体结构和演变的科学。√
比喻是用跟甲事物有相似之点的乙事物来描写或说明甲事物,这里的甲事物就是本体,乙事物就是喻体,而本体和喻体是两个具有全异关系的概念,而不是下出定义时应该具有的属种关系的概念。
同一律
排中律
充足理由律
不矛盾律
学习活动二:阅读P117-P118
PPT模板 http:///moban/
充足理由律:在同一思维和论证过程中,一个思想被确定为真,要有充足的理由。要点:
①对所要论证的观点必须给出理由。
②给出的理由必须真实。
③给出的理由必须能够推出所要论证的论点。
常见的逻辑错误:
①“没有理由”②“理由虚假”③“推不出来”。如:
①送来的时候还好好的,怎么到你们医院之后就不行了呢?
②小李结婚后就离开了公司,一定是他新婚夫人让他辞去这份工作的。
③他出生时天昏地暗,飞沙走石,注定此生不凡。
排中律
排中律的内容是:在同一思维过程中两个相互矛盾的思想不能同时为假,必有一真。排中律的公式是:A或者非A。
注意:
第一,排中律并不否认客观事物本身有可能存在两种以上的情况或某种中间状态。比如,在前和后、好和坏之间客观存在着不前不后、不好不坏的中间状态,或某种过渡形态,排中律是承认的。
排中律只适用于非此即彼两种可能的事物情况,而对于存在三种或三种以上可能的事物情况,就不能用排中律去衡量。比如,下象棋的结局有“输、赢、和”三种可能,当一个棋手被问及下棋结局时,他回答“既没有赢,也没有输”,并不违反排中律。因为这不是同时否定两个具有矛盾关系的判断,而是同时否定两个具有反对关系的判断。
第二,排中律也并不排除人们在认识过程中,由于对事物情况尚未确认或为跳出对方的陷阱而采取的“二不择一”的态度。
第三,排中律不适用于“复杂问语”,不能对“复杂问语”提供的“是”、“非”选择做出简单的肯定或否定,而应当从根本上推翻它;复杂问语是一种隐含着与实际情况不符或对方根本不能接受的假定。对“复杂问语”的回答,无论是肯定还是否定,其结果都承认了这个错误的假定。
你戒了烟没有?
①岳云鹏根据《牡丹之歌》改编了一首《五环之歌》,其中有这样几句歌词:“我把车子开上五环……我就是要上五环,啊,五环,你比四环多一环……”
以下故事违背了哪种规律?
同一律
②罗素悖论:1919年英国数学家罗素讲了一个趣事:有一个理发师,他规定,自己只给那些不给自己刮胡子的人刮胡子。那么请问:这个理发师该不该给自己刮胡子?
矛盾律
③某地在该不该修水库问题上有两种意见,水利局长说:“认为该修的意见不现实,我不同意;认为不该修的意见脱离实际,我也不同意。”
讨论:
排中律
④鲍西娅有三只匣子:金匣子、银匣子和铅匣子,三只匣子上分别刻有三句话。在这三只匣子中,只有一只匣子里放着一张鲍西娅的肖像。
鲍西娅许诺:如果有哪一个求婚者能通过这三句话,猜中肖像放在哪只匣子里,她就嫁给他。
金匣子上刻:“肖像不在此匣中”
银匣子上刻:”肖像在金匣中。”
铅匣子上刻:”肖像不在此匣中。”
同时,这三句话中只有一句是真话。聪明而英俊的巴萨尼奥来求婚了!
肖像到底在哪个盒子中?
学习活动三:阅读《高中语文阅读》(选必上)P123-P130 课本P97-P99(6分钟)
回答(圈出课本原句):
1、判断的真假断定依据什么?
2、判断的结构必须包括哪几部分?
3、正确的判断需要符合什么标准?
4、只有什么句子能够表示判断
5、复合推理的形式有哪三种?
回答:
1、判断的真假断定依据什么?
2、判断的结构必须包括哪几部分?
3、正确的判断需要符合什么标准?
4、只有什么句子能够表示判断
5、复合推理的形式有哪三种?
陈述句
主项、谓项、联项
一个判断能否表示被断定和断定的关系
符合客观实际
归纳推理、演绎推理、类比推理
演绎推理——三段论
三段论实际上是以一个大前提(一般性的原则)以及一个小前提(附属于一般性的原则的特殊化陈述),由此引申出一个符合大前提的结论(特殊化陈述)的过程。
大前提:金属是导体
小前提:铁是金属
结论:所以铁会导电
所有阔叶植物都是落叶的,
所有葡萄树都是阔叶植物,
所以,所有葡萄树都是落叶的。
上述推理中的共同因素就是“阔叶植物”。进行三段论推理,关键就是要看这个共同因素能否把两个前提连接起来推出结论。
符合三段论定义的有效推理形式有24种。
所有爱斯基摩土著人都是穿黑衣服的;
所有的北婆罗洲土著人都是穿白衣服的;
没有既穿白衣服又穿黑衣服的人;
H是穿白衣服的人。
基于以上事实,下列哪个判断必为真?
A.H是北婆罗洲土著人。
B.H不是爱斯基摩土著人。
C.H不是北婆罗洲土著人。
D.H是爱斯基摩土著人。
E.H既不是爱斯基摩土著人,也不是北婆罗洲土著人。
B
类比推理:
形式结构概括如下:
A对象具有c、d属性
B对象也具有c属性
B对象也具有d属性
如果说归纳推理是从个别到一般的推理,那么类比推理则是从个别到另一个个别的推理。
邹忌的推理前提只是“闺房小语”,结论却是国家大事,结论和前提分别属于不同的范畴。可见,类比推理也是一种或然性推理,其推理的强度甚至比归纳推理更弱,但它在探究(人对物)和说理(人对人)活动中有着重要的作用。
柯南道尔的《银色马》中,主人公福尔摩斯有这样一段话:
马厩中有一条狗,然而,尽管有人进来,并且把马牵走,它竟毫不吠叫,没有惊动睡在草料棚里两个看马房的人。显然,这位午夜来客是这条狗非常熟悉的人。
这段话是一个论证,思考其表述出来的论据在逻辑上是否足够证明论点,如不能,说明存在隐含前提,试在方框内补写隐含前提。
1、关注论证的隐含前提
柯南道尔的《银色马》中,主人公福尔摩斯有这样一段话:
马厩中有一条狗,然而,尽管有人进来,并且把马牵走,它竟毫不吠叫,没有惊动睡在草料棚里两个看马房的人。显然,这位午夜来客是这条狗非常熟悉的人。
这段话是一个论证,思考其表述出来的论据在逻辑上是否足够证明论点,如不能,说明存在隐含前提,试在方框内补写隐含前提。
1、关注论证的隐含前提
狗吠叫会惊醒草料棚的人
不熟悉的人牵走马狗会吠叫
排除法
反证法,就是先假设与某个论点相矛盾的观点成立,然后推出明显的错误或矛盾,从而间接地证明最初的论点。多用于立论。
例:《拿来主义》
排除法,又叫“选言证法”或“淘汰法”,这是一种通过否定与论点相关的其他几种判断,从而确定论题为真的论证方法。
反证法
《拿来主义》
归谬法
归谬法则是从某一观点推出明显的错误或矛盾,从而证明这一观点本身的错误,常用于驳论。
例如:“逆境有利出人才”的命题,不但经不住事实检验,而且也经不住逻辑的推敲。试想,如果“逆境有利出人才”的命题能够成立,那么我们为了造就更多更好的人才,就应该为青少年去创造“逆境”了,如此推演下去,“改善办学条件”“创造良好的家庭环境”不都反而不利出人才了吗?真是荒谬之极!
推理经典题目:住中间房间的人是谁?
张涛、李明和赵亮三人住在三个相邻的房间内,他们之间满足这样的条件:
(1)每个人喜欢一种宠物,一种饮料,一种啤酒,不是兔就是猫,不是果粒橙就是葡萄汁,不是青岛就是哈尔滨;
(2)张涛住在喝哈尔滨者的隔壁;
(3)李明住在爱兔者的隔壁;
(4)赵亮住在喝果粒橙者的隔壁;
(5)没有一个喝青岛者喝果粒橙;
(6)至少有一个爱猫者喜欢喝青岛啤酒;
(7)任何两人的相同爱好不超过一种。
(8)至少有一个喝葡萄汁者住在一个爱兔者的隔壁;
小结:
驳论适用: 排除法 反证法 归谬法
思路: 驳→立
