2007年自主招生考试数学试卷及答案

浙江省慈溪中学2007年初中保送生招生考试数学试卷
（本卷考试时间90分钟，满分130分．）
一、选择题(每题6分，共30分)
1．将正方形ABCD折叠，使顶点A与CD边上的点M重合，
折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G(如图)．
如果DM：MC=3：2，则DE：DM：EM=( )
(A)7：24：25 (B)3：4：5 (C)5：12：13 (D)8：15：17
2．假期里王老师有一个紧急通知，要用电话尽快通知给50个同学,
假设每通知一个同学 需要1分钟时间，同学接到电话后也可以
相互通知，那么要使所有同学都接到通知最快需要的时间为( )
(A)8分钟 (B)7分钟 (C)6分钟． (D)5分钟
3．已知：二次函数y=+2x+a(a为大于0的常数)，当x=m时的函数值y<0；
则当x=m+2时的函数值y与0的大小关系为( )
(A)y2>0 (B)y2<0 (C)y2=O (D)不能确定
4．记S=
则S所在的范围为( )
(A)05．如图，点A是函数y=的图象上的点，点B、C
的坐标分别为B(-，-)、C(，)．
试利用性质：“函数y=的图象上任意一点A
都满足|AB-AC|=2”求解下面问题：
“作∠BAC的内角平分线AE，过B作AE的垂线交AE于F，
已知当点A在函数y=的图象上运动时，点F总在一条曲线上运动，则这条曲线为( )
(A)直线 (B)抛物线 (C)圆 (D)反比例函数的曲线
二、填空题(每题6分，共36分)
6．已知关于x的不等式(2a-b)x≥a-2b的解是x>，
则关于x的不等式ax+b<0的解为 ．
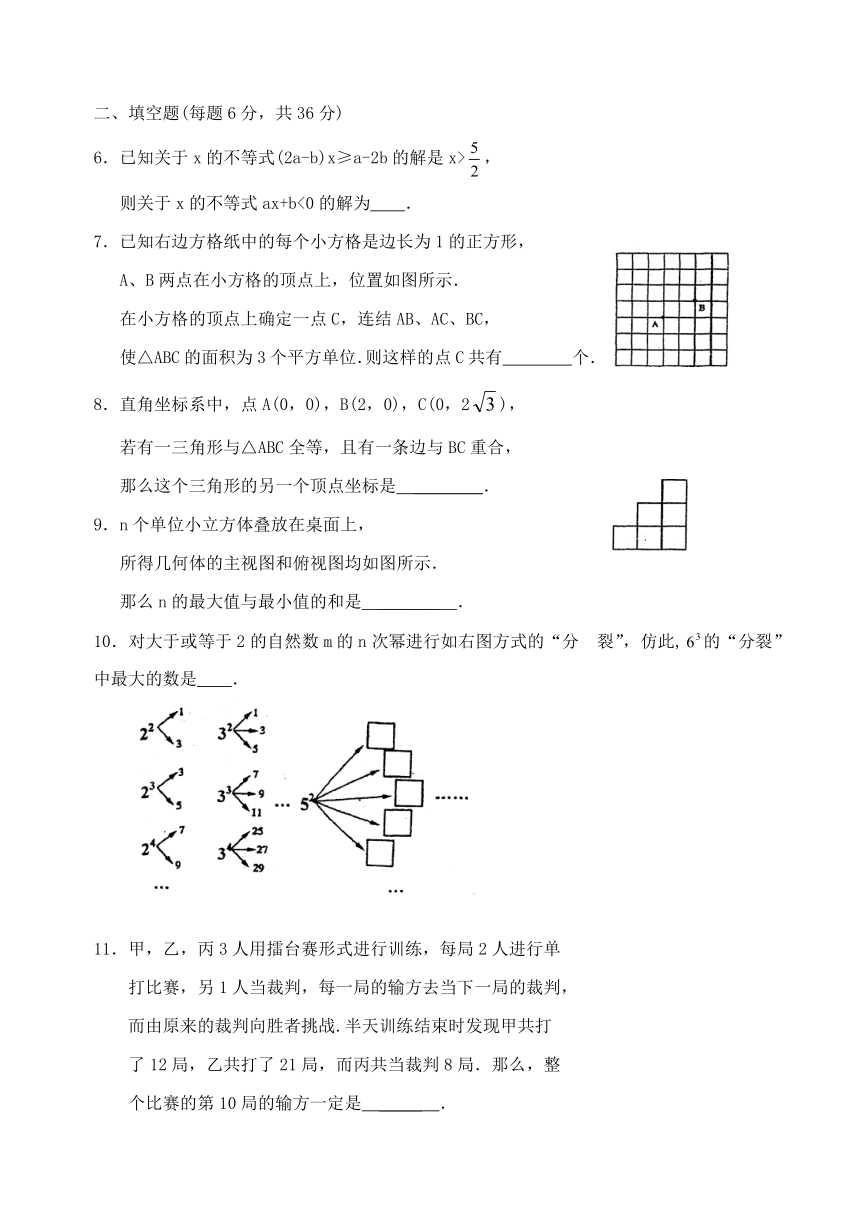
7．已知右边方格纸中的每个小方格是边长为1的正方形，
A、B两点在小方格的顶点上，位置如图所示．
在小方格的顶点上确定一点C，连结AB、AC、BC，
使△ABC的面积为3个平方单位．则这样的点C共有 个．
8．直角坐标系中，点A(0，0)，B(2，0)，C(0，2)，
若有一三角形与△ABC全等，且有一条边与BC重合，
那么这个三角形的另一个顶点坐标是 ________．
9．n个单位小立方体叠放在桌面上，
所得几何体的主视图和俯视图均如图所示．
那么n的最大值与最小值的和是 _______ ．
10．对大于或等于2的自然数m的n次幂进行如右图方式的“分 裂”，仿此,的“分裂”中最大的数是 ．
11．甲，乙，丙3人用擂台赛形式进行训练，每局2人进行单
打比赛，另1人当裁判，每一局的输方去当下一局的裁判，
而由原来的裁判向胜者挑战.半天训练结束时发现甲共打
了12局，乙共打了21局，而丙共当裁判8局．那么，整
个比赛的第10局的输方一定是 _____ ．
三、解答题(每小题16分，共64分)
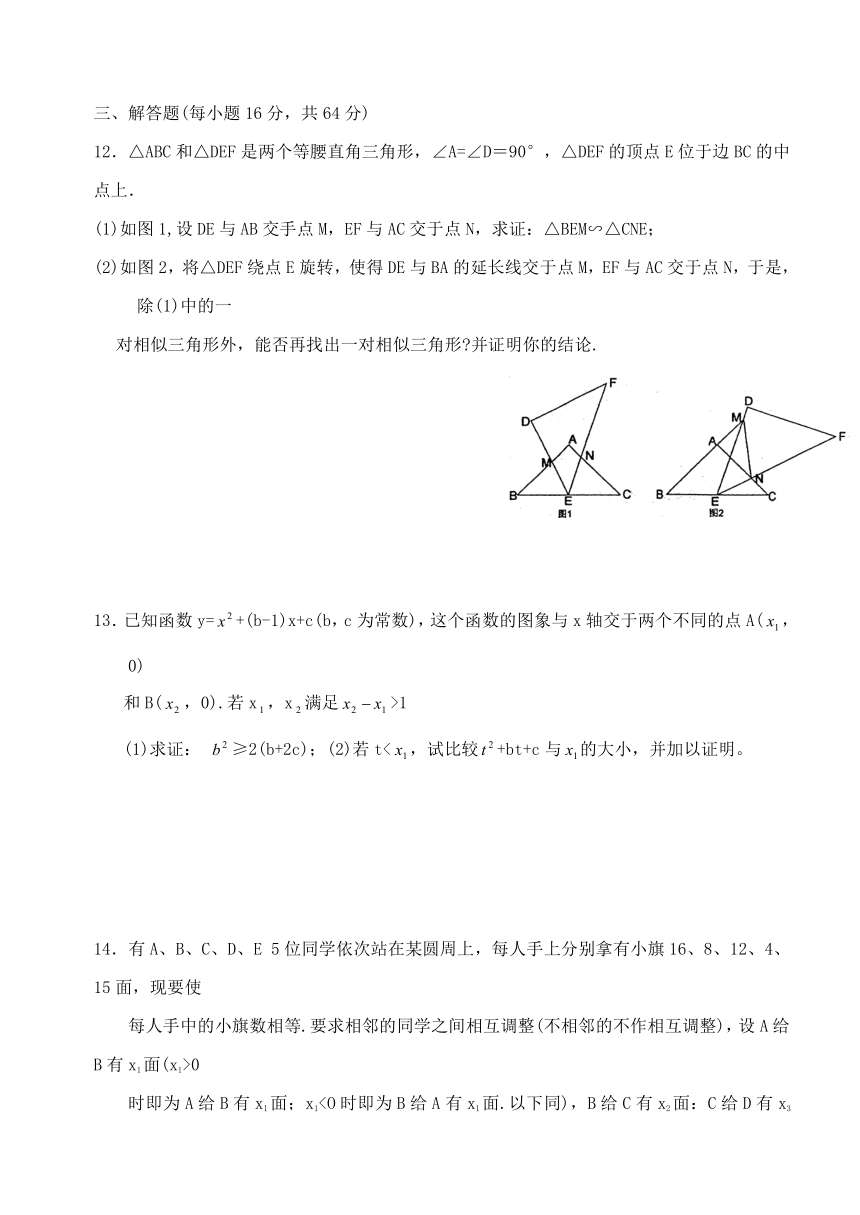
12．△ABC和△DEF是两个等腰直角三角形，∠A=∠D＝90°，△DEF的顶点E位于边BC的中点上．
(1)如图1,设DE与AB交手点M，EF与AC交于点N，求证：△BEM∽△CNE；
(2)如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除(1)中的一
对相似三角形外，能否再找出一对相似三角形 并证明你的结论.
13．已知函数y=+(b-1)x+c(b，c为常数)，这个函数的图象与x轴交于两个不同的点A(，0)
和B(，0).若x，x满足>1
(1)求证： ≥2(b+2c)；(2)若t<，试比较+bt+c与的大小，并加以证明。
14．有A、B、C、D、E 5位同学依次站在某圆周上，每人手上分别拿有小旗16、8、12、4、15面，现要使
每人手中的小旗数相等.要求相邻的同学之间相互调整(不相邻的不作相互调整)，设A给B有x1面(x1>0
时即为A给B有x1面；x1面,E给A有x5面，问x1、x2、x3、x4、x5分别为多少时才能使调动的小旗总数|x1|+|x2|+|x3|+|x4|+|x5|
最小 如图：已知a为正常数，F1(-，0),F2(，0),过F2作直线l，点A，B在直
线l上，且满足AF1-AF2=BF1-BF2=2a，M，N分别为△AF1F2，△BF1F2的内切圆的圆心．
(1)设⊙M与F1F2相切于点P1，⊙N与F1F2切于点P2，试判断P1与P2的位置关系，并加以证明；
(2)已知sin∠BF2F1=8/9，且MN=9/2，试求a的值
[参考答案]
一、选择题(每题6分,共30分)
1．D 2．C．3．A 4．A 5．C
二、填空题(每题6分：共36分)
6．x>-8 7．6 8．(2，2)或(3，)或(-1，)(全部正确才给分)
9．23 10．41 11．甲
三、解答题(共64分)
12．(16分)证：(1)△ABC是等腰直角三角形，
∴∠MBE=45°．
∴∠BME+∠MEB=135°(2分)
又∵△DEF是等腰直角三角形，
∴∠DEF=45°
∴∠NEC+∠MEB=135°，
∴∠BME=∠NEC，(4分)
而∠MBE=∠ECN=45°，
∴△BEM∽△CNE (6分)
(2)与(1)同理△BEM∽△CNE，
BE /CN=EM/NE (10分)
又∵BE=EC．(12分)
∴EC/CN=EM/NE则△ECN与△MEN中EC/CN＝ME/EN，又∠ECN=∠MEN=45°
∴△ECN∽△MEN (16分)
(如给出答案△MBE∽△MEN，同样给相应的分值)
13．(16分)．证：(1)：由已知：x1，2=,又x2-x1>1,(3分)
∴，∴b2-2b+1-4c>1即b2>2(b+2c)。(5分)
(2)由已知x2+(b-1)x+c=(x-x1)(x-x2) (8分)
∴x2+bx+c=(x-x1)(x-x2)+x ，∴t2+bt+c=(t-x1)(t-x2)+t(12分)
t2+bt+c-x1=(t-x1)(t-x2)+t-x1=(t-x1)(t-x2+1) ，∵t1
∴t0 (15分)，即t2+bt+c>x1(16分)
14．(16分)解：∵共有小旗面数；16+8+12+4+15=55面，要使每人手中的小旗面数相等，每人均为11面．
由题意： ∴
∴|x1|+|x2|+|x3|+x4|+|x5|=|x2+3|+|x2|+|x2+1|+|x2-6|+|x2-2|=|x2+3|+|x2+1|+|x2|+|x2-2|+| x2-6|(6分)
设实数x2在数轴上的对应点为P
实数-3，-1，0，2，6在数轴上的对应点分别为P1，P2，P3，P4，P5
∴|x1|+|x2|+|x3|+x4|+|x5|=|PP1|+|PP2|+|PP3|+|PP4|+|PP5|(10分)
当且仅当P在线段P1P5上时|PP1|+|PP5|有最小值9：
当且仅当P在线段P2P4上时|PP2|+|PP4|有最小值3：
当且仅当P与点P3重合时|PP3|有最小值0(14分)
即当且仅当P与点P3重合(x2=0)时
x1+x2+x3+x4+x5=|PP1|+|PP2|+|PP3|+|PP4|+|PP5|有最小值12。
当x1=3，x2=0，x3=1，x4=-6，x5=-2时|x1|+|x2|+|x3|+|x4|+|x5 |有最小值12(16分)
15．(16分)证：(1)由题意：AC=AD，∵AF1-AF2=2a，∴CF1-DF2=2a，又F1C=F1P1 F2D=F2P1
∴P1F1-P1F2=2a (2分)，同理P2F1-P2F2=2a ，∴P1与P2重合(3分)
(2)由(1)知：MP1⊥F1F2，NP2⊥F1F2，P1,P2重合．
∴M，P1，N共线，且MN⊥F1F2(5分)．
连接MN，NE，MD，则∠NED=∠MDE=90°
过N作NH⊥MD，H为垂足，
∵∠MP1F2＝∠MDF2=90°．∠HMN=∠BF2F1(9分)
∴sin∠HMN=sin∠BF2F1=8/9
又MN=9/2
∴NH=MNsin∠HMN=4
∴ED=4．(11分)．
而DF2=F2P1=F2E
∴F2P1=2(14分)
又由(1)P1F1-P1F2=2a．∴P1F1=2+2a
∴P1F1+P1F2=2+2+2a=2(15分)
解得：a=4……(16分)