人教版数学8年级上册 14.2.1 平方差公式 学案(含答案)
文档属性
| 名称 | 人教版数学8年级上册 14.2.1 平方差公式 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 10:40:11 | ||
图片预览


文档简介
平方差公式
班级: 组号: 姓名:
一、旧知回顾
1.多项式乘多项式的法则是什么?
2.运用法则计算下列多项式的积。
(1); (2)。
二、新知梳理
3.请你观察一下回顾旧知的第2题两个多项式与多项式相乘的式子,两个因式有什么特点?积有什么特点?
你能用字母表示这一特点吗? 。
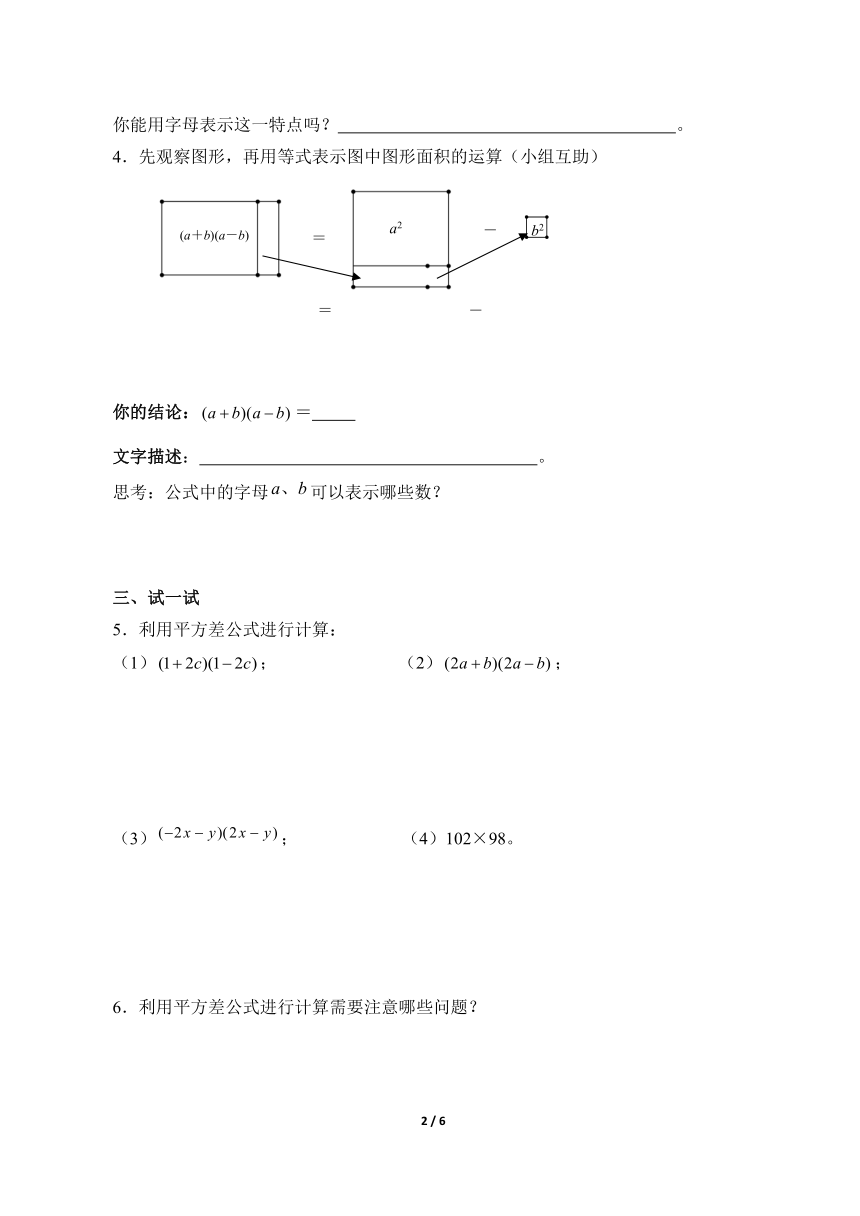
4.先观察图形,再用等式表示图中图形面积的运算(小组互助)
你的结论:=
文字描述: 。
思考:公式中的字母可以表示哪些数?
三、试一试
5.利用平方差公式进行计算:
(1); (2);
; (4)102×98。
6.利用平方差公式进行计算需要注意哪些问题?
★通过预习你还有什么困惑?
一、课堂活动、记录
1.平方差公式的形式与推导。
2.利用平方差公式进行计算需要注意的问题。
二、精练反馈
A组:
1.计算:
(1); (2)。
B组:
2.计算:
(1); (2)999×1001。
思考:
1.你的方法和同桌的方法一样吗?如果不一样,谁的方法更好?
2.利用平方差公式应注意什么?
三、课堂小结
1.本节你掌握了哪些知识?
2.平方差公式有什么结构特征?
四、拓展延伸(选做题)
1.= 。
2.(2+1)(2+1)(2+1)…(2+1)。
已知,求()的值。
【答案】
【学前准备】
1.多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加。
2.(1)原式= (2)原式=
3.答:左边是二项式×二项式,两个二项式中有相同项和相反项,右边为相同项的平方减去相反项的平方。
4.
两数和与两数差的积等于两数的平方差
5.(1)= (2)=
= =
(3)= (4)=(100+2)(100-2)
= =
=9996
6.①有公因式的先提公因式 ②要分到每个多项式不能再因式分解为止。
【课堂探究】
课堂活动、记录
略
精练反馈
1.(1)= (2)=
= =
2.(1)= (2)=(1000-1)(1000+1)
= =
=999999
课堂小结
略
拓展延伸
1.
2.
3.由已知
所以:
5 / 6
班级: 组号: 姓名:
一、旧知回顾
1.多项式乘多项式的法则是什么?
2.运用法则计算下列多项式的积。
(1); (2)。
二、新知梳理
3.请你观察一下回顾旧知的第2题两个多项式与多项式相乘的式子,两个因式有什么特点?积有什么特点?
你能用字母表示这一特点吗? 。
4.先观察图形,再用等式表示图中图形面积的运算(小组互助)
你的结论:=
文字描述: 。
思考:公式中的字母可以表示哪些数?
三、试一试
5.利用平方差公式进行计算:
(1); (2);
; (4)102×98。
6.利用平方差公式进行计算需要注意哪些问题?
★通过预习你还有什么困惑?
一、课堂活动、记录
1.平方差公式的形式与推导。
2.利用平方差公式进行计算需要注意的问题。
二、精练反馈
A组:
1.计算:
(1); (2)。
B组:
2.计算:
(1); (2)999×1001。
思考:
1.你的方法和同桌的方法一样吗?如果不一样,谁的方法更好?
2.利用平方差公式应注意什么?
三、课堂小结
1.本节你掌握了哪些知识?
2.平方差公式有什么结构特征?
四、拓展延伸(选做题)
1.= 。
2.(2+1)(2+1)(2+1)…(2+1)。
已知,求()的值。
【答案】
【学前准备】
1.多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加。
2.(1)原式= (2)原式=
3.答:左边是二项式×二项式,两个二项式中有相同项和相反项,右边为相同项的平方减去相反项的平方。
4.
两数和与两数差的积等于两数的平方差
5.(1)= (2)=
= =
(3)= (4)=(100+2)(100-2)
= =
=9996
6.①有公因式的先提公因式 ②要分到每个多项式不能再因式分解为止。
【课堂探究】
课堂活动、记录
略
精练反馈
1.(1)= (2)=
= =
2.(1)= (2)=(1000-1)(1000+1)
= =
=999999
课堂小结
略
拓展延伸
1.
2.
3.由已知
所以:
5 / 6
