【高分突破】2015年广州版初中数学中考复习课件 第20节 多边形与平行四边形
文档属性
| 名称 | 【高分突破】2015年广州版初中数学中考复习课件 第20节 多边形与平行四边形 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-30 00:00:00 | ||
图片预览






文档简介
课件28张PPT。第20节 多边形与平行四边形★中考导航★两组对边两组对边★考点梳理★两组对角互相平分分别相等平行且相等互相平分★课前预习★1. (2014?梅州)内角和与外角和相等的多边形的边数为 .解析:
设这个多边形是n边形,
则(n﹣2)?180°=360°,
解得n=4.
答案:四.2.在下列四组多边形地板砖中,①正三角形与正方形;②正三角形与正六边形;③正六边形与正方形;④正八边形与正方形.将每组中的两种多边形结合,能密铺地面的是( )
A.①③④ B.②③④C.①②③ D.①②④解析:(1)正三角形内角为60°,正方形内角为90°,可以由3个正三角形和2个正方形可以密铺;(2)正六边形内角120°,可由2个正三角形2个正六边形密铺;(3)正六边形和正方形无法密铺;(4)正八边形内角为135°,正方形内角为90°,2个正八边形和1个正方形可以密铺.答案D.3. (2014?河南)如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
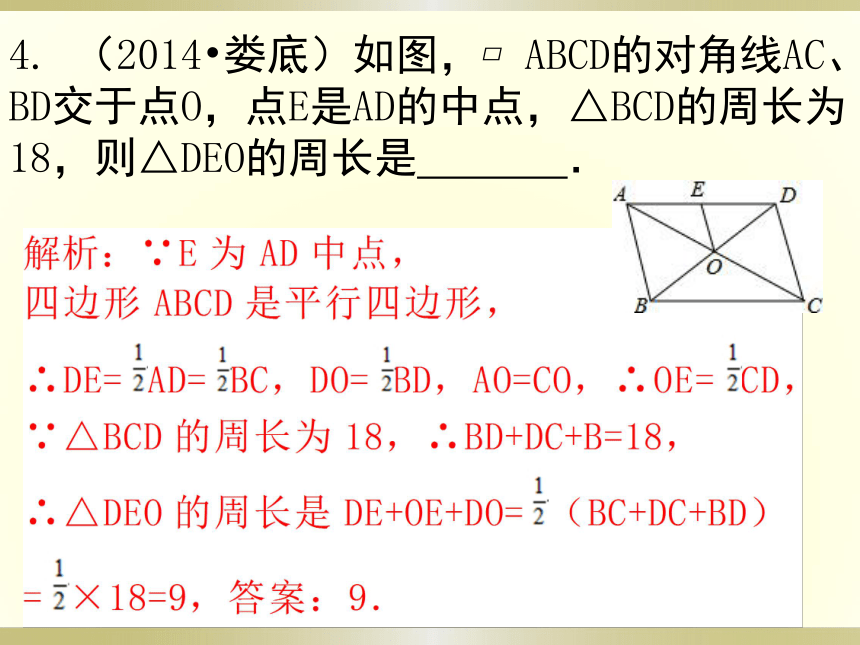
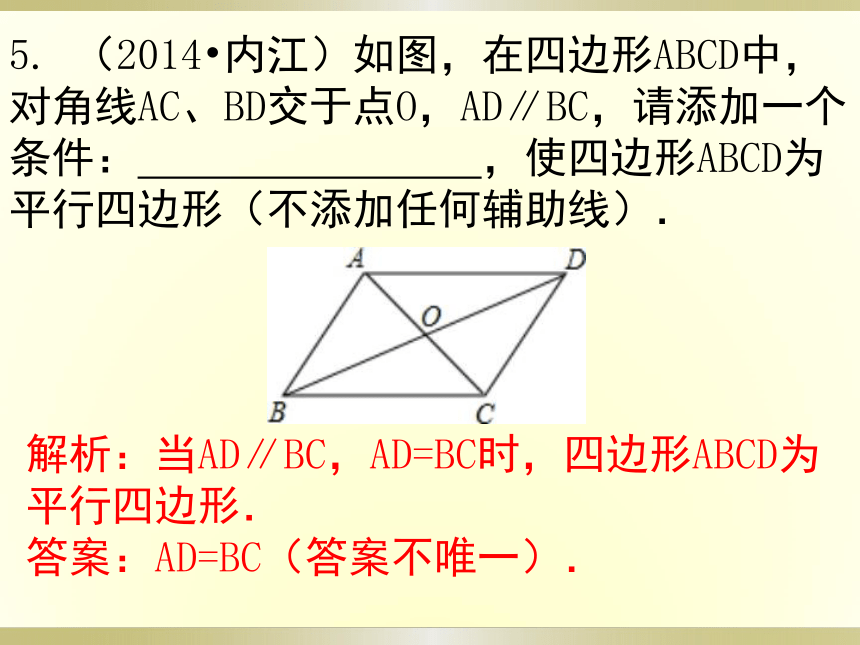
A.8 B.9 C.10 D.114. (2014?娄底)如图,?ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是 .5. (2014?内江)如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: ,使四边形ABCD为平行四边形(不添加任何辅助线).解析:当AD∥BC,AD=BC时,四边形ABCD为平行四边形. 答案:AD=BC(答案不唯一).考点1 多边形的内角和与外角和、平面密铺与镶嵌(★★)
母题集训
1. (2013广东)一个六边形的内角和是 .解析:由内角和公式可得:(6﹣2)×180°=720°.
答案:720°.★考点突破★2. (2009广州)只用下列正多边形地砖中的一种,能够铺满地面的是( )
A. 正十边形 B.正八边形
C. 正六边形 D.正五边形解析:由平面镶嵌的知识可知,只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形,
故选项A、B、D不能够铺满地面.
答案:C.中考预测
3.七边形的内角和为 度,外角和为
度.解析:(7﹣2)?180=900度,外角和为360度.
答案:900;360.
规律总结:n边形的内角和是(n﹣2)?180°,任何多边形的外角和是360度.4.如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A.正三角形 B.正四边形
C.正六边形 D.正八边形解析:A.正三角形的一个内角度数为180°-360°÷3=60°,是360°的约数,能镶嵌平面,不符合题意;B.正四边形的一个内角度数为180°-360°÷4=90°,是360°的约数,能镶嵌平面,不符合题意;C.正六边形的一个内角度数为180°-360°÷6=120°,是360°的约数,能镶嵌平面,不符合题意;D.正八边形的一个内角度数为180°-360°÷8=135°,不是360°的约数,不能镶嵌平面,符合题意;答案:D.考点归纳:本考点曾在2009年广州市中考考查,为次高频考点.考查难度中等,为中等难度题,解答的关键是理解相关概念.本考点应注意掌握的知识点:
正多边形镶嵌有三个条件限制:①边长相等;②顶点公共;③在一个顶点处各正多边形的内角之和为360°.判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能.考点2 平行四边形的性质(★★)
母题集训
1. (2011广州)已知?ABCD的周长为32,AB=4,则BC=( )
A.4 B.12 C.24 D.28解析:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是32,
∴2(AB+BC)=32,
∴BC=12.
答案:B.2. (2010深圳)如图所示,在?ABCD中,AB=5,AD=8,DE平分∠ADC,则BE= .解析:在ABCD中,AB=5,AD=8,
∴BC=8,CD=5,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
又?ABCD中,AD∥BC,
∴∠ADE=∠DEC,
∴∠DEC=∠CDE,∴CD=CE=5,
∴BE=BC﹣CE=8﹣5=3.答案:3.3. 如图,△ABC中,AB=AC=15,D在BC边上,DE∥BA于点E,DF∥CA交AB于点F,那么四边形AFDE的周长是( )
A.30 B.25 C.20 D.15解析:∵AB=AC=15,∴∠B=∠C,
由DF∥AC,得∠FDB=∠C=∠B,
∴FD=FB,
同理,得DE=EC.
∴四边形AFDE的周长=AF+AE+FD+DE
=AF+FB+AE+EC=AB+AC=15+15=30.
答案A.4. 如图,平行四边形ABCD中,AE平分∠BAD.若∠D=110°,则∠DAE的度数为 .考点归纳:本考点曾在2011年广州市中考考查,为次高频考点.考查难度中等,为中等难度题,解答的关键是掌握平行四边形的性质.本考点应注意掌握的知识点:
平行四边形性质的应用通常是通过作对角线把证明平行四边形中的线段、角相等的问题转化为证明三角形全等的问题来处理.考点3 平行四边形的判定(★★)
母题集训
1. (2009广州)如图,在△ABC中,D、E、F分别为边AB、BC、CA的中点.
证明:四边形DECF是平行四边形.解析:连接OC,容易根据已知条件证明四边形ODCE是矩形,然后利用其对角线互相平分和DG=GH=HE可以知道四边形CHOG的对角线互相平分,从而判定其是平行四边形.
答案:证明:连接OC交DE于M.
由矩形得OM=CM,EM=DM.
∵DG=HE.
∴EM﹣EH=DM﹣DG.
∴HM=GM.
∴四边形OGCH是平行四边形.
?中考预测
3.如图,E、F分别是矩形ABCD的边AD、BC上的点,且AE=CF.求证:四边形EBFD为平行四边形.解析:由题意易得ED∥BF,AD=BC而AE=CF,那么可得到ED=BF,即可求证.
答案:证明:∵ABCD为矩形,
∴AD∥BC且AD=BC.
又∵AE=CF,
∴AD﹣AE=BC﹣CF,
即ED=BF,
由ED∥BF且ED=BF,
得四边形EBFD为平行四边形.
(一组对边平行且相等的四边形为平行四边形).4. 已知,如图,在?ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN. (1)求证:△AEM≌△CFN; (2)求证:四边形BMDN是平行四边形.考点归纳:本考点曾在2008~2009年广州市中考考查,为次高频考点.考查难度中等,为中等难度题,解答的关键是掌握平行四边形的判定方法.本考点应注意掌握的知识点:
合理选择平行四边形的判定方法:根据平行四边形的性质可知,利用平行四边形的性质是证明边角相等的有效途径之一,因此,解题时往往先判定一个四边形是平行四边形,然后再利用性质解决问题,至于使用哪种判定方法应依据题目条件灵活确定.
设这个多边形是n边形,
则(n﹣2)?180°=360°,
解得n=4.
答案:四.2.在下列四组多边形地板砖中,①正三角形与正方形;②正三角形与正六边形;③正六边形与正方形;④正八边形与正方形.将每组中的两种多边形结合,能密铺地面的是( )
A.①③④ B.②③④C.①②③ D.①②④解析:(1)正三角形内角为60°,正方形内角为90°,可以由3个正三角形和2个正方形可以密铺;(2)正六边形内角120°,可由2个正三角形2个正六边形密铺;(3)正六边形和正方形无法密铺;(4)正八边形内角为135°,正方形内角为90°,2个正八边形和1个正方形可以密铺.答案D.3. (2014?河南)如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.114. (2014?娄底)如图,?ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是 .5. (2014?内江)如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: ,使四边形ABCD为平行四边形(不添加任何辅助线).解析:当AD∥BC,AD=BC时,四边形ABCD为平行四边形. 答案:AD=BC(答案不唯一).考点1 多边形的内角和与外角和、平面密铺与镶嵌(★★)
母题集训
1. (2013广东)一个六边形的内角和是 .解析:由内角和公式可得:(6﹣2)×180°=720°.
答案:720°.★考点突破★2. (2009广州)只用下列正多边形地砖中的一种,能够铺满地面的是( )
A. 正十边形 B.正八边形
C. 正六边形 D.正五边形解析:由平面镶嵌的知识可知,只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形,
故选项A、B、D不能够铺满地面.
答案:C.中考预测
3.七边形的内角和为 度,外角和为
度.解析:(7﹣2)?180=900度,外角和为360度.
答案:900;360.
规律总结:n边形的内角和是(n﹣2)?180°,任何多边形的外角和是360度.4.如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A.正三角形 B.正四边形
C.正六边形 D.正八边形解析:A.正三角形的一个内角度数为180°-360°÷3=60°,是360°的约数,能镶嵌平面,不符合题意;B.正四边形的一个内角度数为180°-360°÷4=90°,是360°的约数,能镶嵌平面,不符合题意;C.正六边形的一个内角度数为180°-360°÷6=120°,是360°的约数,能镶嵌平面,不符合题意;D.正八边形的一个内角度数为180°-360°÷8=135°,不是360°的约数,不能镶嵌平面,符合题意;答案:D.考点归纳:本考点曾在2009年广州市中考考查,为次高频考点.考查难度中等,为中等难度题,解答的关键是理解相关概念.本考点应注意掌握的知识点:
正多边形镶嵌有三个条件限制:①边长相等;②顶点公共;③在一个顶点处各正多边形的内角之和为360°.判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能.考点2 平行四边形的性质(★★)
母题集训
1. (2011广州)已知?ABCD的周长为32,AB=4,则BC=( )
A.4 B.12 C.24 D.28解析:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是32,
∴2(AB+BC)=32,
∴BC=12.
答案:B.2. (2010深圳)如图所示,在?ABCD中,AB=5,AD=8,DE平分∠ADC,则BE= .解析:在ABCD中,AB=5,AD=8,
∴BC=8,CD=5,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
又?ABCD中,AD∥BC,
∴∠ADE=∠DEC,
∴∠DEC=∠CDE,∴CD=CE=5,
∴BE=BC﹣CE=8﹣5=3.答案:3.3. 如图,△ABC中,AB=AC=15,D在BC边上,DE∥BA于点E,DF∥CA交AB于点F,那么四边形AFDE的周长是( )
A.30 B.25 C.20 D.15解析:∵AB=AC=15,∴∠B=∠C,
由DF∥AC,得∠FDB=∠C=∠B,
∴FD=FB,
同理,得DE=EC.
∴四边形AFDE的周长=AF+AE+FD+DE
=AF+FB+AE+EC=AB+AC=15+15=30.
答案A.4. 如图,平行四边形ABCD中,AE平分∠BAD.若∠D=110°,则∠DAE的度数为 .考点归纳:本考点曾在2011年广州市中考考查,为次高频考点.考查难度中等,为中等难度题,解答的关键是掌握平行四边形的性质.本考点应注意掌握的知识点:
平行四边形性质的应用通常是通过作对角线把证明平行四边形中的线段、角相等的问题转化为证明三角形全等的问题来处理.考点3 平行四边形的判定(★★)
母题集训
1. (2009广州)如图,在△ABC中,D、E、F分别为边AB、BC、CA的中点.
证明:四边形DECF是平行四边形.解析:连接OC,容易根据已知条件证明四边形ODCE是矩形,然后利用其对角线互相平分和DG=GH=HE可以知道四边形CHOG的对角线互相平分,从而判定其是平行四边形.
答案:证明:连接OC交DE于M.
由矩形得OM=CM,EM=DM.
∵DG=HE.
∴EM﹣EH=DM﹣DG.
∴HM=GM.
∴四边形OGCH是平行四边形.
?中考预测
3.如图,E、F分别是矩形ABCD的边AD、BC上的点,且AE=CF.求证:四边形EBFD为平行四边形.解析:由题意易得ED∥BF,AD=BC而AE=CF,那么可得到ED=BF,即可求证.
答案:证明:∵ABCD为矩形,
∴AD∥BC且AD=BC.
又∵AE=CF,
∴AD﹣AE=BC﹣CF,
即ED=BF,
由ED∥BF且ED=BF,
得四边形EBFD为平行四边形.
(一组对边平行且相等的四边形为平行四边形).4. 已知,如图,在?ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN. (1)求证:△AEM≌△CFN; (2)求证:四边形BMDN是平行四边形.考点归纳:本考点曾在2008~2009年广州市中考考查,为次高频考点.考查难度中等,为中等难度题,解答的关键是掌握平行四边形的判定方法.本考点应注意掌握的知识点:
合理选择平行四边形的判定方法:根据平行四边形的性质可知,利用平行四边形的性质是证明边角相等的有效途径之一,因此,解题时往往先判定一个四边形是平行四边形,然后再利用性质解决问题,至于使用哪种判定方法应依据题目条件灵活确定.
同课章节目录
