3.1.3倍角的正弦,余弦,正切公式_教学设计(表格式)
文档属性
| 名称 | 3.1.3倍角的正弦,余弦,正切公式_教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 00:00:00 | ||
图片预览



文档简介
课题 二倍角的正弦、余弦、正切公式
教学目标
教学目标: 1. 了解二倍角的正弦、余弦、正切公式,会运用公式进行简单的三角恒等变换; 2. 经历二倍角公式推导过程,感悟从一般到特殊的研究方法,体会转化和换元的思想; 3. 发展逻辑推理和数学运算的核心素养,培养数学整体观. 教学重点:二倍角的正弦、余弦、正切公式 教学难点:二倍角公式在三角恒等变换中的应用
教学过程
时 间 教学 环节 主要师生活动
复 习 引入 上节课我们由两角差的余弦公式,得到了两角和与差的正弦、余弦、 正切共六个公式,我们一起来回顾一下上一节课具体的探究思路: 我们当时已经得到的是两角差的余弦公式: cos (a -b) = cosa cos b+ sin asin b, 首先我们将两角差的余弦公式中b替换为-b,得到了两角和的余弦公 式:cos (a + b) = cosa cos b- sin asin b, 然后我们为了改变三角函数名,借助诱导公式得到了两角和与差的正 弦公式:sin(a + b) = sin a cos b+ cosasin b; sin(a -b) = sin a cos b- cosasin b, 最后利用同角关系将正切转化为正余弦,得到了两角和与差的正切公
累 计 4 分 钟 探 究 新知 式:tan (a + b) = 1ta- ;tan (a -b) = 1 . 以及上一节课我们也说到,正切的公式使用起来有相应角范围的限制, 也就是正切值都要存在。例如这个两角和的正切公式,要求a,b均不 等于 + kπ(k Z),并且a + b也不等于 + kπ(k Z),如果碰到相 应的情况例如已知tana 去求tan - a ,就不能用两角差的正切公式 了,只能通过同角关系转化回正余弦求解了。 那回顾完之前的内容,今天我们在这六个和角、差角公式的基础上, 来探究倍角公式。 (一)探究二倍角的正弦、余弦、正切公式 我们先来看二倍角的正弦公式 【问题 1.1】我们需要求的sin 2a和已知的sin(a ± b) 公式形式上有什 么联系吗? 我们发现它们都是角的正弦,只是角的形式不同,但不同角的形式从 运算或换元的角度都有内在联系,因此基于差异可以建立联系,进行 转化。 【问题 1.2】你能类比上一节课的探究过程,利用 S(a±b) 公式推导出 sin 2a 的公式吗? 我们比较sin 2a和sin(a ± b) ,注意到2a = a +a ,由于两角和的正弦 公式对任意的a, b 都成立,那么把其中的b换为a 后,也一定成立。 则由公式S(a+b) ,有 sin 2a = sin(a +a) = sin a cosa + cosasin a = 2sin a cosa 刚刚我们的推导过程是借助S(a+b)来完成的,如果用S(a-b)来完成推导 方法也基本相同,把公式中的-b替换为a 即可。 这样我们就得到了二倍角的正弦公式。
这个推导过程实质上是一个从一般到特殊的推导过程,后续这样的方 法在三角恒等变换中非常有用。 【 问 题 1.3 】 你 能 仿 照 刚 刚 的 推 导 过 程 , 利 用 C(a±b) , T(a±b) 得 到 cos 2a, tan 2a 的公式吗? 和刚才一样,我们将cos (a + b) ,tan (a + b)公式中的b换为a 后,得 到: cos 2a = cos (a +a) = cosa cosa - sin asin a = cos2 a - sin2 a tan 2a = tan(a +a) = 1-tatna = 1-2 【问题 1.4】如果要求二倍角的余弦公式中仅含a 的正弦或者余弦,那 么cos 2a还有其它的表示形式吗? 我们可以借助同角关系sin2 a + cos2 a = 1 进行形式上的等价转化: (
2 2
(
2
)
2
2
)cos 2a = cos a - sin a = 1- sin a - sin a = 1- 2sin a cos 2a = cos2 a - sin2 a = cos2 a - (1- cos2 a) = 2 cos2 a - 1 【过渡】以上这些公式都叫做倍角公式. 倍角公式给出了a 的三角函 数与2a的三角函数之间的关系. 特别注明:上面说的“倍角 ”专指“二倍角 ”,遇到“三倍角 ”等名词 时,不能省略. 【问题 1.5】由二倍角的余弦公式我们看到,已知sin a 或者cosa 可以 求出cos 2a 的值,那么已知cos 2a时,是否能够反向求出sin a 和cosa 呢? 我们可以通过方程的的角度看二倍角的余弦公式,有下面的等价形式: 1+ cos 2a = 2 cos2 a 即cos2 a = 1- cos 2a = 2 sin2 a 即sin2 a = sin a 与cosa 的符号由角a 的范围确定. 刚刚这两个公式的变形我们从左向右看,角之间是倍角关系,从结构
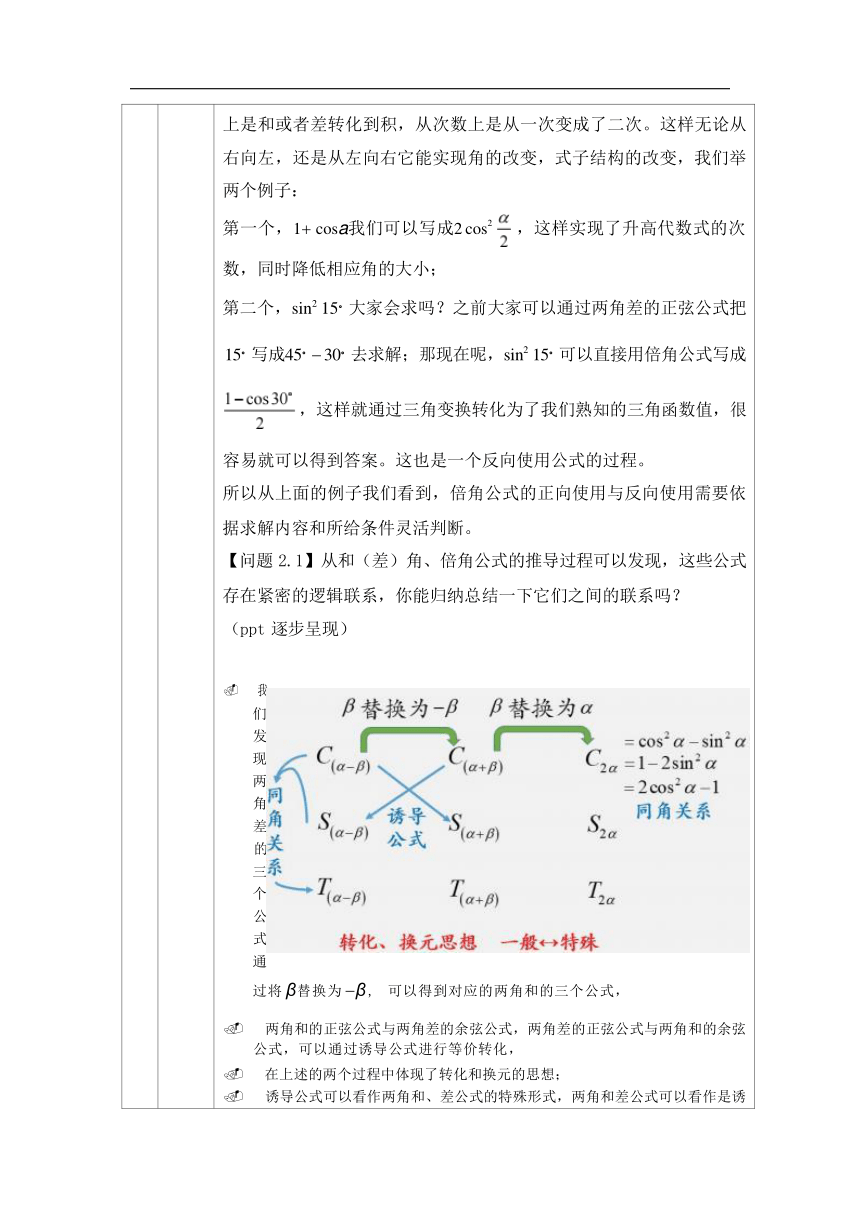
上是和或者差转化到积,从次数上是从一次变成了二次。这样无论从 右向左,还是从左向右它能实现角的改变,式子结构的改变,我们举 两个例子: 第一个,1+ cosa我们可以写成2 cos2 ,这样实现了升高代数式的次 数,同时降低相应角的大小; 第二个,sin2 15。大家会求吗?之前大家可以通过两角差的正弦公式把 15。写成45。- 30。去求解;那现在呢,sin2 15。可以直接用倍角公式写成 ,这样就通过三角变换转化为了我们熟知的三角函数值,很 容易就可以得到答案。这也是一个反向使用公式的过程。 所以从上面的例子我们看到,倍角公式的正向使用与反向使用需要依 据求解内容和所给条件灵活判断。 【问题 2.1】从和(差)角、倍角公式的推导过程可以发现,这些公式 存在紧密的逻辑联系,你能归纳总结一下它们之间的联系吗? (ppt 逐步呈现) . 我 们 发 现 两 角 差 的 三 个 公 式 通 过将 β替换为 -β , 可以得到对应的两角和的三个公式, . 两角和的正弦公式与两角差的余弦公式,两角差的正弦公式与两角和的余弦 公式,可以通过诱导公式进行等价转化, . 在上述的两个过程中体现了转化和换元的思想; . 诱导公式可以看作两角和、差公式的特殊形式,两角和差公式可以看作是诱
累 计 12 分 钟 巩 固 应用 导公式更一般的形式; . 可以将和角公式中的b替换为a ,或者将差角公式中的 b替换为 -a ,得 到对应的倍角公式,这个过程中体现了从一般到特殊的数学思想; . 所有的正切公式都可以利用相同角的正余弦公式通过同角关系得到; . 二倍角的余弦公式的三种等价表达形式可以通过同角关系互相推导. (二)二倍角的正弦、余弦、正切公式的初步应用
【例 1】已知sin 2a = (
π
4
) 5 , 13 < a < , 求sin 4a ,cos 4a ,tan 4a 的值.
分析:我们观察到4a是2a的二倍角,因此可以考虑用倍角公式求解 接下来我们设计一下解决问题的路径: 根据二倍角的正弦公式,sin 4a = 2sin 2a cos 2a,因此只需通过同角关 系由sin 2a求出cos 2a 即可,cos 2a 的符号通过角的范围确定; cos 4a = 1- 2sin2 2a ,可以直接求出值; tan 4a 既可以通过同角关系= 计算;也可用 求出tan 2a , 再利用二倍角的正切公式求解.
解 : 由 < a < π , 2 得 < 2a < π , 又 sin 2a = 5 , 13 所 以
(
cos 2
a
= -
1
-
è
13
÷
= -
13
.
) 5 2 12 于是sin 4a = sin2 (2a) = 2sin 2a cos 2a = 2 1 - = - cos 4a = cos 2 (2a) = 1- 2sin2 2a = 1- 2 2 = tan 4a = = - = - (或tan 2a = = 1 - = - 1 ,
tan 4a = tan2 (2a) = 1 = 12- è--1 = - ) 【问题 3.1】通过这道例题,你对倍角公式中的“倍 ”有更深入的理解 吗? 我们从这道例题中发现,“倍 ”是描述两个数量之间关系的,2a是a 的 二倍,4a是2a的二倍, 是 的二倍,这里蕴含着换元思想. 【例 2】在△ ABC 中,cos A = ,tan B = 2 ,求tan (2A + 2B)的值. 分析:这道题要求tan (2A + 2B) 的值,我们可以拆分为求解tan 2A 和 tan 2B 的值,再用正切两角和的公式就可以求出答案。tan 2A 和tan 2B 相比我们已知的cos A 和tan B 虽然三角函数名不尽相同,但角是二倍 的关系,所以我们可以考虑用倍角公式求解,涉及到符号的确定借助
三角形内角在(0, π ) 的范围即可. 解 法 1 : 在 △ ABC 中 , 由 cos A = 4 5 , 0 < A < π , 得
(
3
=
5
) (
1
-
cos
2
A
=
) (
sin
A
=
) (
1
-
2
) (
tan
2
A
=
) 2 tan A 2 24 = = 1 - tan2 A 1 - 2 7 (
tan
2
B
=
) 2 tan B 2 2 4 = = - 1- tan2 B 1- 22 3 , 所 以 tan A = = , 又tan B = 2 ,所以 = ,
于是tan (2A + 2B) = tan 2A + tan 2B = 1 - tan 2Atan 2B 24 4 7 3 44 = 1 - - 117
【问题 3.2】刚刚我们从已知的cos A 和tan B ,求出了tan 2A 和tan 2B ,
最后得到了题目中要求的tan (2A + 2B) 。那请大家思考,这道题目还有 其他能够解决问题的方法吗? 我们可以把要求的tan (2A + 2B) 看成tan 2 (A + B) ,也就是角A 与角 B 和的二倍角的正切值,那么可以设计出下面的路径: 由cos A 和tan B 统一三角函数名得到tan A 和tan B ,然后利用两角和的 正 切 公 式 得 到 tan (A + B) , 最 后 通 过 二 倍 角 公 式 得 到 所 需 的
tan (2A + 2B) .具体过程我们一起来看: 解 法 2 : 在 △ ABC 中 , 由 cos A = 4 5 , 0 < A < π , 3 , 4 得 又
(
sin
A
=
) (
=
) (
1
-
cos
2
A
) tan B = 2 , (
1
-
2
) 3 (
=
), 5 所以 tan A = = =
所以tan (A + B) = 1tt = 1 -43 2 = - , 所以
tan (2A + 2B) = tan 2 (A + B ) = 1) = 12- -- = 1 我们看到,解法 2 相比解法 1 少了一个运算步骤,但它们都是对倍角、 和角关系的联合运用,只是对角2A + 2B ,与角A, B 之间关系的看法不 同,或者说计算顺序不同,本质上没有区别。 同时做完这道题后我们也发现,题干中的“在△ ABC 中 ”隐含了 0 < A < π 的条件,这类在三角形中隐含的条件值得同学们进行总结. 【小结】 这节课我们从之前得到的六个两角和与差的正弦、余弦、正切公式入 手,通过转化与换元的方法得到了二倍角的正弦、余弦、正切公式,
累 计 19 分 钟 累 计 21 分 钟 课 堂 小结 借助同角关系发现了余弦二倍角公式的三个等价形式,并且探究了这 节课与之前共 11 个三角变换的公式之间的逻辑联系,然后应用倍角公 式解决了几个实际的问题。 在解决问题的过程中我们发现: 倍角公式的“倍 ”代表了一种数量关系,并不只是2a与a ,只要符合 这种角关系的问题都可以考虑应用倍角公式; 在三角函数名与角之间,我们应当先关注所求角与已知角之间的关系, 并以此来设计解决问题的方法,三角函数名可以通过同角关系进行转 化; 倍角公式相比两角和差的公式形式上更简洁,多样,并且由于“倍 ” 的相对性决定了它既是倍角公式,也是半角公式,是一个桥梁纽带的 作用,所以在解决问题过程中两角和与差的公式与二倍角公式不是割 裂开的,连同公式正向与反向使用都应当依据所需进行选取,灵活应 用解决问题。 至于如何分析对比变换目标,如何选择公式,如何根据问题条件进行 变形,就留到下一节课再和大家探讨。
教学目标
教学目标: 1. 了解二倍角的正弦、余弦、正切公式,会运用公式进行简单的三角恒等变换; 2. 经历二倍角公式推导过程,感悟从一般到特殊的研究方法,体会转化和换元的思想; 3. 发展逻辑推理和数学运算的核心素养,培养数学整体观. 教学重点:二倍角的正弦、余弦、正切公式 教学难点:二倍角公式在三角恒等变换中的应用
教学过程
时 间 教学 环节 主要师生活动
复 习 引入 上节课我们由两角差的余弦公式,得到了两角和与差的正弦、余弦、 正切共六个公式,我们一起来回顾一下上一节课具体的探究思路: 我们当时已经得到的是两角差的余弦公式: cos (a -b) = cosa cos b+ sin asin b, 首先我们将两角差的余弦公式中b替换为-b,得到了两角和的余弦公 式:cos (a + b) = cosa cos b- sin asin b, 然后我们为了改变三角函数名,借助诱导公式得到了两角和与差的正 弦公式:sin(a + b) = sin a cos b+ cosasin b; sin(a -b) = sin a cos b- cosasin b, 最后利用同角关系将正切转化为正余弦,得到了两角和与差的正切公
累 计 4 分 钟 探 究 新知 式:tan (a + b) = 1ta- ;tan (a -b) = 1 . 以及上一节课我们也说到,正切的公式使用起来有相应角范围的限制, 也就是正切值都要存在。例如这个两角和的正切公式,要求a,b均不 等于 + kπ(k Z),并且a + b也不等于 + kπ(k Z),如果碰到相 应的情况例如已知tana 去求tan - a ,就不能用两角差的正切公式 了,只能通过同角关系转化回正余弦求解了。 那回顾完之前的内容,今天我们在这六个和角、差角公式的基础上, 来探究倍角公式。 (一)探究二倍角的正弦、余弦、正切公式 我们先来看二倍角的正弦公式 【问题 1.1】我们需要求的sin 2a和已知的sin(a ± b) 公式形式上有什 么联系吗? 我们发现它们都是角的正弦,只是角的形式不同,但不同角的形式从 运算或换元的角度都有内在联系,因此基于差异可以建立联系,进行 转化。 【问题 1.2】你能类比上一节课的探究过程,利用 S(a±b) 公式推导出 sin 2a 的公式吗? 我们比较sin 2a和sin(a ± b) ,注意到2a = a +a ,由于两角和的正弦 公式对任意的a, b 都成立,那么把其中的b换为a 后,也一定成立。 则由公式S(a+b) ,有 sin 2a = sin(a +a) = sin a cosa + cosasin a = 2sin a cosa 刚刚我们的推导过程是借助S(a+b)来完成的,如果用S(a-b)来完成推导 方法也基本相同,把公式中的-b替换为a 即可。 这样我们就得到了二倍角的正弦公式。
这个推导过程实质上是一个从一般到特殊的推导过程,后续这样的方 法在三角恒等变换中非常有用。 【 问 题 1.3 】 你 能 仿 照 刚 刚 的 推 导 过 程 , 利 用 C(a±b) , T(a±b) 得 到 cos 2a, tan 2a 的公式吗? 和刚才一样,我们将cos (a + b) ,tan (a + b)公式中的b换为a 后,得 到: cos 2a = cos (a +a) = cosa cosa - sin asin a = cos2 a - sin2 a tan 2a = tan(a +a) = 1-tatna = 1-2 【问题 1.4】如果要求二倍角的余弦公式中仅含a 的正弦或者余弦,那 么cos 2a还有其它的表示形式吗? 我们可以借助同角关系sin2 a + cos2 a = 1 进行形式上的等价转化: (
2 2
(
2
)
2
2
)cos 2a = cos a - sin a = 1- sin a - sin a = 1- 2sin a cos 2a = cos2 a - sin2 a = cos2 a - (1- cos2 a) = 2 cos2 a - 1 【过渡】以上这些公式都叫做倍角公式. 倍角公式给出了a 的三角函 数与2a的三角函数之间的关系. 特别注明:上面说的“倍角 ”专指“二倍角 ”,遇到“三倍角 ”等名词 时,不能省略. 【问题 1.5】由二倍角的余弦公式我们看到,已知sin a 或者cosa 可以 求出cos 2a 的值,那么已知cos 2a时,是否能够反向求出sin a 和cosa 呢? 我们可以通过方程的的角度看二倍角的余弦公式,有下面的等价形式: 1+ cos 2a = 2 cos2 a 即cos2 a = 1- cos 2a = 2 sin2 a 即sin2 a = sin a 与cosa 的符号由角a 的范围确定. 刚刚这两个公式的变形我们从左向右看,角之间是倍角关系,从结构
上是和或者差转化到积,从次数上是从一次变成了二次。这样无论从 右向左,还是从左向右它能实现角的改变,式子结构的改变,我们举 两个例子: 第一个,1+ cosa我们可以写成2 cos2 ,这样实现了升高代数式的次 数,同时降低相应角的大小; 第二个,sin2 15。大家会求吗?之前大家可以通过两角差的正弦公式把 15。写成45。- 30。去求解;那现在呢,sin2 15。可以直接用倍角公式写成 ,这样就通过三角变换转化为了我们熟知的三角函数值,很 容易就可以得到答案。这也是一个反向使用公式的过程。 所以从上面的例子我们看到,倍角公式的正向使用与反向使用需要依 据求解内容和所给条件灵活判断。 【问题 2.1】从和(差)角、倍角公式的推导过程可以发现,这些公式 存在紧密的逻辑联系,你能归纳总结一下它们之间的联系吗? (ppt 逐步呈现) . 我 们 发 现 两 角 差 的 三 个 公 式 通 过将 β替换为 -β , 可以得到对应的两角和的三个公式, . 两角和的正弦公式与两角差的余弦公式,两角差的正弦公式与两角和的余弦 公式,可以通过诱导公式进行等价转化, . 在上述的两个过程中体现了转化和换元的思想; . 诱导公式可以看作两角和、差公式的特殊形式,两角和差公式可以看作是诱
累 计 12 分 钟 巩 固 应用 导公式更一般的形式; . 可以将和角公式中的b替换为a ,或者将差角公式中的 b替换为 -a ,得 到对应的倍角公式,这个过程中体现了从一般到特殊的数学思想; . 所有的正切公式都可以利用相同角的正余弦公式通过同角关系得到; . 二倍角的余弦公式的三种等价表达形式可以通过同角关系互相推导. (二)二倍角的正弦、余弦、正切公式的初步应用
【例 1】已知sin 2a = (
π
4
) 5 , 13 < a < , 求sin 4a ,cos 4a ,tan 4a 的值.
分析:我们观察到4a是2a的二倍角,因此可以考虑用倍角公式求解 接下来我们设计一下解决问题的路径: 根据二倍角的正弦公式,sin 4a = 2sin 2a cos 2a,因此只需通过同角关 系由sin 2a求出cos 2a 即可,cos 2a 的符号通过角的范围确定; cos 4a = 1- 2sin2 2a ,可以直接求出值; tan 4a 既可以通过同角关系= 计算;也可用 求出tan 2a , 再利用二倍角的正切公式求解.
解 : 由 < a < π , 2 得 < 2a < π , 又 sin 2a = 5 , 13 所 以
(
cos 2
a
= -
1
-
è
13
÷
= -
13
.
) 5 2 12 于是sin 4a = sin2 (2a) = 2sin 2a cos 2a = 2 1 - = - cos 4a = cos 2 (2a) = 1- 2sin2 2a = 1- 2 2 = tan 4a = = - = - (或tan 2a = = 1 - = - 1 ,
tan 4a = tan2 (2a) = 1 = 12- è--1 = - ) 【问题 3.1】通过这道例题,你对倍角公式中的“倍 ”有更深入的理解 吗? 我们从这道例题中发现,“倍 ”是描述两个数量之间关系的,2a是a 的 二倍,4a是2a的二倍, 是 的二倍,这里蕴含着换元思想. 【例 2】在△ ABC 中,cos A = ,tan B = 2 ,求tan (2A + 2B)的值. 分析:这道题要求tan (2A + 2B) 的值,我们可以拆分为求解tan 2A 和 tan 2B 的值,再用正切两角和的公式就可以求出答案。tan 2A 和tan 2B 相比我们已知的cos A 和tan B 虽然三角函数名不尽相同,但角是二倍 的关系,所以我们可以考虑用倍角公式求解,涉及到符号的确定借助
三角形内角在(0, π ) 的范围即可. 解 法 1 : 在 △ ABC 中 , 由 cos A = 4 5 , 0 < A < π , 得
(
3
=
5
) (
1
-
cos
2
A
=
) (
sin
A
=
) (
1
-
2
) (
tan
2
A
=
) 2 tan A 2 24 = = 1 - tan2 A 1 - 2 7 (
tan
2
B
=
) 2 tan B 2 2 4 = = - 1- tan2 B 1- 22 3 , 所 以 tan A = = , 又tan B = 2 ,所以 = ,
于是tan (2A + 2B) = tan 2A + tan 2B = 1 - tan 2Atan 2B 24 4 7 3 44 = 1 - - 117
【问题 3.2】刚刚我们从已知的cos A 和tan B ,求出了tan 2A 和tan 2B ,
最后得到了题目中要求的tan (2A + 2B) 。那请大家思考,这道题目还有 其他能够解决问题的方法吗? 我们可以把要求的tan (2A + 2B) 看成tan 2 (A + B) ,也就是角A 与角 B 和的二倍角的正切值,那么可以设计出下面的路径: 由cos A 和tan B 统一三角函数名得到tan A 和tan B ,然后利用两角和的 正 切 公 式 得 到 tan (A + B) , 最 后 通 过 二 倍 角 公 式 得 到 所 需 的
tan (2A + 2B) .具体过程我们一起来看: 解 法 2 : 在 △ ABC 中 , 由 cos A = 4 5 , 0 < A < π , 3 , 4 得 又
(
sin
A
=
) (
=
) (
1
-
cos
2
A
) tan B = 2 , (
1
-
2
) 3 (
=
), 5 所以 tan A = = =
所以tan (A + B) = 1tt = 1 -43 2 = - , 所以
tan (2A + 2B) = tan 2 (A + B ) = 1) = 12- -- = 1 我们看到,解法 2 相比解法 1 少了一个运算步骤,但它们都是对倍角、 和角关系的联合运用,只是对角2A + 2B ,与角A, B 之间关系的看法不 同,或者说计算顺序不同,本质上没有区别。 同时做完这道题后我们也发现,题干中的“在△ ABC 中 ”隐含了 0 < A < π 的条件,这类在三角形中隐含的条件值得同学们进行总结. 【小结】 这节课我们从之前得到的六个两角和与差的正弦、余弦、正切公式入 手,通过转化与换元的方法得到了二倍角的正弦、余弦、正切公式,
累 计 19 分 钟 累 计 21 分 钟 课 堂 小结 借助同角关系发现了余弦二倍角公式的三个等价形式,并且探究了这 节课与之前共 11 个三角变换的公式之间的逻辑联系,然后应用倍角公 式解决了几个实际的问题。 在解决问题的过程中我们发现: 倍角公式的“倍 ”代表了一种数量关系,并不只是2a与a ,只要符合 这种角关系的问题都可以考虑应用倍角公式; 在三角函数名与角之间,我们应当先关注所求角与已知角之间的关系, 并以此来设计解决问题的方法,三角函数名可以通过同角关系进行转 化; 倍角公式相比两角和差的公式形式上更简洁,多样,并且由于“倍 ” 的相对性决定了它既是倍角公式,也是半角公式,是一个桥梁纽带的 作用,所以在解决问题过程中两角和与差的公式与二倍角公式不是割 裂开的,连同公式正向与反向使用都应当依据所需进行选取,灵活应 用解决问题。 至于如何分析对比变换目标,如何选择公式,如何根据问题条件进行 变形,就留到下一节课再和大家探讨。
