5.1.2垂线课件(第2课时)
文档属性
| 名称 | 5.1.2垂线课件(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 556.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-31 07:57:28 | ||
图片预览

文档简介
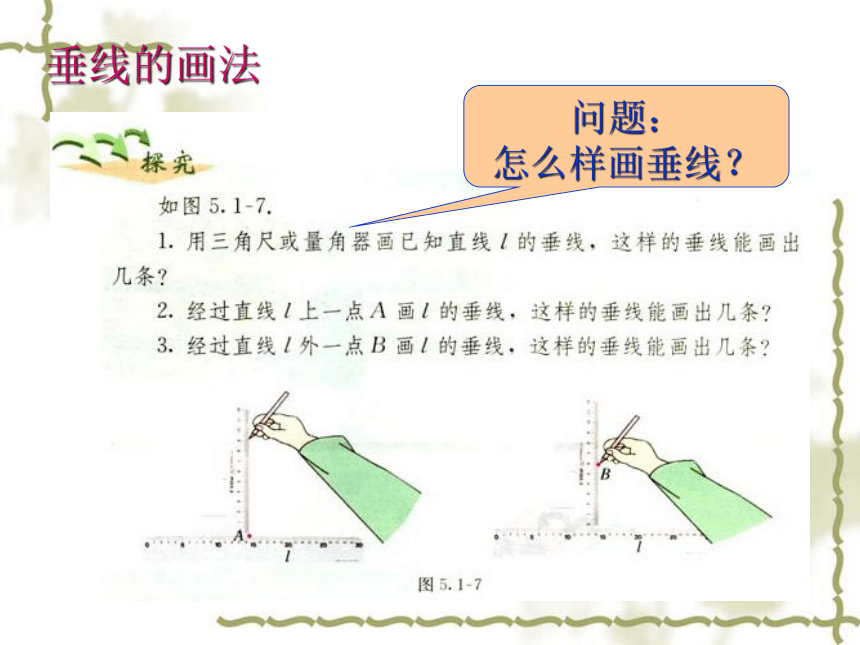
课件27张PPT。5.1.2垂线2问题:
怎么样画垂线?垂线的画法问题:
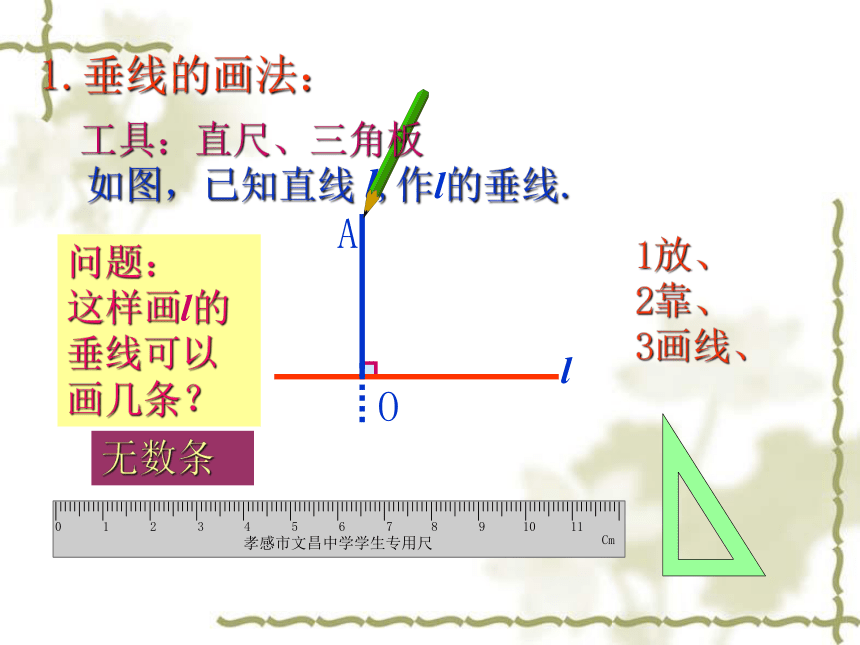
这样画l的垂线可以画几条?1放、
2靠、
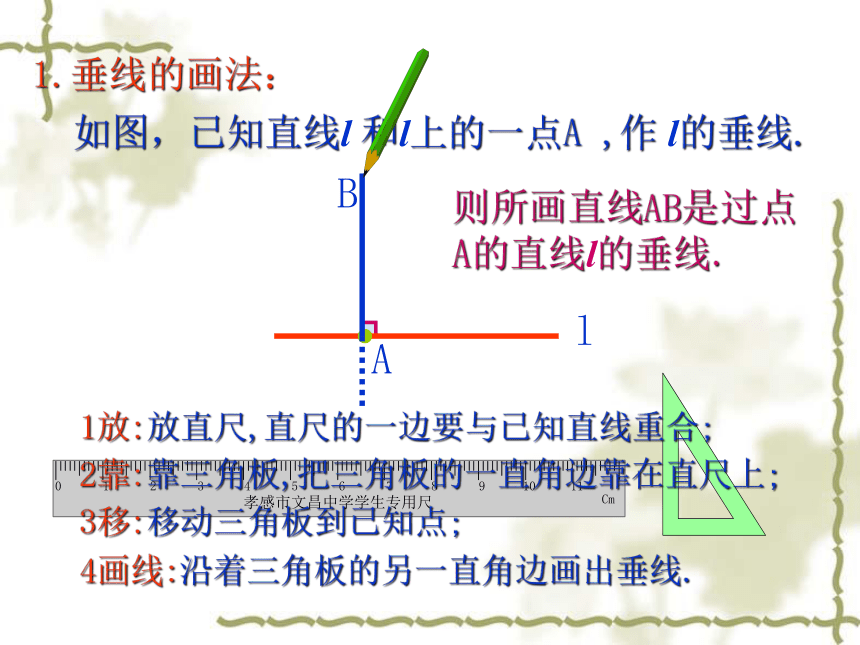
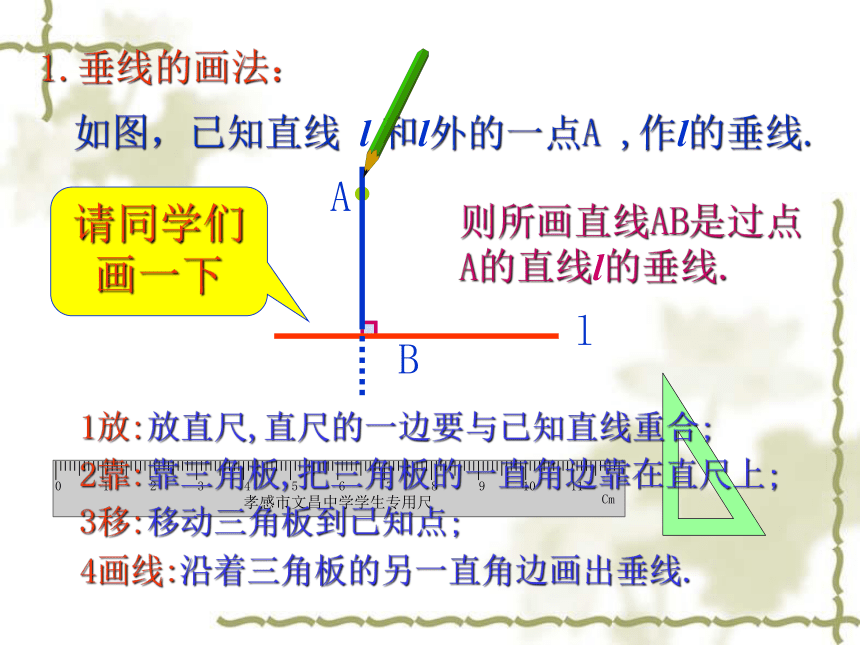
3画线、O如图,已知直线 l,作l的垂线.工具:直尺、三角板A无数条1.垂线的画法:llA如图,已知直线l 和l上的一点A ,作 l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.请同学们画一下1.垂线的画法: 结论:
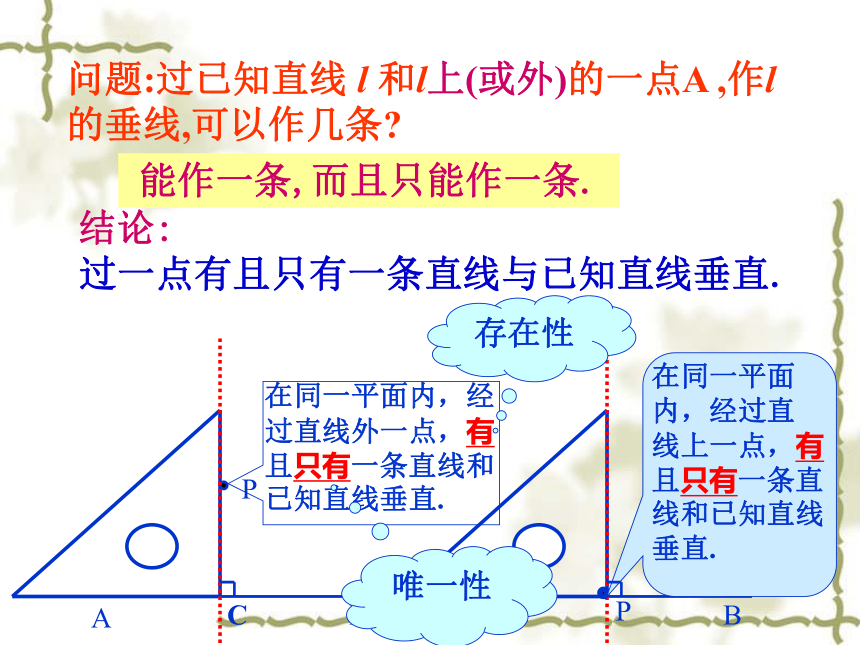
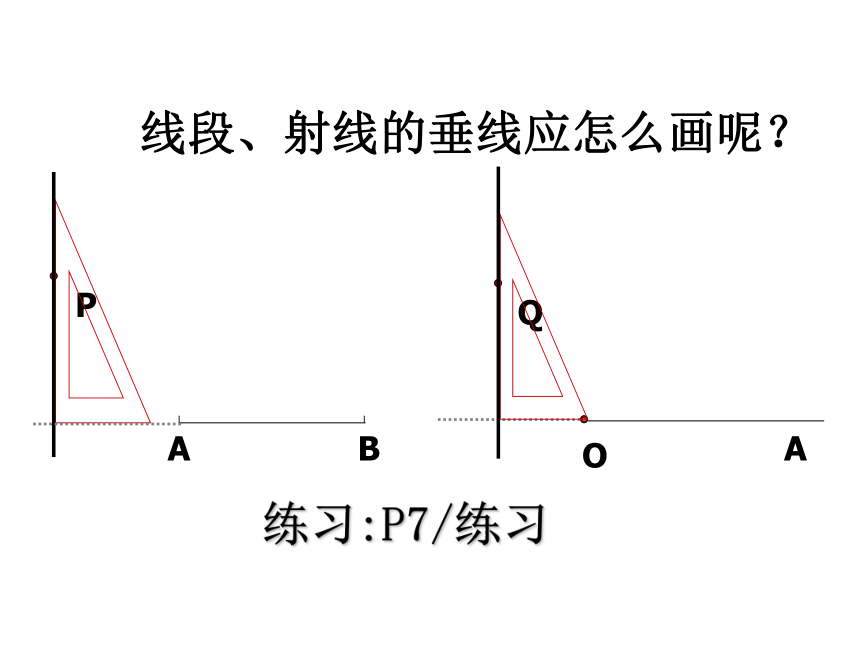
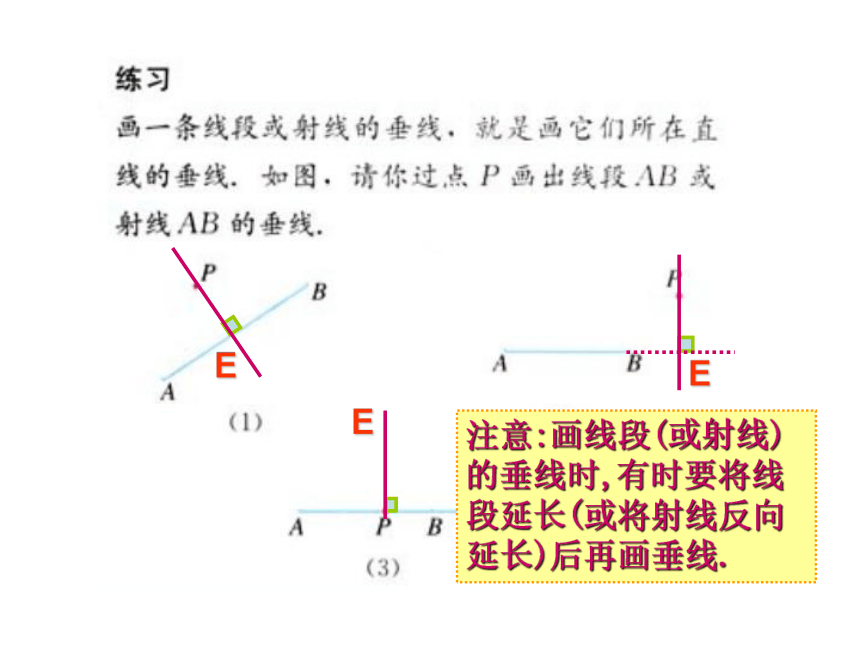
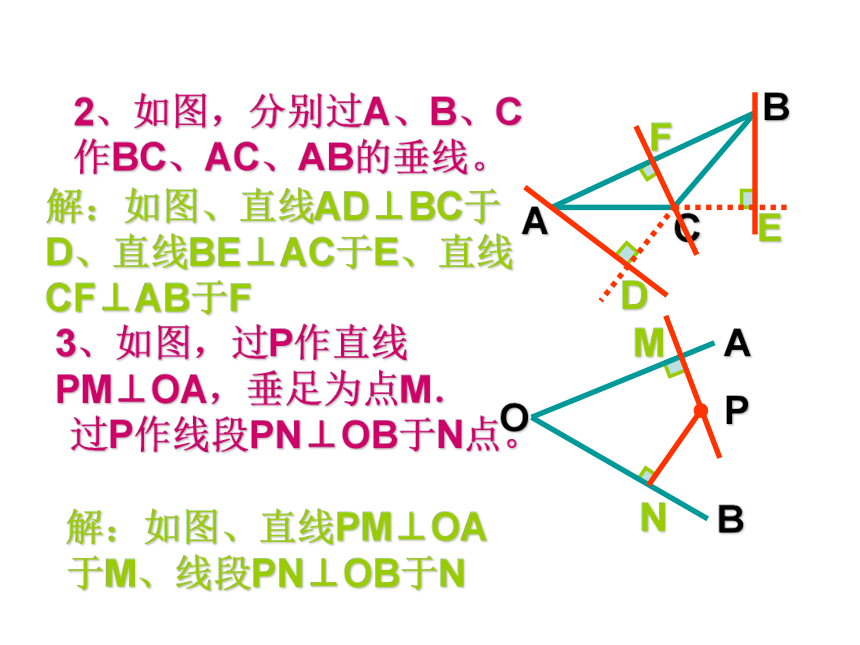
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条?存在性唯一性C线段、射线的垂线应怎么画呢? 练习:P7/练习EEE注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.2、如图,分别过A、B、C作BC、AC、AB的垂线。3、如图,过P作直线PM⊥OA,垂足为点M.
过P作线段PN⊥OB于N点。DEFMN解:如图、直线AD⊥BC于D、直线BE⊥AC于E、直线CF⊥AB于F解:如图、直线PM⊥OA于M、线段PN⊥OB于N思考 有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择什么样的路线尽快游到岸边m呢?连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。垂线段的长度简单说成:垂线段最短.1、已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条D选择题:B如图,怎样测量 点A 到 直线m 的距离?m1.过点A画出直线m的垂线AB,垂足为B;2.用直尺量出垂线段AB的长.AB 例1、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离。例2、如图, 1)画出线段BC的中点M,连结AM; 2)比较点B与点C到直线AM的距离。ABCPQ∴BP=CQ例3、如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长。MNMFABCDMN∴直线MF为所求垂线。??? 例4、如图2-23,试用直尺或三角板量出:
1.城市A与城市B的距离.
2.城市A,B到大河l的距离. 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。张庄拓展应用1垂线段最短拓 展 应 用2 如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。C∟垂线段最短立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离
小常识ABCDEFGM· · 问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。 问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么? 问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。┏
N你会设计吗? 在直角三角形的三条边中哪一条最长?思考答:直角所对的边即斜边最长.选择题:2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定DABCC想一想:DBCAE已知: 如图AD<AE <AC<AB 能说AD的长是A到BC的 距离吗?答:不能。?? 例2:如图2-22,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小解:∵ AC⊥BC于C,(已知)
∴ AC<AB.(垂线的性质二)
又∵ CD⊥AD于D,(已知)
∴ CD<AC.(垂线的性质二)
∵ DE⊥CE于E,(已知)
∴ DE<CD.(垂线的性质二)
∴ AB>AC>CD>DE.点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,试确定OE与OF的位置关系.并说明理由.延伸拓展解: OE⊥OF.理由如下: ∴ OE⊥OF.( )∵ OE平分∠AOC,(已知)又∵ OF平分∠BOC, 垂直的定义 角平分线的定义一个重要的基本图形回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗? 小结
怎么样画垂线?垂线的画法问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、O如图,已知直线 l,作l的垂线.工具:直尺、三角板A无数条1.垂线的画法:llA如图,已知直线l 和l上的一点A ,作 l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.请同学们画一下1.垂线的画法: 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条?存在性唯一性C线段、射线的垂线应怎么画呢? 练习:P7/练习EEE注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.2、如图,分别过A、B、C作BC、AC、AB的垂线。3、如图,过P作直线PM⊥OA,垂足为点M.
过P作线段PN⊥OB于N点。DEFMN解:如图、直线AD⊥BC于D、直线BE⊥AC于E、直线CF⊥AB于F解:如图、直线PM⊥OA于M、线段PN⊥OB于N思考 有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择什么样的路线尽快游到岸边m呢?连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。垂线段的长度简单说成:垂线段最短.1、已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条D选择题:B如图,怎样测量 点A 到 直线m 的距离?m1.过点A画出直线m的垂线AB,垂足为B;2.用直尺量出垂线段AB的长.AB 例1、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离。例2、如图, 1)画出线段BC的中点M,连结AM; 2)比较点B与点C到直线AM的距离。ABCPQ∴BP=CQ例3、如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长。MNMFABCDMN∴直线MF为所求垂线。??? 例4、如图2-23,试用直尺或三角板量出:
1.城市A与城市B的距离.
2.城市A,B到大河l的距离. 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。张庄拓展应用1垂线段最短拓 展 应 用2 如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。C∟垂线段最短立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离
小常识ABCDEFGM· · 问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。 问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么? 问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。┏
N你会设计吗? 在直角三角形的三条边中哪一条最长?思考答:直角所对的边即斜边最长.选择题:2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定DABCC想一想:DBCAE已知: 如图AD<AE <AC<AB 能说AD的长是A到BC的 距离吗?答:不能。?? 例2:如图2-22,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小解:∵ AC⊥BC于C,(已知)
∴ AC<AB.(垂线的性质二)
又∵ CD⊥AD于D,(已知)
∴ CD<AC.(垂线的性质二)
∵ DE⊥CE于E,(已知)
∴ DE<CD.(垂线的性质二)
∴ AB>AC>CD>DE.点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,试确定OE与OF的位置关系.并说明理由.延伸拓展解: OE⊥OF.理由如下: ∴ OE⊥OF.( )∵ OE平分∠AOC,(已知)又∵ OF平分∠BOC, 垂直的定义 角平分线的定义一个重要的基本图形回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗? 小结
