6.1平方根课件(第2课时)
文档属性
| 名称 | 6.1平方根课件(第2课时) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-31 08:25:01 | ||
图片预览





文档简介
(共22张PPT)
6.1 平方根
(第2课时)
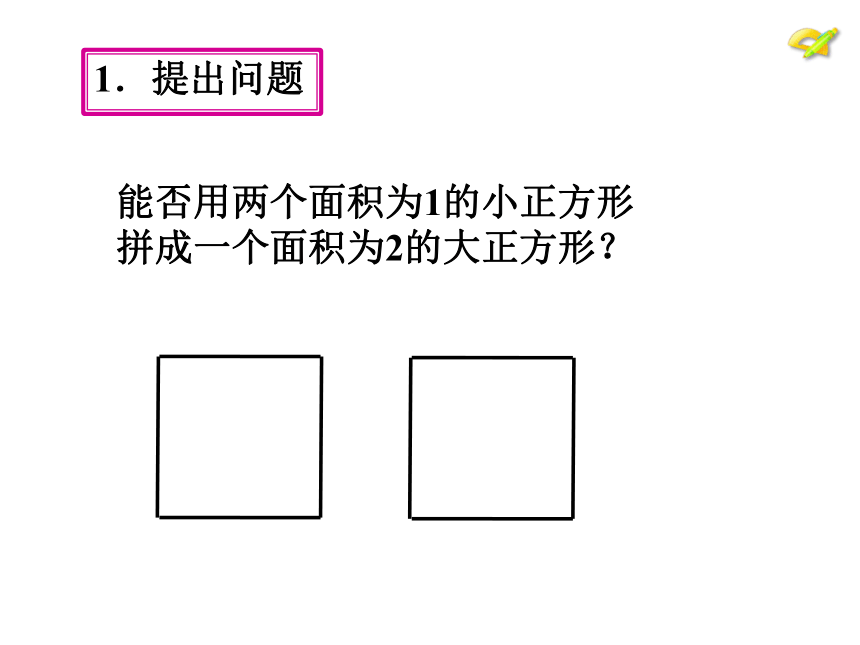
能否用两个面积为1的小正方形
拼成一个面积为2的大正方形?
1.提出问题
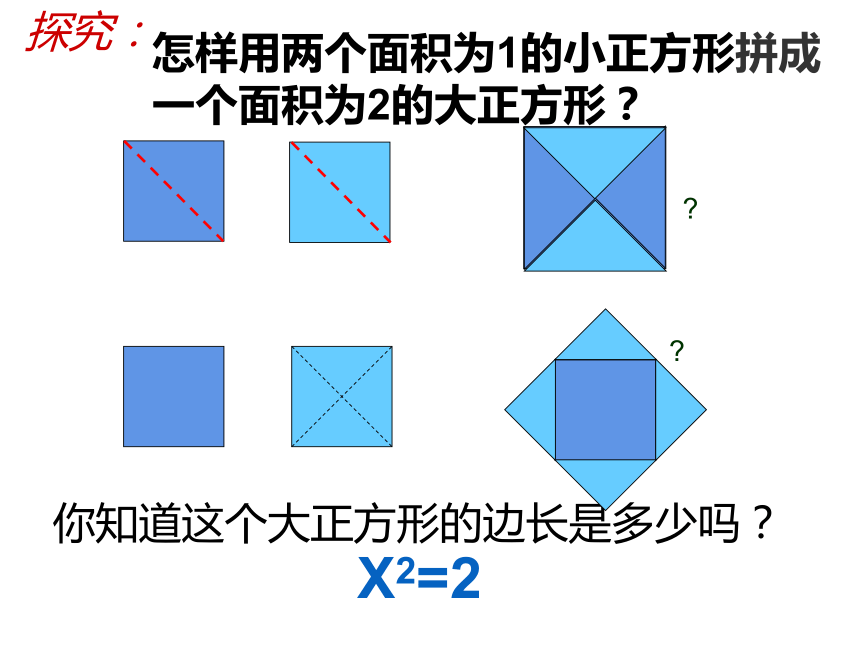
探究:
你知道这个大正方形的边长是多少吗?
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
X2=2
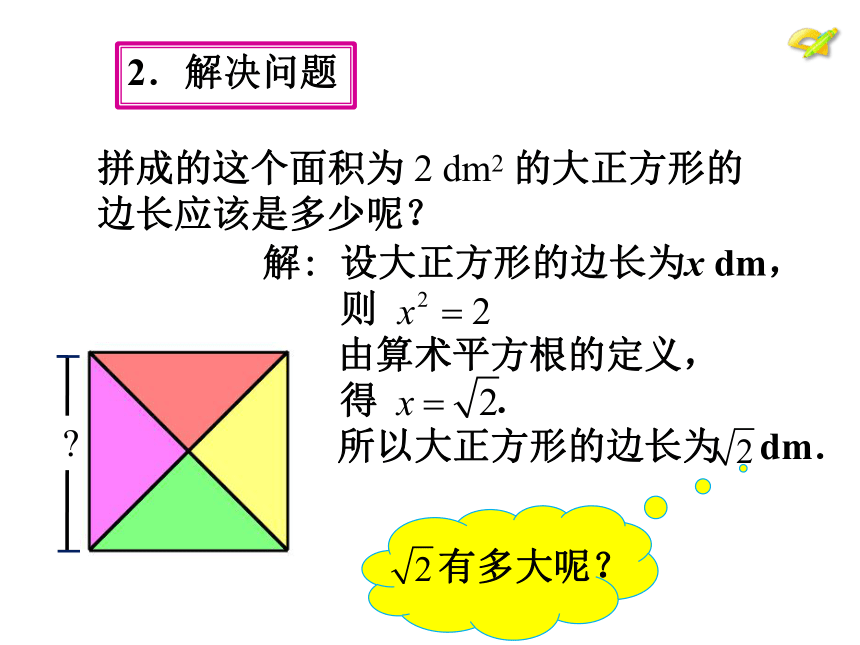
拼成的这个面积为 2 dm2 的大正方形的
边长应该是多少呢?
2.解决问题
解: 设大正方形的边长为x dm,
则
由算术平方根的定义,
得 .
所以大正方形的边长为 dm.
有多大呢?
有多大呢?
你是怎样判断出 大于1而小于2的?
你能不能得到 的更精确的范围?
2.解决问题
大于1而小于2
因为 , ,
而 < < ,
所以 .
有多大呢?
2.解决问题
因为 , ,而 ,
所以 .
因为 , ,
而 ,所以 .
因为 , ,
而 ,所以 .
……
有多大呢?
2.解决问题
你以前见过这种数吗?
“小数学家”妮妮就想到了一个办法:
①用 -1 来表示 的小数部分,你同意妮妮的表示方法吗?请说明理由.
②类似地, 的小数部分可以表示为_________;
的小数部分可以表示为_________;
③如果 的整数部分用m来表示,小数部分用n来表示,那么m、n分别是______,______.
-1
-2
感知估算、扩大认识
3
-3
是有限小数吗?
(它是一个小数位数无限,且小数部分不循环的小数.这样的数我们称之为无限不循环小数.)
你以前见过这种数吗?
它们是有理数吗?
π
例1 用计算器求下列各式的值: (1) ; (2) (精确到 ).
解:(1) 依次按键 3136
显示:56.
∴ .
2.用计算器求算术平方根
(2) 依次按键 2
显示:1.414213562.
∴ .
你会表示 吗?
3.解决章引言中提出的问题
你知道宇宙飞船离开地球进入轨道正常运行的
速度在什么范围吗?这时它的速度要大于第一
宇宙速度 (单位: )而小于第二宇宙速度 (单位: ). , 的大小满足 ,
,其中 ,R是地球半径, .怎样求 , 呢?
3.解决章引言中提出的问题
你会计算吗?
因此,第一宇宙速度 大约是 ,
第二宇宙 速度 大约是 .
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
… …
… 0.25 0.79 2.5 7.9 25 79 250 …
4.探究规律
被开方数每扩大100倍,
其算术平方根就扩大10倍
你发现其中有什么规律
被开方数越大,它的算术平方根越大.
被开方数的小数点每向右(或左)移动两位,
则它的算术平方根的小数点向右(或左)移动一位.
你能用计算器计算 (精确到0.001)吗?
并利用刚才的得到规律说出 ,
的近似值.
你能否根据 的值说出 是多少?
4.应用规律
例2 比较大小:
5.例题讲解
解:∵ 5>4,
∴ ,
∴ ,
∴ .
2、求 , 的整数与小数部分
练习:1、比较6与 的大小
35
小丽想用一块面积为400 cm2为的长方形纸片,沿着边的方向剪出一块面积为300 cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
5.例题讲解
你能将这个问题转化为数学问题吗?
解:设剪出的长方形的两边长分别为3x cm和2x cm,则有3x 2x=300 ,
6x2=300 ,
x2=50,
, 故长方形纸片的长为 ,宽为 .
5.例题讲解
长方形的长和宽与正方形的边长之间的大小关系是什么?小丽能用这块纸片裁出符合要求的纸片吗?
解:设剪出的长方形的两边长分别为3x cm和2x cm,则有3x 2x=300 ,
6x2=300 ,
x2=50,
, 故长方形纸片的长为 ,宽为 .
5.例题讲解
因为 50>49,得 >7 ,所以 >3×7=21,
比原正方形的边长更长,这是不可能的.所以,小丽不能用这块纸片裁出符合要求的纸片.
74500
11.18
0.3535
<
>
课堂检测
你发现其中有什么规律
被开方数越大,它的算术平方根越大.
被开方数的小数点每向右(或左)移动两位,
则它的算术平方根的小数点向右(或左)移动一位.
7.布置作业
教科书第44页练习 第1,2(1)、(2)、(4)题;习题6.1第6题
6.1 平方根
(第2课时)
能否用两个面积为1的小正方形
拼成一个面积为2的大正方形?
1.提出问题
探究:
你知道这个大正方形的边长是多少吗?
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
X2=2
拼成的这个面积为 2 dm2 的大正方形的
边长应该是多少呢?
2.解决问题
解: 设大正方形的边长为x dm,
则
由算术平方根的定义,
得 .
所以大正方形的边长为 dm.
有多大呢?
有多大呢?
你是怎样判断出 大于1而小于2的?
你能不能得到 的更精确的范围?
2.解决问题
大于1而小于2
因为 , ,
而 < < ,
所以 .
有多大呢?
2.解决问题
因为 , ,而 ,
所以 .
因为 , ,
而 ,所以 .
因为 , ,
而 ,所以 .
……
有多大呢?
2.解决问题
你以前见过这种数吗?
“小数学家”妮妮就想到了一个办法:
①用 -1 来表示 的小数部分,你同意妮妮的表示方法吗?请说明理由.
②类似地, 的小数部分可以表示为_________;
的小数部分可以表示为_________;
③如果 的整数部分用m来表示,小数部分用n来表示,那么m、n分别是______,______.
-1
-2
感知估算、扩大认识
3
-3
是有限小数吗?
(它是一个小数位数无限,且小数部分不循环的小数.这样的数我们称之为无限不循环小数.)
你以前见过这种数吗?
它们是有理数吗?
π
例1 用计算器求下列各式的值: (1) ; (2) (精确到 ).
解:(1) 依次按键 3136
显示:56.
∴ .
2.用计算器求算术平方根
(2) 依次按键 2
显示:1.414213562.
∴ .
你会表示 吗?
3.解决章引言中提出的问题
你知道宇宙飞船离开地球进入轨道正常运行的
速度在什么范围吗?这时它的速度要大于第一
宇宙速度 (单位: )而小于第二宇宙速度 (单位: ). , 的大小满足 ,
,其中 ,R是地球半径, .怎样求 , 呢?
3.解决章引言中提出的问题
你会计算吗?
因此,第一宇宙速度 大约是 ,
第二宇宙 速度 大约是 .
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
… …
… 0.25 0.79 2.5 7.9 25 79 250 …
4.探究规律
被开方数每扩大100倍,
其算术平方根就扩大10倍
你发现其中有什么规律
被开方数越大,它的算术平方根越大.
被开方数的小数点每向右(或左)移动两位,
则它的算术平方根的小数点向右(或左)移动一位.
你能用计算器计算 (精确到0.001)吗?
并利用刚才的得到规律说出 ,
的近似值.
你能否根据 的值说出 是多少?
4.应用规律
例2 比较大小:
5.例题讲解
解:∵ 5>4,
∴ ,
∴ ,
∴ .
2、求 , 的整数与小数部分
练习:1、比较6与 的大小
35
小丽想用一块面积为400 cm2为的长方形纸片,沿着边的方向剪出一块面积为300 cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
5.例题讲解
你能将这个问题转化为数学问题吗?
解:设剪出的长方形的两边长分别为3x cm和2x cm,则有3x 2x=300 ,
6x2=300 ,
x2=50,
, 故长方形纸片的长为 ,宽为 .
5.例题讲解
长方形的长和宽与正方形的边长之间的大小关系是什么?小丽能用这块纸片裁出符合要求的纸片吗?
解:设剪出的长方形的两边长分别为3x cm和2x cm,则有3x 2x=300 ,
6x2=300 ,
x2=50,
, 故长方形纸片的长为 ,宽为 .
5.例题讲解
因为 50>49,得 >7 ,所以 >3×7=21,
比原正方形的边长更长,这是不可能的.所以,小丽不能用这块纸片裁出符合要求的纸片.
74500
11.18
0.3535
<
>
课堂检测
你发现其中有什么规律
被开方数越大,它的算术平方根越大.
被开方数的小数点每向右(或左)移动两位,
则它的算术平方根的小数点向右(或左)移动一位.
7.布置作业
教科书第44页练习 第1,2(1)、(2)、(4)题;习题6.1第6题
