福建省厦门市第六中学2023-2024学年高二上学期期中考试数学试题(扫描版含答案)
文档属性
| 名称 | 福建省厦门市第六中学2023-2024学年高二上学期期中考试数学试题(扫描版含答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 09:49:27 | ||
图片预览



文档简介
厦门六中2023一2024学年第一学期高二年期中考试
数学试卷
满分150分考试时间120分钟
一、单项选择题:本大题共8小题,只有一项符合题目要求,每小题5分,共
40分)
1.两条平行直线1:3x+4y-5=0与12:6x+8y-5=0之间的距离是
A.0
B.2、
C.1
D.2
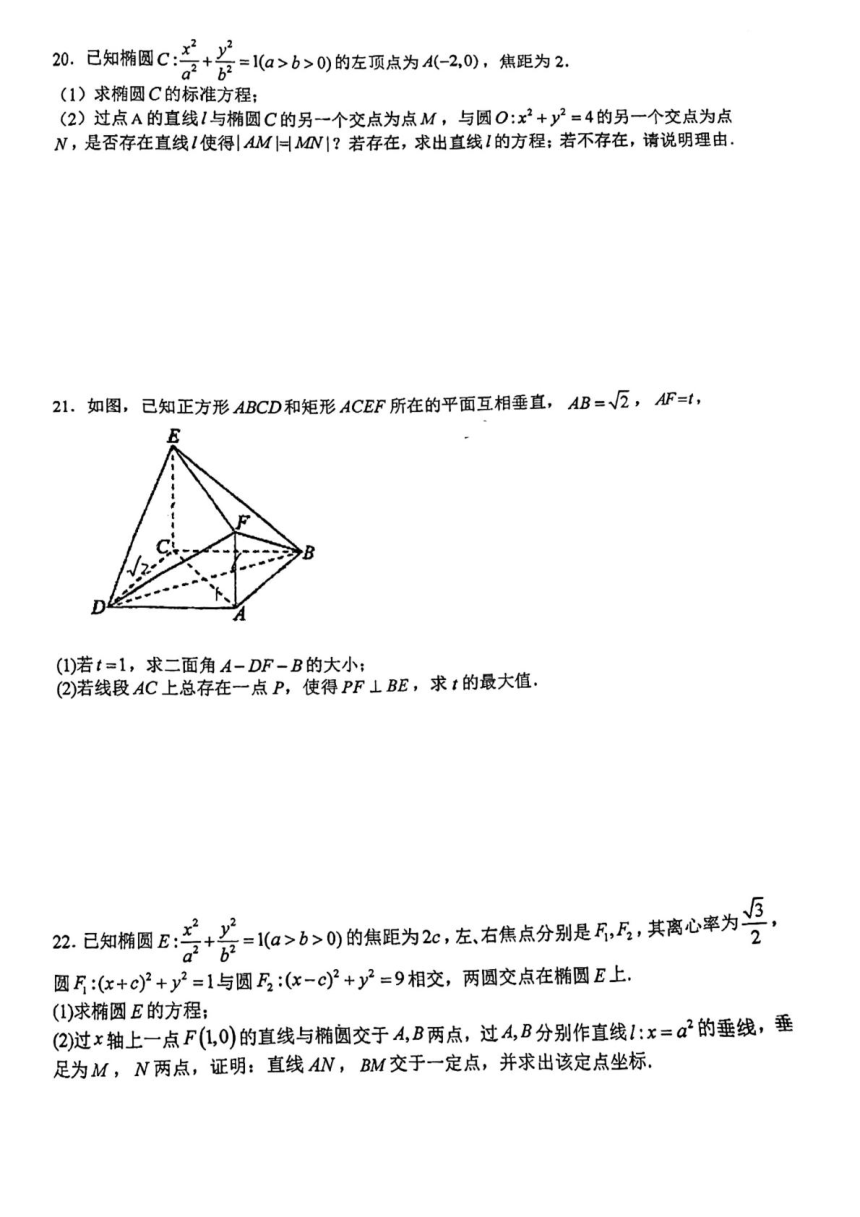
2.焦点在y轴上,且长轴长与短轴长之比为2:1,焦距为2√5的椭圆方程为
A号+y2=1
B.号+y=1
c.x2+上=1
2
D+片=l
3.从M(0,2,1)出发的光线,经平面xOy反射后到达点N(2,0,2),则光线所行走的路
程为
A.3
B.4
C.7
D.35
4.已知椭圆兰+上
=1上一点M到左焦点F的距离为6,N是M的中点,则ON=
1612
A..1
.2
C.3
)D.4
5.己知O为空间任意一点,A、B、C、P满足任意三点不共线,但四点共面,且
BP=mOA+OB+OC,则m的值为
A.-1
B.2
C.-2
D.-3
6.在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹
方程,下表给出了一些条件及方程:
条件
方程
①△ABC周长为10
Cy2-25
②△ABC面积为10
C2:x2+y2=4y≠0)
③△ABC中,∠A=90°
6号+=00
则满足条件①、②、③的点A轨迹方程按顺序分别是
A.C2、C、CB.C3、C、C2
C.C、C、C2
D.C、C2、C
7.已知点A(-2,0),点B(4,0),点P在圆(x-3)2+y-4)2=20上,则使得PA⊥PB的点P
的个数为
A.0
B.1
C.2
D.3
8.已知椭圆C:x,±=1(a>b>0),点,F2是椭圆的左、右焦点,点A是椭圆上一点,
△AE的内切圆的圆心为M,若3M+2M瓦+MA=0,则椭圆的离心率为
A.
D.1
5
B.月
c
二.多项选择题(本大题共4小题,每题全部选对得5分,选对但不全的得2
分,有错选的得0分,共20分)
9.仁知直线1的倾斜角为120°,且直线1经过点(-1,2),则下列结论中正确的是
A.直线1的一个方向向量为ā=(L,V5)B.直线l与直线x-y=0垂直
C.直线l在x轴上的截距等于2
D.点(-1,O)到直线1上的点的最短距离是1
3
10.在空间直角坐标系0-z中,0是坐标原点,A(0,1,0),B(-1,2,1),C(1,3,-1),下列
选项中,正确的有
A.AB⊥BC
‘B.平面ABC的一个法向量是(1,O,)
C,AMBC的面积是3V2
2
D.点0到直线AB的距离是
3
11.已知椭圆C:
二+上-1,万,R分别为它的左右焦点,若点P是椭圆上异于长轴端点
259
的一个动点,M(1,),下列结论中正确的有
A,△PF的周长为15
3过椭圆C上一点4,的切线方程为4x+5y-25
C.|PM+P的最大值为12
D.若M是直线1与椭圆C相交弦AB的中点,则1方程为:9x+25y-34=0
12.已知圆C:(x-1)2+((y-2)2=2,点M是直线1:y=-x-1上的动点,过点M作圆C的两
条切线,切点分别为A、B,则下列说法正确的是
A.四边形ACBM面积的最小值为2√5
B.∠ACB的最小值为120°
C.若P2是圆C的一条直径,则MP.M⑨的最小值为7
13
D.直线AB恒过定点
22
三.填空题:本题共4小题,每小题5分,共20分.
13.
已知方程xy
=1表示焦点在x轴上的椭圆,则实数k的取值范围为
k+53-k
14.己知点M在桶圆多+兰=1上运动!点W在圆x-3}+y=1上运动,则MW的最大值
189
为
15.已知经过点P(oyo,)且法向量为E=(A,B,C)的平面的方程是A(x-)+B(y
-%)+C(z-z)=0”.现知道平面α的方程为×+2z号1,则过M(1,2,3)与N(3,2,4)的直
线与平面α所成角的余弦值是
16.古希腊数学家阿波罗尼奥斯发现:平面上到两定点A,B距离之比2(2>0,2≠1)是常数
的点的轨迹是一个圆心在直线AB上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的
问题:在棱长为1的正方体ABCD-ABCD,中,点P是正方体的表面ADD,A(包括边界)
上的动点,若动点P满足PA=2PD,则点P所形成的阿氏圆的半径为一:三楼锥
P-ACD体积的最大值是
数学试卷
满分150分考试时间120分钟
一、单项选择题:本大题共8小题,只有一项符合题目要求,每小题5分,共
40分)
1.两条平行直线1:3x+4y-5=0与12:6x+8y-5=0之间的距离是
A.0
B.2、
C.1
D.2
2.焦点在y轴上,且长轴长与短轴长之比为2:1,焦距为2√5的椭圆方程为
A号+y2=1
B.号+y=1
c.x2+上=1
2
D+片=l
3.从M(0,2,1)出发的光线,经平面xOy反射后到达点N(2,0,2),则光线所行走的路
程为
A.3
B.4
C.7
D.35
4.已知椭圆兰+上
=1上一点M到左焦点F的距离为6,N是M的中点,则ON=
1612
A..1
.2
C.3
)D.4
5.己知O为空间任意一点,A、B、C、P满足任意三点不共线,但四点共面,且
BP=mOA+OB+OC,则m的值为
A.-1
B.2
C.-2
D.-3
6.在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹
方程,下表给出了一些条件及方程:
条件
方程
①△ABC周长为10
Cy2-25
②△ABC面积为10
C2:x2+y2=4y≠0)
③△ABC中,∠A=90°
6号+=00
则满足条件①、②、③的点A轨迹方程按顺序分别是
A.C2、C、CB.C3、C、C2
C.C、C、C2
D.C、C2、C
7.已知点A(-2,0),点B(4,0),点P在圆(x-3)2+y-4)2=20上,则使得PA⊥PB的点P
的个数为
A.0
B.1
C.2
D.3
8.已知椭圆C:x,±=1(a>b>0),点,F2是椭圆的左、右焦点,点A是椭圆上一点,
△AE的内切圆的圆心为M,若3M+2M瓦+MA=0,则椭圆的离心率为
A.
D.1
5
B.月
c
二.多项选择题(本大题共4小题,每题全部选对得5分,选对但不全的得2
分,有错选的得0分,共20分)
9.仁知直线1的倾斜角为120°,且直线1经过点(-1,2),则下列结论中正确的是
A.直线1的一个方向向量为ā=(L,V5)B.直线l与直线x-y=0垂直
C.直线l在x轴上的截距等于2
D.点(-1,O)到直线1上的点的最短距离是1
3
10.在空间直角坐标系0-z中,0是坐标原点,A(0,1,0),B(-1,2,1),C(1,3,-1),下列
选项中,正确的有
A.AB⊥BC
‘B.平面ABC的一个法向量是(1,O,)
C,AMBC的面积是3V2
2
D.点0到直线AB的距离是
3
11.已知椭圆C:
二+上-1,万,R分别为它的左右焦点,若点P是椭圆上异于长轴端点
259
的一个动点,M(1,),下列结论中正确的有
A,△PF的周长为15
3过椭圆C上一点4,的切线方程为4x+5y-25
C.|PM+P的最大值为12
D.若M是直线1与椭圆C相交弦AB的中点,则1方程为:9x+25y-34=0
12.已知圆C:(x-1)2+((y-2)2=2,点M是直线1:y=-x-1上的动点,过点M作圆C的两
条切线,切点分别为A、B,则下列说法正确的是
A.四边形ACBM面积的最小值为2√5
B.∠ACB的最小值为120°
C.若P2是圆C的一条直径,则MP.M⑨的最小值为7
13
D.直线AB恒过定点
22
三.填空题:本题共4小题,每小题5分,共20分.
13.
已知方程xy
=1表示焦点在x轴上的椭圆,则实数k的取值范围为
k+53-k
14.己知点M在桶圆多+兰=1上运动!点W在圆x-3}+y=1上运动,则MW的最大值
189
为
15.已知经过点P(oyo,)且法向量为E=(A,B,C)的平面的方程是A(x-)+B(y
-%)+C(z-z)=0”.现知道平面α的方程为×+2z号1,则过M(1,2,3)与N(3,2,4)的直
线与平面α所成角的余弦值是
16.古希腊数学家阿波罗尼奥斯发现:平面上到两定点A,B距离之比2(2>0,2≠1)是常数
的点的轨迹是一个圆心在直线AB上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的
问题:在棱长为1的正方体ABCD-ABCD,中,点P是正方体的表面ADD,A(包括边界)
上的动点,若动点P满足PA=2PD,则点P所形成的阿氏圆的半径为一:三楼锥
P-ACD体积的最大值是
同课章节目录
