新人教版八年数学下18.2.3正方形课件
文档属性
| 名称 | 新人教版八年数学下18.2.3正方形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-31 00:00:00 | ||
图片预览







文档简介
课件20张PPT。东丰四中 郑晓平§18.2 .3 正方形学习目标:
1.掌握正方形的概念、性质和判定并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别;
学习重点:
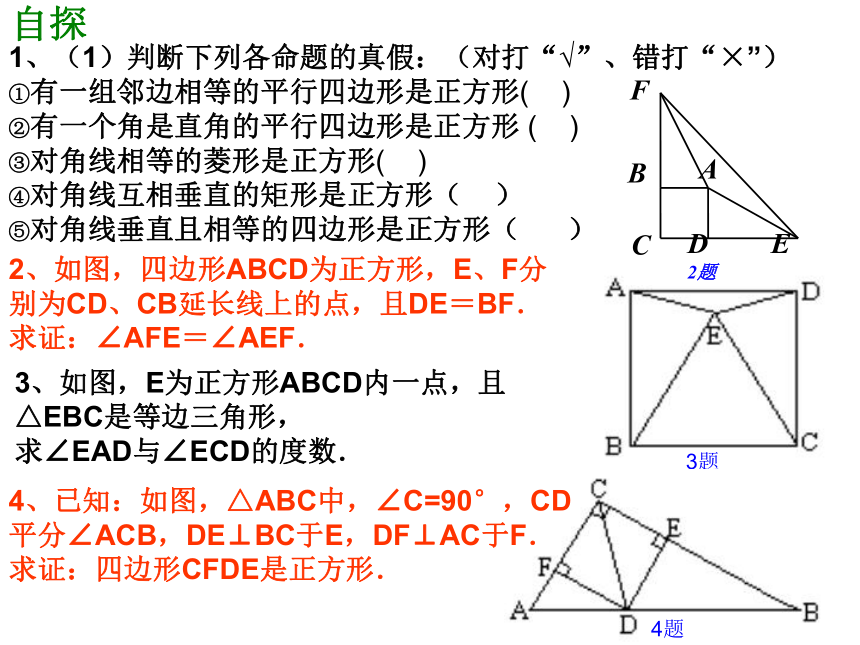
正方形的性质和判定1、(1)判断下列各命题的真假:(对打“√”、错打“×”)
①有一组邻边相等的平行四边形是正方形( )
②有一个角是直角的平行四边形是正方形 ( )
③对角线相等的菱形是正方形( )
④对角线互相垂直的矩形是正方形( )
⑤对角线垂直且相等的四边形是正方形( )
3、如图,E为正方形ABCD内一点,且△EBC是等边三角形,
求∠EAD与∠ECD的度数.2、如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF.
求证:∠AFE=∠AEF.
自探4、已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.自探提示------疑而探之则明
1、请同学们对独立完成的1~4题明确思路。
2、实在有困惑之处,可以在有问题的位置做好标注,留待合探时在小组内交流解决。
(整理时间2分钟)解疑合探------独学而无友则孤陋而寡闻合探要求
1、小组讨论,交流自探成果。
2、小组长带领,人人参与,有序进行重点解决自探中的疑难问题达成共识。
3、小组长作好记录,以备展示和点评。
(5分钟)1、展示要求:
书写迅速,字迹工整,内容简练,思路清晰,格式规范。2、评价要求:
点评声音洪亮,条理清晰,突出重点,语言简练。
恰当的指出展示成果的优点和缺点,并打分。解疑合探1、已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.2、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:EA⊥AF.运用拓展变式一、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.若AD=4,DE=2
求:EF的长.运用拓展变式二、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF .若AE=20,正方形ABCD的面积为256.
求:BF的长.运用拓展3、请同学们结合本节内容自编一道小题考考你的同学。感悟与收获作业1、(作业小本)教科书62页第13题
2、测评 第38页(五)(六)
再见回顾思考 提出问题 如图,某一拉门在完全关闭时,其相应的菱形变成
正方形.请说说图中∠1的变化过程.回顾思考 提出问题 现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形. 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 平行四边形矩形菱形正
方
形平行四边形、矩形、菱形、正方形的关系
1.掌握正方形的概念、性质和判定并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别;
学习重点:
正方形的性质和判定1、(1)判断下列各命题的真假:(对打“√”、错打“×”)
①有一组邻边相等的平行四边形是正方形( )
②有一个角是直角的平行四边形是正方形 ( )
③对角线相等的菱形是正方形( )
④对角线互相垂直的矩形是正方形( )
⑤对角线垂直且相等的四边形是正方形( )
3、如图,E为正方形ABCD内一点,且△EBC是等边三角形,
求∠EAD与∠ECD的度数.2、如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF.
求证:∠AFE=∠AEF.
自探4、已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.自探提示------疑而探之则明
1、请同学们对独立完成的1~4题明确思路。
2、实在有困惑之处,可以在有问题的位置做好标注,留待合探时在小组内交流解决。
(整理时间2分钟)解疑合探------独学而无友则孤陋而寡闻合探要求
1、小组讨论,交流自探成果。
2、小组长带领,人人参与,有序进行重点解决自探中的疑难问题达成共识。
3、小组长作好记录,以备展示和点评。
(5分钟)1、展示要求:
书写迅速,字迹工整,内容简练,思路清晰,格式规范。2、评价要求:
点评声音洪亮,条理清晰,突出重点,语言简练。
恰当的指出展示成果的优点和缺点,并打分。解疑合探1、已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.2、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:EA⊥AF.运用拓展变式一、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.若AD=4,DE=2
求:EF的长.运用拓展变式二、已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF .若AE=20,正方形ABCD的面积为256.
求:BF的长.运用拓展3、请同学们结合本节内容自编一道小题考考你的同学。感悟与收获作业1、(作业小本)教科书62页第13题
2、测评 第38页(五)(六)
再见回顾思考 提出问题 如图,某一拉门在完全关闭时,其相应的菱形变成
正方形.请说说图中∠1的变化过程.回顾思考 提出问题 现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形. 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 平行四边形矩形菱形正
方
形平行四边形、矩形、菱形、正方形的关系
