2024人教A版数学必修第一册(课时检测双练)2.1.1不等关系与不等式(含解析)
文档属性
| 名称 | 2024人教A版数学必修第一册(课时检测双练)2.1.1不等关系与不等式(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 65.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 10:13:18 | ||
图片预览

文档简介
2.1.1不等关系与不等式
一、选择题
1.大桥头竖立的“限重40吨”的警示牌,是提示司机要安全通过该桥,应使车货总重量T不超过40吨,用不等式表示为( )
A.T<40 B.T>40 C.T≤40 D.T≥40
2.设a=3x2-x+1,b=2x2+x,x∈R,则( )
A.a>b B.a<b
C.a≥b D.a≤b
3.若a≠2且b≠-1,则M=a2+b2-4a+2b的值与-5的大小关系是( )
A.M>-5 B.M<-5
C.M=-5 D.不能确定
4.b克糖水中有a克糖(b>a>0),若再添上m克糖(m>0),则糖水变甜了,根据这个事实提炼的一个不等式为( )
A.< B.>
C.< D.>
5.已知c>1,且x=,y=,则x,y之间的大小关系是( )
A.x>y
B.x=y
C.x<y
D.x,y的关系随c而定
二、填空题
6.若x∈R,则与的大小关系为________.
7.一辆汽车原来每天行驶x km,如果该汽车每天行驶的路程比原来多19 km,那么在8天内它的行程将超过2 200 km,用不等式表示为________.
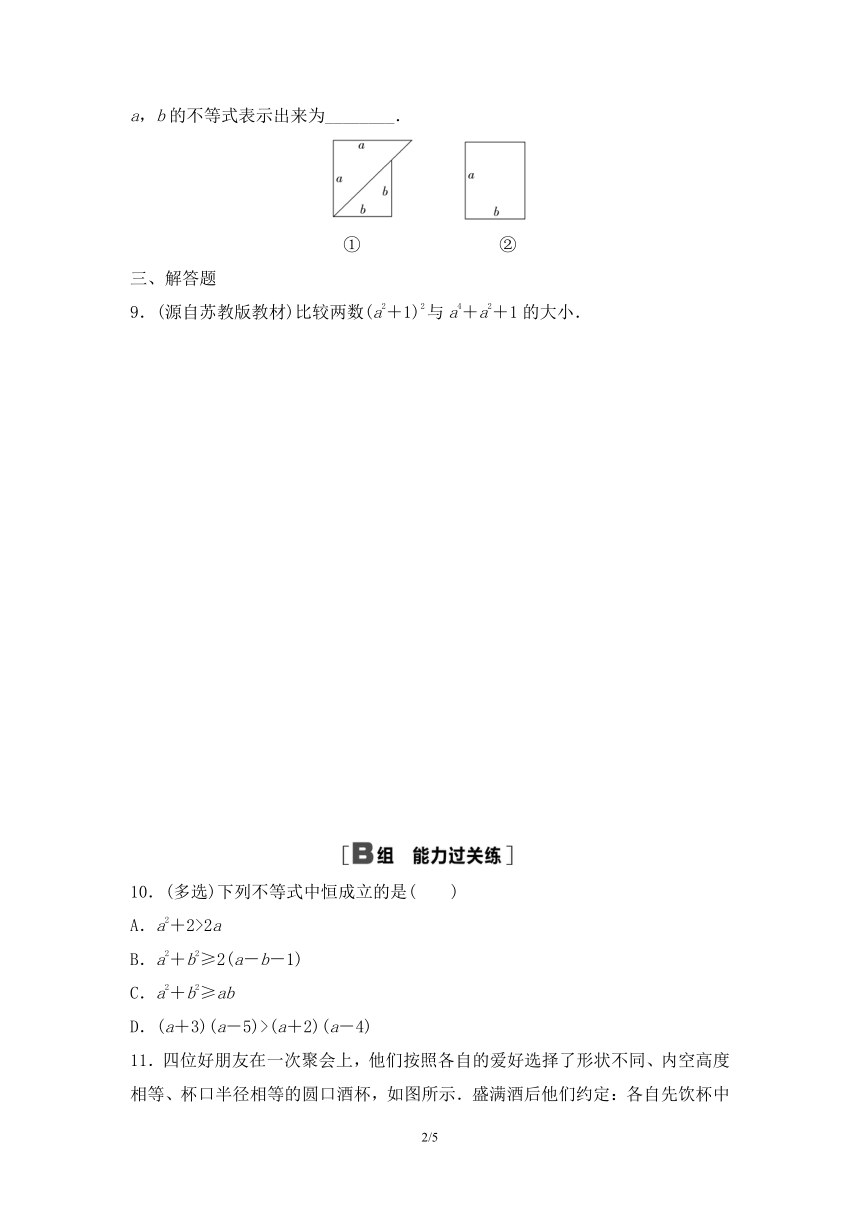
8.如图所示的两种广告牌,其中图①是由两个等腰直角三角形构成的,图②是一个矩形,从图形上确定这两个广告牌面积的大小关系,并将这种关系用含字母a,b的不等式表示出来为________.
① ②
三、解答题
9.(源自苏教版教材)比较两数(a2+1)2与a4+a2+1的大小.
10.(多选)下列不等式中恒成立的是( )
A.a2+2>2a
B.a2+b2≥2(a-b-1)
C.a2+b2≥ab
D.(a+3)(a-5)>(a+2)(a-4)
11.四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示.盛满酒后他们约定:各自先饮杯中酒的一半.设剩余酒的高度从左到右依次为h1,h2,h3,h4,则它们的大小关系正确的是( )
A.h2>h1>h4 B.h1>h2>h3
C.h3>h2>h4 D.h2>h4>h1
12.一个棱长为2的正方体的上底面有一点A,下底面有一点B,则A,B两点间的距离d满足的不等式为________.
13.已知a,b∈R,若ab=1,则a2+b2的最小值是________,当且仅当a=b=______时取得最小值.
14.(2022·广东深圳实验学校高中部月考)(1)已知a1,a2,b1,b2是实数,求证:
()≥(a1 b1 + a2 b2 )2;
(2)已知a>0,b>0,c>0,且a+b+c=2,求证:a2+b2+c2≥.
15.建筑设计规定,民用住宅的窗户面积必须小于地板面积.但按采光标准,窗户面积与地板面积的比值应不小于10%,且这个比值越大,住宅的采光条件就越好,试问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
1.C [限重就是不超过,可以直接建立不等式T≤40.故选C.]
2.C [∵a-b=x2-2x+1=(x-1)2≥0,
∴a≥b.故选C.]
3.A [M=(a-2)2+(b+1)2-5>-5.故选A.]
4.B [糖水变甜了,说明糖水中糖的浓度增加了,故a+m,b+m>a,b.故选B.]
5.C [用作商法比较,由题意x,y>0,
∵=,=<1,且y>0∴x<y.故选C.]
6.≤ [∵-==≤0,∴≤.]
7.8(x+19)>2 200 [因为该汽车每天行驶的路程比原来多19 km,所以汽车现在每天行驶的路程为(x+19)km,则在8天内它的行程为8(x+19)km,因此,不等关系“在8天内它的行程将超过2 200 km”可以用不等式8(x+19)>2 200来表示.]
8.(a2+b2)>ab [由题图可知,题图①广告牌的面积S1= (a2+b2),题图②广告牌的面积S2=ab,观察题图得S1>S2,即 (a2+b2)>ab.]
9.解:因为(a2+1)2-(a4+a2+1)
=a4+2a2+1-a4-a2-1
=a2.
当a=0时,a2=0,所以(a2+1)2=a4+a2+1;
当a≠0时,a2>0,所以(a2+1)2>a4+a2+1.
10.ABC [A中,a2+2-2a=(a-1)2+1>0,故A正确;B中,a2+b2-2(a-b-1)=a2-2a+b2+2b+2=(a-1)2+(b+1)2≥0,故B正确;C中,a2+b2-ab=a2-ab+b2+b2=+b2≥0,故C正确;D中,因为(a+3)(a-5)-(a+2)·(a-4)=-7<0,所以(a+3)(a-5)<(a+2)(a-4),故D错误.]
11.A [由题图可知体积缩小一半后剩余酒的高度最高为h2,最低为h4,故选A.]
12.2≤d≤23 [最短距离是棱长2,最长距离是正方体的体对角线长23.故2≤d≤23.]
13.2 ±1 [根据a2+b2-2ab=(a-b)2≥0,故a2+b2≥2ab=2,当且仅当a-b=0即a=b=±1时等号成立.]
14.证明:(1)(a21+a22)(b21+b22)-(a1b1+a2b2)2
=a21b21+a21b22+a22b21+a22b22-a21b21-2a1b1a2b2-a22b22
=a21b22+a22b21-2a1b1a2b2=(a1b2-a2b1)2≥0,
当且仅当a1b2-a2b1=0时,取等号,
∴对任意实数a1,a2,b1,b2,
(a21+a22)(b21+b22)≥(a1b1+a2b2)2成立.
(2)∵a+b+c=2,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=4.
∵a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
≤a2+b2+c2+a2+b2+a2+c2+b2+c2
=3(a2+b2+c2),
∴3(a2+b2+c2)≥(a+b+c)2=4,
∴a2+b2+c2≥.
15.解:设住宅窗户面积、地板面积分别为a,b,同时增加的面积为m,根据问题的要求a0,于是>.又≥10%,因此>≥10%.所以同时增加相等的窗户面积和地板面积后,住宅的采光条件变好了.
1/5
一、选择题
1.大桥头竖立的“限重40吨”的警示牌,是提示司机要安全通过该桥,应使车货总重量T不超过40吨,用不等式表示为( )
A.T<40 B.T>40 C.T≤40 D.T≥40
2.设a=3x2-x+1,b=2x2+x,x∈R,则( )
A.a>b B.a<b
C.a≥b D.a≤b
3.若a≠2且b≠-1,则M=a2+b2-4a+2b的值与-5的大小关系是( )
A.M>-5 B.M<-5
C.M=-5 D.不能确定
4.b克糖水中有a克糖(b>a>0),若再添上m克糖(m>0),则糖水变甜了,根据这个事实提炼的一个不等式为( )
A.< B.>
C.< D.>
5.已知c>1,且x=,y=,则x,y之间的大小关系是( )
A.x>y
B.x=y
C.x<y
D.x,y的关系随c而定
二、填空题
6.若x∈R,则与的大小关系为________.
7.一辆汽车原来每天行驶x km,如果该汽车每天行驶的路程比原来多19 km,那么在8天内它的行程将超过2 200 km,用不等式表示为________.
8.如图所示的两种广告牌,其中图①是由两个等腰直角三角形构成的,图②是一个矩形,从图形上确定这两个广告牌面积的大小关系,并将这种关系用含字母a,b的不等式表示出来为________.
① ②
三、解答题
9.(源自苏教版教材)比较两数(a2+1)2与a4+a2+1的大小.
10.(多选)下列不等式中恒成立的是( )
A.a2+2>2a
B.a2+b2≥2(a-b-1)
C.a2+b2≥ab
D.(a+3)(a-5)>(a+2)(a-4)
11.四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示.盛满酒后他们约定:各自先饮杯中酒的一半.设剩余酒的高度从左到右依次为h1,h2,h3,h4,则它们的大小关系正确的是( )
A.h2>h1>h4 B.h1>h2>h3
C.h3>h2>h4 D.h2>h4>h1
12.一个棱长为2的正方体的上底面有一点A,下底面有一点B,则A,B两点间的距离d满足的不等式为________.
13.已知a,b∈R,若ab=1,则a2+b2的最小值是________,当且仅当a=b=______时取得最小值.
14.(2022·广东深圳实验学校高中部月考)(1)已知a1,a2,b1,b2是实数,求证:
()≥(a1 b1 + a2 b2 )2;
(2)已知a>0,b>0,c>0,且a+b+c=2,求证:a2+b2+c2≥.
15.建筑设计规定,民用住宅的窗户面积必须小于地板面积.但按采光标准,窗户面积与地板面积的比值应不小于10%,且这个比值越大,住宅的采光条件就越好,试问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
1.C [限重就是不超过,可以直接建立不等式T≤40.故选C.]
2.C [∵a-b=x2-2x+1=(x-1)2≥0,
∴a≥b.故选C.]
3.A [M=(a-2)2+(b+1)2-5>-5.故选A.]
4.B [糖水变甜了,说明糖水中糖的浓度增加了,故a+m,b+m>a,b.故选B.]
5.C [用作商法比较,由题意x,y>0,
∵=,=<1,且y>0∴x<y.故选C.]
6.≤ [∵-==≤0,∴≤.]
7.8(x+19)>2 200 [因为该汽车每天行驶的路程比原来多19 km,所以汽车现在每天行驶的路程为(x+19)km,则在8天内它的行程为8(x+19)km,因此,不等关系“在8天内它的行程将超过2 200 km”可以用不等式8(x+19)>2 200来表示.]
8.(a2+b2)>ab [由题图可知,题图①广告牌的面积S1= (a2+b2),题图②广告牌的面积S2=ab,观察题图得S1>S2,即 (a2+b2)>ab.]
9.解:因为(a2+1)2-(a4+a2+1)
=a4+2a2+1-a4-a2-1
=a2.
当a=0时,a2=0,所以(a2+1)2=a4+a2+1;
当a≠0时,a2>0,所以(a2+1)2>a4+a2+1.
10.ABC [A中,a2+2-2a=(a-1)2+1>0,故A正确;B中,a2+b2-2(a-b-1)=a2-2a+b2+2b+2=(a-1)2+(b+1)2≥0,故B正确;C中,a2+b2-ab=a2-ab+b2+b2=+b2≥0,故C正确;D中,因为(a+3)(a-5)-(a+2)·(a-4)=-7<0,所以(a+3)(a-5)<(a+2)(a-4),故D错误.]
11.A [由题图可知体积缩小一半后剩余酒的高度最高为h2,最低为h4,故选A.]
12.2≤d≤23 [最短距离是棱长2,最长距离是正方体的体对角线长23.故2≤d≤23.]
13.2 ±1 [根据a2+b2-2ab=(a-b)2≥0,故a2+b2≥2ab=2,当且仅当a-b=0即a=b=±1时等号成立.]
14.证明:(1)(a21+a22)(b21+b22)-(a1b1+a2b2)2
=a21b21+a21b22+a22b21+a22b22-a21b21-2a1b1a2b2-a22b22
=a21b22+a22b21-2a1b1a2b2=(a1b2-a2b1)2≥0,
当且仅当a1b2-a2b1=0时,取等号,
∴对任意实数a1,a2,b1,b2,
(a21+a22)(b21+b22)≥(a1b1+a2b2)2成立.
(2)∵a+b+c=2,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=4.
∵a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
≤a2+b2+c2+a2+b2+a2+c2+b2+c2
=3(a2+b2+c2),
∴3(a2+b2+c2)≥(a+b+c)2=4,
∴a2+b2+c2≥.
15.解:设住宅窗户面积、地板面积分别为a,b,同时增加的面积为m,根据问题的要求a
1/5
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
