第四章 几何图形初步单元练习(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第四章 几何图形初步 单元练习 2022-2023学年人教版数学七年级上册
一、单选题
1.一个角是这个角的余角的2倍,则这个角的度数是( )
A.30° B.45° C.60° D.75°
2.已知点A,B,C在同一直线上, , ,则线段AC的长是( )
A.8cm B.2cm C.8cm或2cm D.不能确定
3.下列说法错误的是( )
A.若AC=BC,则C是线段AB的中点
B.平面内过一点有且只有一条直线与已知直线垂直
C.平行于同一直线的两条直线平行
D.一副七巧板中只有一个平行四边形,且面积大小占这副七巧板面积总和的
4.如图,下列各式中错误的是( )
A.AB=AD+DB B.CB=AB﹣AC C.CD=CB﹣DB D.AC=CB﹣DB
5.如图,已知 ,点 是 的中点,点 又是 的中点,则 ( ).
A. B. C. D.
6.如图所示,点O为直线AB上一点∠AOC=∠DOE=90°,那么图中互余角的对数为( )
A.2对 B.3对 C.4对 D.5对
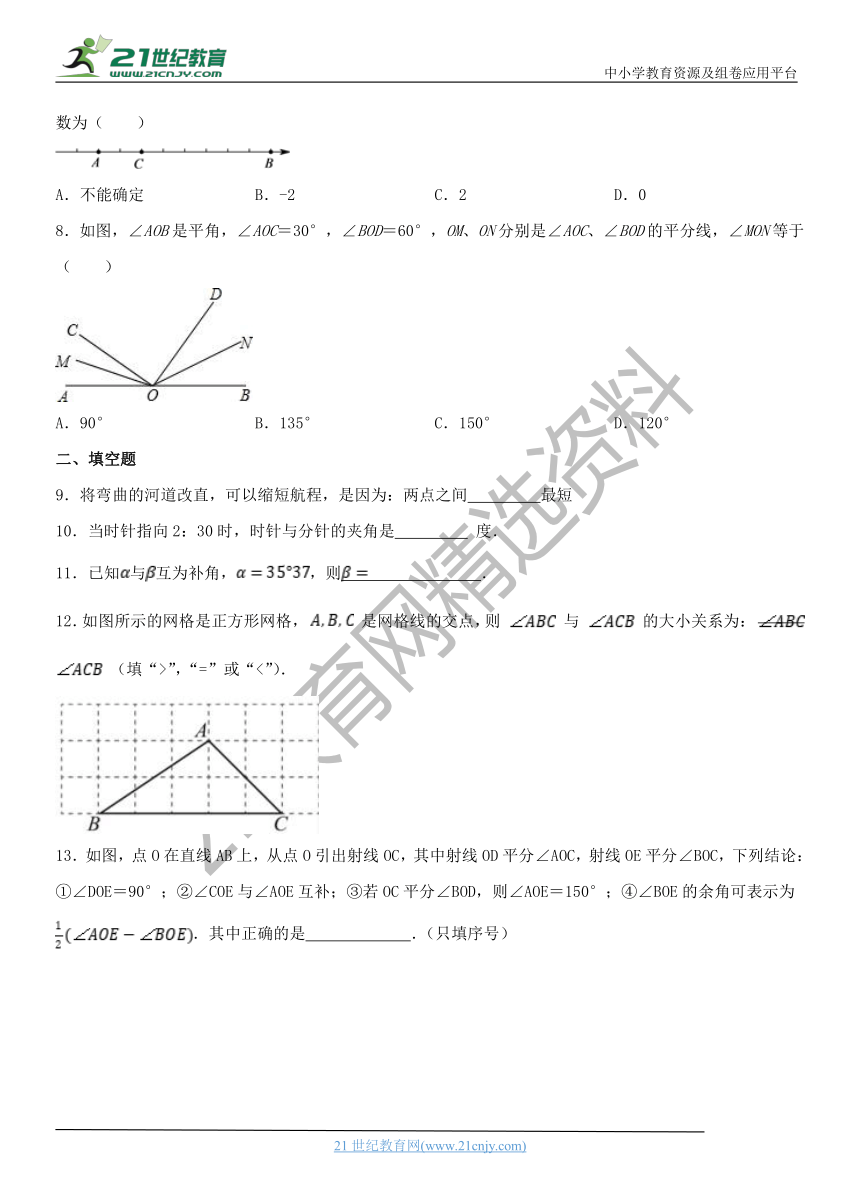
7.如图,数轴上有三个点A、B、C,且A、B表示的数互为相反数,若每个单位长度表示1,则点C表示的数为( )
A.不能确定 B.-2 C.2 D.0
8.如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,∠MON等于( )
A.90° B.135° C.150° D.120°
二、填空题
9.将弯曲的河道改直,可以缩短航程,是因为:两点之间 最短
10.当时针指向2:30时,时针与分针的夹角是 度.
11.已知与互为补角,,则 .
12.如图所示的网格是正方形网格, 是网格线的交点,则 与 的大小关系为: (填“>”,“=”或“<”).
13.如图,点O在直线AB上,从点O引出射线OC,其中射线OD平分∠AOC,射线OE平分∠BOC,下列结论:①∠DOE=90°;②∠COE与∠AOE互补;③若OC平分∠BOD,则∠AOE=150°;④∠BOE的余角可表示为.其中正确的是 .(只填序号)
三、解答题
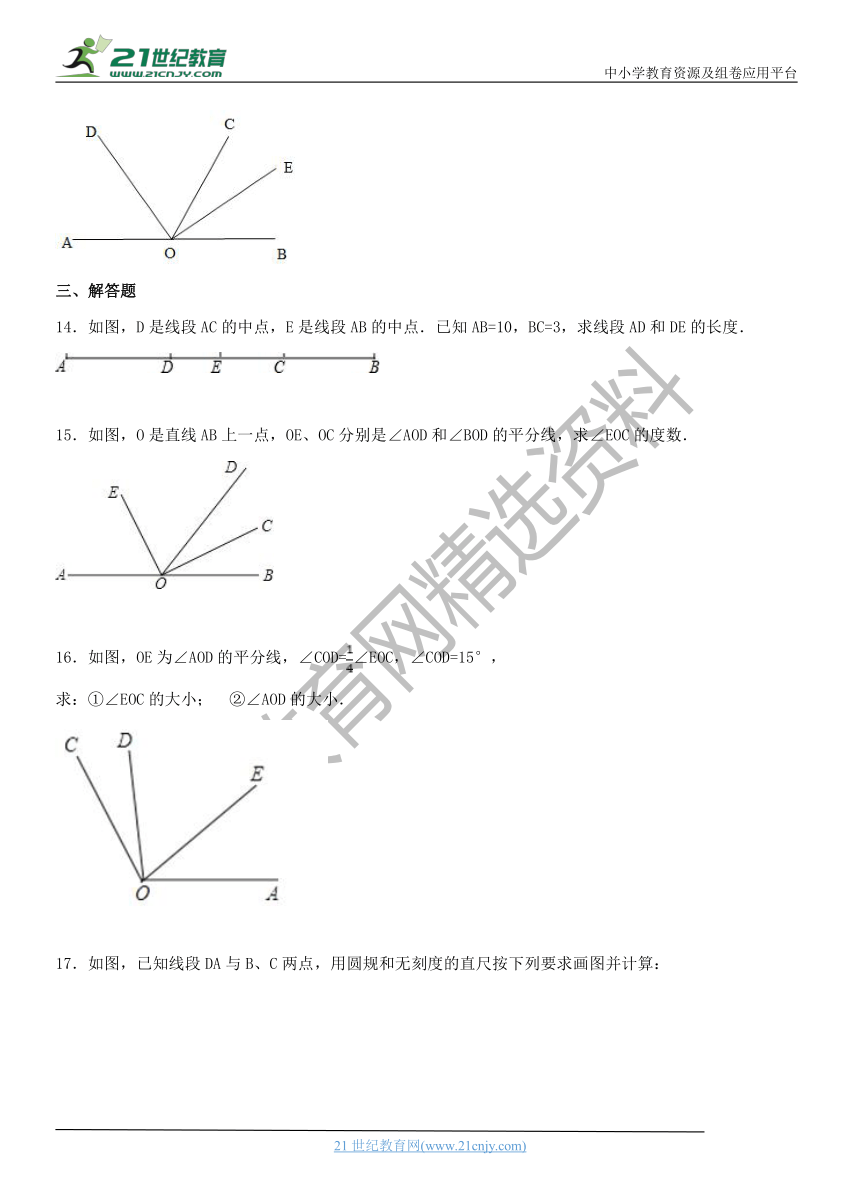
14.如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.
15.如图,O是直线AB上一点,OE、OC分别是∠AOD和∠BOD的平分线,求∠EOC的度数.
16.如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°,
求:①∠EOC的大小; ②∠AOD的大小.
17.如图,已知线段DA与B、C两点,用圆规和无刻度的直尺按下列要求画图并计算:
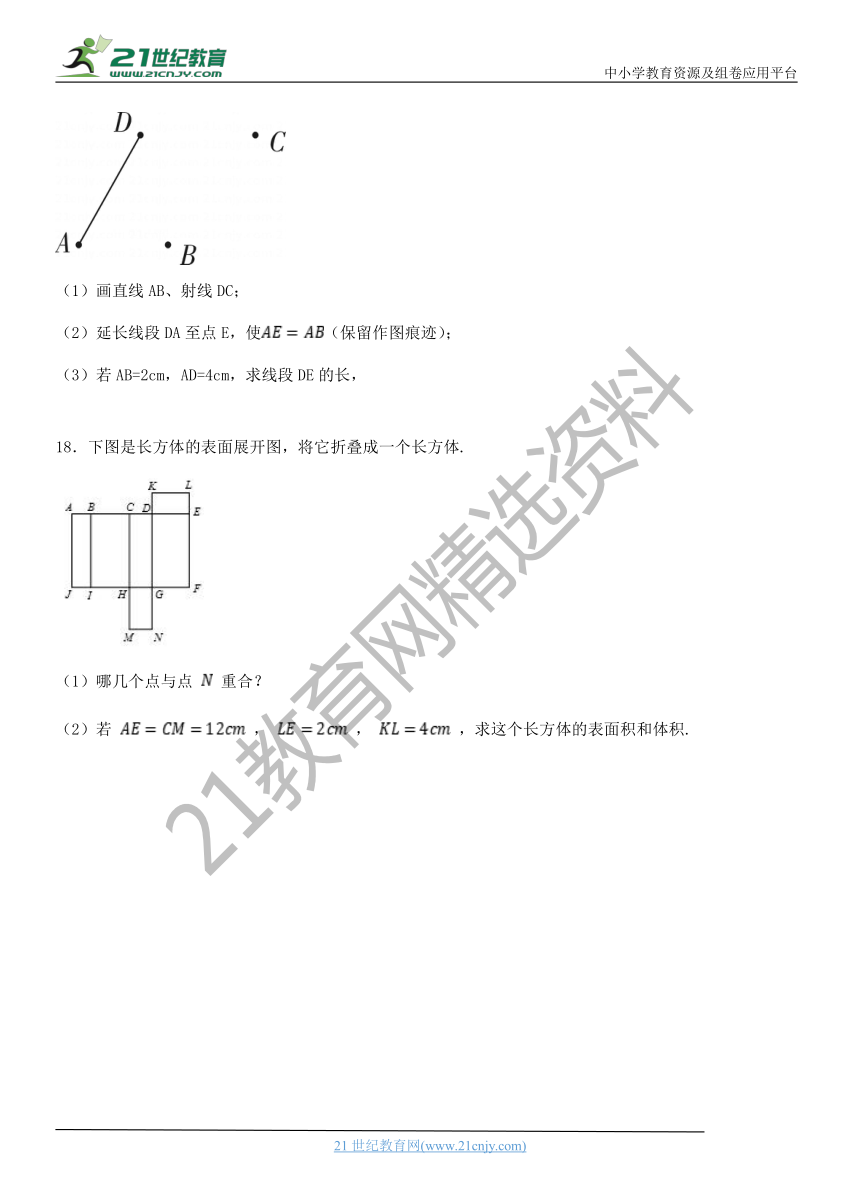
(1)画直线AB、射线DC;
(2)延长线段DA至点E,使(保留作图痕迹);
(3)若AB=2cm,AD=4cm,求线段DE的长,
18.下图是长方体的表面展开图,将它折叠成一个长方体.
(1)哪几个点与点 重合?
(2)若 , , ,求这个长方体的表面积和体积.
参考答案
1.C
2.C
3.A
4.D
5.C
6.C
7.B
8.B
9.线段
10.105
11.144°23′
12.<
13.①②③④
14.解: AB=10,BC=3
AC=AB-BC=7
∵点D为AC的中点
∴AD= AC=3.5
∵点E是AB的中点
∴AE= AB=5
∴DE=AE-AD=1.5
15.解:OE、OC分别是∠AOD和∠BOD的平分线,
∴∠DOE= ∠AOD,∠DOC= ∠DOB,
∵∠AOB=∠AOD+∠BOD=180°,
∴ (∠AOD+∠BOD)=90°,
即∠DOE+∠DOC=90°,
∴∠EOC=90°.
16.解:①由∠COD=∠EOC,得
∠EOC=4∠COD=4×15°=60°;
②由角的和差,得
∠EOD=∠EOC﹣∠COD=60°﹣15°=45°.
由角平分线的性质,得
∠AOD=2∠EOD=2×45°=90°.
17.(1)解:如图,直线、射线即为所作;
(2)解:如图,连接DA并延长,以A为圆心,AB为半径画弧与DA延长线的交点即为所作;
(3)解:∵cm
∴线段的长为.
18.解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
( )若 , , ,求这个长方体的表面积和体积.
解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 几何图形初步 单元练习 2022-2023学年人教版数学七年级上册
一、单选题
1.一个角是这个角的余角的2倍,则这个角的度数是( )
A.30° B.45° C.60° D.75°
2.已知点A,B,C在同一直线上, , ,则线段AC的长是( )
A.8cm B.2cm C.8cm或2cm D.不能确定
3.下列说法错误的是( )
A.若AC=BC,则C是线段AB的中点
B.平面内过一点有且只有一条直线与已知直线垂直
C.平行于同一直线的两条直线平行
D.一副七巧板中只有一个平行四边形,且面积大小占这副七巧板面积总和的
4.如图,下列各式中错误的是( )
A.AB=AD+DB B.CB=AB﹣AC C.CD=CB﹣DB D.AC=CB﹣DB
5.如图,已知 ,点 是 的中点,点 又是 的中点,则 ( ).
A. B. C. D.
6.如图所示,点O为直线AB上一点∠AOC=∠DOE=90°,那么图中互余角的对数为( )
A.2对 B.3对 C.4对 D.5对
7.如图,数轴上有三个点A、B、C,且A、B表示的数互为相反数,若每个单位长度表示1,则点C表示的数为( )
A.不能确定 B.-2 C.2 D.0
8.如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,∠MON等于( )
A.90° B.135° C.150° D.120°
二、填空题
9.将弯曲的河道改直,可以缩短航程,是因为:两点之间 最短
10.当时针指向2:30时,时针与分针的夹角是 度.
11.已知与互为补角,,则 .
12.如图所示的网格是正方形网格, 是网格线的交点,则 与 的大小关系为: (填“>”,“=”或“<”).
13.如图,点O在直线AB上,从点O引出射线OC,其中射线OD平分∠AOC,射线OE平分∠BOC,下列结论:①∠DOE=90°;②∠COE与∠AOE互补;③若OC平分∠BOD,则∠AOE=150°;④∠BOE的余角可表示为.其中正确的是 .(只填序号)
三、解答题
14.如图,D是线段AC的中点,E是线段AB的中点.已知AB=10,BC=3,求线段AD和DE的长度.
15.如图,O是直线AB上一点,OE、OC分别是∠AOD和∠BOD的平分线,求∠EOC的度数.
16.如图,OE为∠AOD的平分线,∠COD=∠EOC,∠COD=15°,
求:①∠EOC的大小; ②∠AOD的大小.
17.如图,已知线段DA与B、C两点,用圆规和无刻度的直尺按下列要求画图并计算:
(1)画直线AB、射线DC;
(2)延长线段DA至点E,使(保留作图痕迹);
(3)若AB=2cm,AD=4cm,求线段DE的长,
18.下图是长方体的表面展开图,将它折叠成一个长方体.
(1)哪几个点与点 重合?
(2)若 , , ,求这个长方体的表面积和体积.
参考答案
1.C
2.C
3.A
4.D
5.C
6.C
7.B
8.B
9.线段
10.105
11.144°23′
12.<
13.①②③④
14.解: AB=10,BC=3
AC=AB-BC=7
∵点D为AC的中点
∴AD= AC=3.5
∵点E是AB的中点
∴AE= AB=5
∴DE=AE-AD=1.5
15.解:OE、OC分别是∠AOD和∠BOD的平分线,
∴∠DOE= ∠AOD,∠DOC= ∠DOB,
∵∠AOB=∠AOD+∠BOD=180°,
∴ (∠AOD+∠BOD)=90°,
即∠DOE+∠DOC=90°,
∴∠EOC=90°.
16.解:①由∠COD=∠EOC,得
∠EOC=4∠COD=4×15°=60°;
②由角的和差,得
∠EOD=∠EOC﹣∠COD=60°﹣15°=45°.
由角平分线的性质,得
∠AOD=2∠EOD=2×45°=90°.
17.(1)解:如图,直线、射线即为所作;
(2)解:如图,连接DA并延长,以A为圆心,AB为半径画弧与DA延长线的交点即为所作;
(3)解:∵cm
∴线段的长为.
18.解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
( )若 , , ,求这个长方体的表面积和体积.
解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
