2015年3月山东省枣庄市峄城区左庄中学九年级数学测试试题(附答案及评分标准)
文档属性
| 名称 | 2015年3月山东省枣庄市峄城区左庄中学九年级数学测试试题(附答案及评分标准) |

|
|
| 格式 | zip | ||
| 文件大小 | 278.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 00:00:00 | ||
图片预览




文档简介
( http: / / www.21cnjy.com )
一、选择题(本大题共12个小题,每小题3分,共36分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.的倒数是( )
A.1 B. C. D.0
2.下列运算正确的是
A. B. C. D.
3.一个多边形的每个内角均为140°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
4.下列各式化简结果为无理数的是
A. B. C. D.
5.如图,AB∥CD,BC∥DE,若∠B=40°,则∠D的度数是
( http: / / www.21cnjy.com )
A.40° B.140° C.160° D.60°
6.下列几何体中,俯视图相同的是
( http: / / www.21cnjy.com )
A.① ② ③ B.① ③ ④ C.① ② ④ D.② ③ ④
7.一个正方形和两个等边三角形的位置如图所示,若∠3 = 60°,则∠1+∠2=
( http: / / www.21cnjy.com )
A.80° B.90° C.120° D.180°
8.如图,在等边△ABC中,点D、E分别是边AB、AC的中点.将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是
( http: / / www.21cnjy.com )
A.矩形 B.菱形 C.正方形 D.梯形
9.已知关于的方程,下列说法正确的是
A.当时,方程无解
B.当时,方程有两个相等的实数解
C.当时,方程有一个实数解
D.当时,方程总有两个不相等的实数解
10.我区某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是
班级 1班 2班 3班 4班 5班 6班
人数 52 60 62 54 58 62
A.平均数是60 B.中位数是59 C.极差是40 D.众数是58
11.如图,直线y=x+a-5与双曲线y=交于A,B两点,则当线段AB的长度取最小值时,a的值为
( http: / / www.21cnjy.com )
A.0 B.1 C.2 D.5
12.如图,梯形ABCD中,AD∥BC,AB=3,BC=4,连结BD,∠BAD的平分线交BD于 点E,且AE∥CD,则AD的长为
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
二、填空题(本大题共5个小题,每小题3分,共15分)请把每小题的答案填在答题卡的相应位置上.
13.计算:=______________.
14.不等式组的整数解是___________.
15.分式方程的解是___________.
16.小明在某风景区的观景台O处观测到东北方向的P处有一艘货船, 该船正向南匀速航 行,30分钟后再观察时,该船已航行到O的南偏东30,且与O相距6km的Q处.如图所示.货船的航行速度是____________km/h.(结果用根号表示.)
( http: / / www.21cnjy.com )
17.如图,在矩形ABCD中,AB=16 ( http: / / www.21cnjy.com )cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过_____________秒时,线段PQ的长是10cm.
( http: / / www.21cnjy.com )
三、解答题(本大题共9个小题,共69分)解答应写出文字说明,证明过程或演算步骤,并将解答过程写在答题卡上每小题对应的答题区域内.
18.(本题5分)
先化简,再求值:,其中是方程的根.
19.(本题6分)某省为解决农村饮用水问题 ( http: / / www.21cnjy.com ),省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
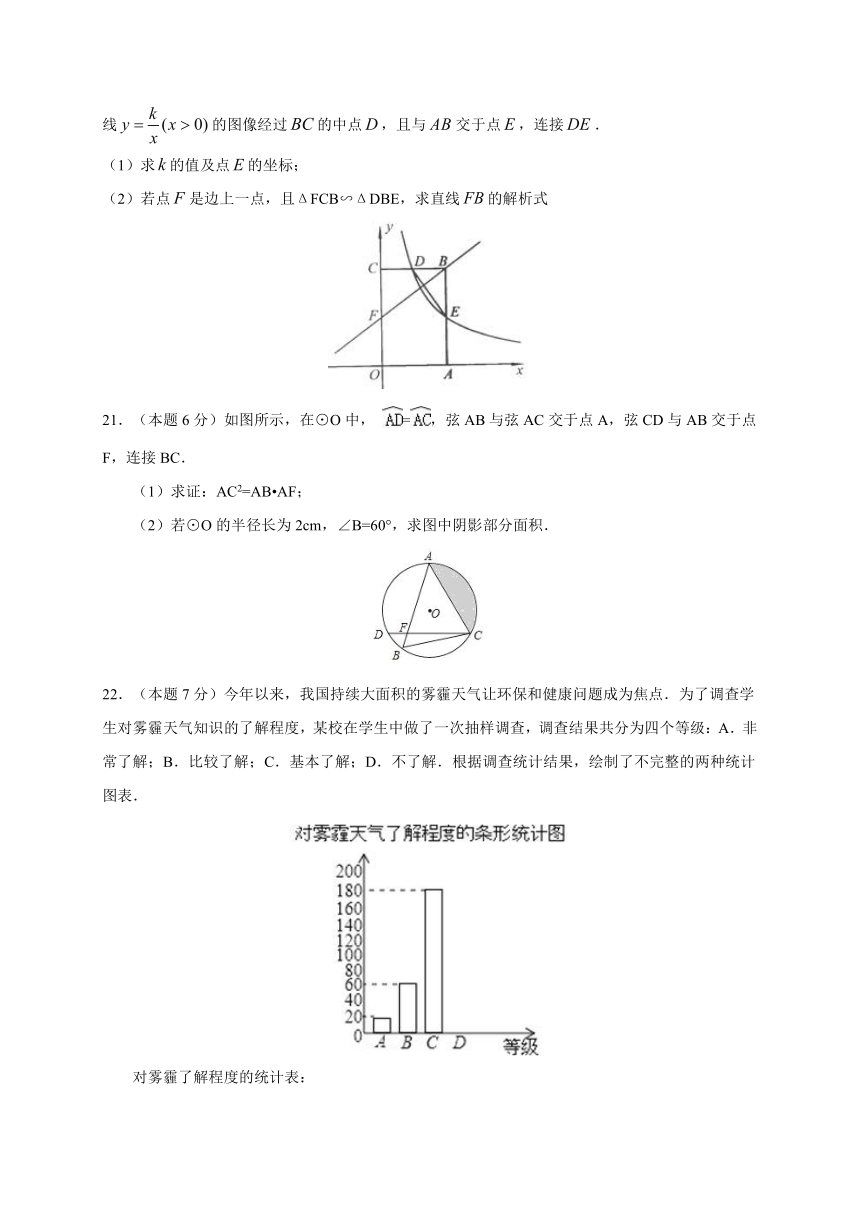
20.(本题6分)如图,矩形的顶点分别在轴和轴上,点的坐标为.双曲线的图像经过的中点,且与交于点,连接.
(1)求的值及点的坐标;
(2)若点是边上一点,且ΔFCB∽ΔDBE,求直线的解析式
( http: / / www.21cnjy.com )
(本题6分)如图所示,在⊙O中, =,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
(1)求证:AC2=AB AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
( http: / / www.21cnjy.com )
(本题7分)今年以来,我国持续大面积的雾霾 ( http: / / www.21cnjy.com )天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的两种统计图表.
( http: / / www.21cnjy.com )
对雾霾了解程度的统计表:
对雾霾的了解程度 百分比
A.非常了解 5%
B.比较了解 m
C.基本了解 45%
D.不了解 n
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)请补全图中所示数的条形统计图;
(3)根据调查结果, ( http: / / www.21cnjy.com )学校准备开展关于雾霾知识竞赛,某班要从“非常了解”等级中的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,记下数字后放回袋中,另一人再从袋中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
23.(本题6分)如图,在RtΔABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.
(1)求证DE⊥AB;
(2)如果∠FCB==∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.
( http: / / www.21cnjy.com )
24.(本题10分)某市自来水公司为了 ( http: / / www.21cnjy.com )鼓励市民节约用水,于2014年4月开始采用以用户为单位按月分段收费办法收取水费,新按月分段收费标准如下:
标准一:每月用水不超过20吨(包括20吨)的水量,每吨收费2.45元;
标准二:每月用水超过20吨但不超过30吨的水量,按每吨元收费;
标准三:超过30吨的部分,按每吨(+1.62)元收费。(说明:>2.45).
(1)居民甲4月份用水25吨,交水费65.4元,求 的值;
(2)若居民甲2014年4月以后,每月用水(吨),应交水费(元),求与之间的函数关系式,并注明自变量x的取值范围;
(3)随着夏天的到来,各家的用 ( http: / / www.21cnjy.com )水量在不但增加.为了节省开支,居民甲计划自家6月份的水费不能超过家庭月收入的2%(居民甲家的月收入为6540元),则居民甲家六月份最多能用水多少吨?
25.(本题11分)如图,在正方形 ( http: / / www.21cnjy.com )ABCD中, AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
( http: / / www.21cnjy.com )
26.(本题12分)如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与轴相切于点C,与轴交于A,B两点,∠ACD=90°,抛物线经过A,B,C三点.
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
选择题(每小题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A B C B A B B D A
二、填空题:(每小题3分,共15分)
13.,; 14.﹣2,﹣1,0; 15.;16.;17.或8;
三、解答题:(共9个小题,共69分)
18.(本题5分)
( http: / / www.21cnjy.com )
19.(本题6分)
解:(1)设求A市投资“改水工程”费用的年平均增长率为,得,
…………………………2分
解之得,,(不合题意,舍去) …………………3分
∴
答:A市投资“改水工程”费用的年平均增长率为20%. ……………………4分
(2)由题意得,
600+600(1+)+864 …………………………5分
=600+600×120%+864
=2184(万元)
答:从2012年到2014年,A市三年共投资“改水工程”2184万元.……6分
20.(本题6分)
解:(1)在矩形OABC中,
∵B点坐标为,∴边中点的坐标为(1,3)
又∵双曲线的图像经过点∴,∴ …………………2分
∵点在上,∴点的横坐标为2.
又∵经过点, ∴点纵坐标为,
∴点纵坐标为 …………………………3分
( http: / / www.21cnjy.com )
(2)由(1)得,,
∵△FBC∽△DEB,∴,即。
∴,∴,即点的坐标为 …………………………4分
设直线的解析式为,而直线经过
∴,解得 …………………………5分
∴直线的解析式为 …………………………6分
21.(本题6分)
解答:(1)证明:∵=,
∴∠ACD=∠ABC,又∠BAC=∠CAF,…………………………1分
∴△ACF∽△ABC, …………………………2分
∴,即AC2=AB AF; …………………………3分
(2)解:连接OA,OC,过O作OE⊥AC,垂足为点E,
∵∠ABC=60°,∴∠AOC=120°,
又OA=OC, ∴∠AOE=∠COE=×120°=60°,
在Rt△AOE中,OA=2cm,
∴OE=OAcos60°=1cm,………………4分
∴AE=cm,
∴AC=2AE=2cm, …………………………5分
则S阴影=S扇形OAC﹣S△AOC=cm2.…………6分
22.(本题7分)
解:(1)400; 20% ; 25%. …………………………3分
(2)图略.(说明: D,不了解的人数有100人) …………………………4分
(3)由题意画树状图如下:
所有等可能的结果共有16种:2,3,4,5,3,4,5,6,4,5,6,7,5,6,7,8.…………………5分
其中和为奇数的共有8种,
小明去的概率为,小刚去的概率也是.…………………………6分
所以这个游戏规则公平. …………………………7分
23.(本小题6分)证明:(1)连接AE,
( http: / / www.21cnjy.com )
∵∠BAC=90°,BE=EC,
∴AE=BE=BC ……………………1分
又∵DA=AB,
∴DE垂直平分AB,即DE⊥AB.…………………………2分
(2)∵∠DBC=90°
∴∠DBA+∠ABC=90°
∵DA=AB,∴∠DBA=∠DAB,
∵∠FBC=∠DAB
∴∠FBC+∠ABC=90°
∵∠AGE=90°
∴BF∥DE …………………………3分
又∵∠FBC=∠FCB,
∴FB=FC
∵BE=EC,∴FE⊥BC
∴∠DBE=∠BEF=90°
∴DB∥EF …………………………4分
∴四边形DBFE是平行四边形 …………………………5分
∴DH=FH. …………………………6分
24.(本题10分)
解:(1)由题意得,
20×2.45+5=65.4
解之得,=3.28 …………………………2分
(2)由题意得
当0≤≤20时,;…………………………3分
当20<≤30时,;…… 4分
当>30时,
= …………………………5分
即 …………………………6分
(3)6540×2%=130.8 …………………………7分
∵20×2.45=49;49+10×3.28=81.8
而49﹤81.8﹤130.8 …………………………8分
∴居民甲家6月份用水超过30吨,设他家6月用水吨,得,
-65.2≤130.8 …………………………9分
解得,≤40
答:居民甲家计划6月份最多用水40吨 .…………………………10分
25.(本题11分)(1)证明:过点F作FH⊥BE于点H,
( http: / / www.21cnjy.com )
∵四边形ABCD是正方形,
∴∠ABC=∠PHF=∠DCB=90 ,AB=BC,
∴∠BAP+∠APB=90
∵AP⊥PF,
∴∠APB+∠FPH=90
∴∠FPH=∠BAP
又∵AP=PF
∴△BAP≌△HPF ………………1分
∴PH=AB,BP=FH
∴PH=BC
∴BP+PC=PC+CH
∴CH=BP=FH ………………2分
而∠FHC=90 .∴∠FCH=CFH=45
∴∠DCF=90 -45 =45
∴∠GCF=∠FCE ………………………3分
(2)PG=PB+DG ……………………………………4分
证明:延长PB至K,使BK=DG,
∵四边形ABCD是正方形
∴AB=AD, ∠ABK=ADG=90
∴△ABK≌△ADG …………………………5分
∴AK=AG, ∠KAB=∠GAD,
而∠APF=90 ,AP=PF
∴∠PAF=∠PFA=45
∴∠BAP+∠KAB=∠KAP=45 =∠PAF
∴△KAP≌△GAP ………………………………6分
∴KP=PG,
∴KB+BP=DG+BP=PG
即,PG=PB+DG; …………………………7分
(3)存在.
如图,在直线AB上取一点M,使四边形DMPF是平行四边形,
则MD∥PF,且MD=FP,……………………8分
又∵PF=AP,
∴MD=AP
∵四边形ABCD是正方形,
∴AB=AD,∠ABP=∠DAM
∴△ABP≌△DAM …………9分
∴AM=BP=2,
∴BM=AB-AM=5-2=3. …………10分
∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形.…………11分
26.(本题12分)(1)证明:如图,连接MC,
( http: / / www.21cnjy.com )
∵⊙M与轴相切于点C,∴CM⊥OC,
∴∠MCO=90°, …………1分
又∵∠ACD=90°
∴AD为⊙M的直径,
∵DM=CM, ∠ACD+∠ADC=90°
∴∠MCD=∠MDC, ……………………2分
∵∠OCA+∠ACM=∠OCM=90°
∴∠MCD+∠ACM=90°
∴∠OCA=∠MCD=∠MDC
∵∠OCA+∠OAC=90°
∴∠OAC=∠CAD; ……………………3分
(2)解:如图,过点M作MN⊥OB于点N,
由(1)可知,AD是⊙M的直径,
∴∠ABD=90°
∵MN⊥AB, ∴∠MNA=90°
∴MN∥BD ……………………4分
∴ ……………………5分
∵∠OCM=∠CON=∠MNO=90°
∴四边形COMN为矩形,
∴MN=CO=4
∴BD=2MN=8 ……………………………………6分
(3)解:抛物线的对称轴上存在点P,使ΔPBC是以BC为腰的等腰三角形.
在⊙M中,弧AC=弧AC,∴∠ADC=∠ABC,
由(1)知,∠ADC=∠OCA,
∴∠OCA=∠OBC
在Rt△CAO和Rt△BOC中,
tan∠OCA=
∴tan∠OBC=
∴OB=2OC=8
∴A(2,0),B(8,0)
∵抛物线经过A,B两点,
∴A,B关于抛物线的对称轴对称,其对称轴为直线:;…………8分
当CP=CB=5时,△PCB为等腰三角形,
在Rt△COB中,
如图,在Rt△CM中,
80-25=55
,
∴…………………………9分
同理可求的坐标是 …………10分
当BP=BC=5时,△PCB为等腰三角形,
∴ …………5分 …………11分
同理可得坐标为
∴符合条件的点P有四个,坐标分别为,,,.…………………………………………12分
( http: / / www.21cnjy.com )
一、选择题(本大题共12个小题,每小题3分,共36分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
1.的倒数是( )
A.1 B. C. D.0
2.下列运算正确的是
A. B. C. D.
3.一个多边形的每个内角均为140°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
4.下列各式化简结果为无理数的是
A. B. C. D.
5.如图,AB∥CD,BC∥DE,若∠B=40°,则∠D的度数是
( http: / / www.21cnjy.com )
A.40° B.140° C.160° D.60°
6.下列几何体中,俯视图相同的是
( http: / / www.21cnjy.com )
A.① ② ③ B.① ③ ④ C.① ② ④ D.② ③ ④
7.一个正方形和两个等边三角形的位置如图所示,若∠3 = 60°,则∠1+∠2=
( http: / / www.21cnjy.com )
A.80° B.90° C.120° D.180°
8.如图,在等边△ABC中,点D、E分别是边AB、AC的中点.将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是
( http: / / www.21cnjy.com )
A.矩形 B.菱形 C.正方形 D.梯形
9.已知关于的方程,下列说法正确的是
A.当时,方程无解
B.当时,方程有两个相等的实数解
C.当时,方程有一个实数解
D.当时,方程总有两个不相等的实数解
10.我区某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是
班级 1班 2班 3班 4班 5班 6班
人数 52 60 62 54 58 62
A.平均数是60 B.中位数是59 C.极差是40 D.众数是58
11.如图,直线y=x+a-5与双曲线y=交于A,B两点,则当线段AB的长度取最小值时,a的值为
( http: / / www.21cnjy.com )
A.0 B.1 C.2 D.5
12.如图,梯形ABCD中,AD∥BC,AB=3,BC=4,连结BD,∠BAD的平分线交BD于 点E,且AE∥CD,则AD的长为
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
二、填空题(本大题共5个小题,每小题3分,共15分)请把每小题的答案填在答题卡的相应位置上.
13.计算:=______________.
14.不等式组的整数解是___________.
15.分式方程的解是___________.
16.小明在某风景区的观景台O处观测到东北方向的P处有一艘货船, 该船正向南匀速航 行,30分钟后再观察时,该船已航行到O的南偏东30,且与O相距6km的Q处.如图所示.货船的航行速度是____________km/h.(结果用根号表示.)
( http: / / www.21cnjy.com )
17.如图,在矩形ABCD中,AB=16 ( http: / / www.21cnjy.com )cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过_____________秒时,线段PQ的长是10cm.
( http: / / www.21cnjy.com )
三、解答题(本大题共9个小题,共69分)解答应写出文字说明,证明过程或演算步骤,并将解答过程写在答题卡上每小题对应的答题区域内.
18.(本题5分)
先化简,再求值:,其中是方程的根.
19.(本题6分)某省为解决农村饮用水问题 ( http: / / www.21cnjy.com ),省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
20.(本题6分)如图,矩形的顶点分别在轴和轴上,点的坐标为.双曲线的图像经过的中点,且与交于点,连接.
(1)求的值及点的坐标;
(2)若点是边上一点,且ΔFCB∽ΔDBE,求直线的解析式
( http: / / www.21cnjy.com )
(本题6分)如图所示,在⊙O中, =,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
(1)求证:AC2=AB AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
( http: / / www.21cnjy.com )
(本题7分)今年以来,我国持续大面积的雾霾 ( http: / / www.21cnjy.com )天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的两种统计图表.
( http: / / www.21cnjy.com )
对雾霾了解程度的统计表:
对雾霾的了解程度 百分比
A.非常了解 5%
B.比较了解 m
C.基本了解 45%
D.不了解 n
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)请补全图中所示数的条形统计图;
(3)根据调查结果, ( http: / / www.21cnjy.com )学校准备开展关于雾霾知识竞赛,某班要从“非常了解”等级中的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,记下数字后放回袋中,另一人再从袋中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
23.(本题6分)如图,在RtΔABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.
(1)求证DE⊥AB;
(2)如果∠FCB==∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.
( http: / / www.21cnjy.com )
24.(本题10分)某市自来水公司为了 ( http: / / www.21cnjy.com )鼓励市民节约用水,于2014年4月开始采用以用户为单位按月分段收费办法收取水费,新按月分段收费标准如下:
标准一:每月用水不超过20吨(包括20吨)的水量,每吨收费2.45元;
标准二:每月用水超过20吨但不超过30吨的水量,按每吨元收费;
标准三:超过30吨的部分,按每吨(+1.62)元收费。(说明:>2.45).
(1)居民甲4月份用水25吨,交水费65.4元,求 的值;
(2)若居民甲2014年4月以后,每月用水(吨),应交水费(元),求与之间的函数关系式,并注明自变量x的取值范围;
(3)随着夏天的到来,各家的用 ( http: / / www.21cnjy.com )水量在不但增加.为了节省开支,居民甲计划自家6月份的水费不能超过家庭月收入的2%(居民甲家的月收入为6540元),则居民甲家六月份最多能用水多少吨?
25.(本题11分)如图,在正方形 ( http: / / www.21cnjy.com )ABCD中, AB=5,P是BC边上任意一点,E是BC延长线上一点,连接AP,作PF⊥AP,使PF=PA,连接CF,AF,AF交CD边于点G,连接PG.
(1)求证:∠GCF=∠FCE;
(2)判断线段PG,PB与DG之间的数量关系,并证明你的结论;
(3)若BP=2,在直线AB上是否存在一点M,使四边形DMPF是平行四边形,若存在,求出BM的长度,若不存在,说明理由.
( http: / / www.21cnjy.com )
26.(本题12分)如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与轴相切于点C,与轴交于A,B两点,∠ACD=90°,抛物线经过A,B,C三点.
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
选择题(每小题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A B C B A B B D A
二、填空题:(每小题3分,共15分)
13.,; 14.﹣2,﹣1,0; 15.;16.;17.或8;
三、解答题:(共9个小题,共69分)
18.(本题5分)
( http: / / www.21cnjy.com )
19.(本题6分)
解:(1)设求A市投资“改水工程”费用的年平均增长率为,得,
…………………………2分
解之得,,(不合题意,舍去) …………………3分
∴
答:A市投资“改水工程”费用的年平均增长率为20%. ……………………4分
(2)由题意得,
600+600(1+)+864 …………………………5分
=600+600×120%+864
=2184(万元)
答:从2012年到2014年,A市三年共投资“改水工程”2184万元.……6分
20.(本题6分)
解:(1)在矩形OABC中,
∵B点坐标为,∴边中点的坐标为(1,3)
又∵双曲线的图像经过点∴,∴ …………………2分
∵点在上,∴点的横坐标为2.
又∵经过点, ∴点纵坐标为,
∴点纵坐标为 …………………………3分
( http: / / www.21cnjy.com )
(2)由(1)得,,
∵△FBC∽△DEB,∴,即。
∴,∴,即点的坐标为 …………………………4分
设直线的解析式为,而直线经过
∴,解得 …………………………5分
∴直线的解析式为 …………………………6分
21.(本题6分)
解答:(1)证明:∵=,
∴∠ACD=∠ABC,又∠BAC=∠CAF,…………………………1分
∴△ACF∽△ABC, …………………………2分
∴,即AC2=AB AF; …………………………3分
(2)解:连接OA,OC,过O作OE⊥AC,垂足为点E,
∵∠ABC=60°,∴∠AOC=120°,
又OA=OC, ∴∠AOE=∠COE=×120°=60°,
在Rt△AOE中,OA=2cm,
∴OE=OAcos60°=1cm,………………4分
∴AE=cm,
∴AC=2AE=2cm, …………………………5分
则S阴影=S扇形OAC﹣S△AOC=cm2.…………6分
22.(本题7分)
解:(1)400; 20% ; 25%. …………………………3分
(2)图略.(说明: D,不了解的人数有100人) …………………………4分
(3)由题意画树状图如下:
所有等可能的结果共有16种:2,3,4,5,3,4,5,6,4,5,6,7,5,6,7,8.…………………5分
其中和为奇数的共有8种,
小明去的概率为,小刚去的概率也是.…………………………6分
所以这个游戏规则公平. …………………………7分
23.(本小题6分)证明:(1)连接AE,
( http: / / www.21cnjy.com )
∵∠BAC=90°,BE=EC,
∴AE=BE=BC ……………………1分
又∵DA=AB,
∴DE垂直平分AB,即DE⊥AB.…………………………2分
(2)∵∠DBC=90°
∴∠DBA+∠ABC=90°
∵DA=AB,∴∠DBA=∠DAB,
∵∠FBC=∠DAB
∴∠FBC+∠ABC=90°
∵∠AGE=90°
∴BF∥DE …………………………3分
又∵∠FBC=∠FCB,
∴FB=FC
∵BE=EC,∴FE⊥BC
∴∠DBE=∠BEF=90°
∴DB∥EF …………………………4分
∴四边形DBFE是平行四边形 …………………………5分
∴DH=FH. …………………………6分
24.(本题10分)
解:(1)由题意得,
20×2.45+5=65.4
解之得,=3.28 …………………………2分
(2)由题意得
当0≤≤20时,;…………………………3分
当20<≤30时,;…… 4分
当>30时,
= …………………………5分
即 …………………………6分
(3)6540×2%=130.8 …………………………7分
∵20×2.45=49;49+10×3.28=81.8
而49﹤81.8﹤130.8 …………………………8分
∴居民甲家6月份用水超过30吨,设他家6月用水吨,得,
-65.2≤130.8 …………………………9分
解得,≤40
答:居民甲家计划6月份最多用水40吨 .…………………………10分
25.(本题11分)(1)证明:过点F作FH⊥BE于点H,
( http: / / www.21cnjy.com )
∵四边形ABCD是正方形,
∴∠ABC=∠PHF=∠DCB=90 ,AB=BC,
∴∠BAP+∠APB=90
∵AP⊥PF,
∴∠APB+∠FPH=90
∴∠FPH=∠BAP
又∵AP=PF
∴△BAP≌△HPF ………………1分
∴PH=AB,BP=FH
∴PH=BC
∴BP+PC=PC+CH
∴CH=BP=FH ………………2分
而∠FHC=90 .∴∠FCH=CFH=45
∴∠DCF=90 -45 =45
∴∠GCF=∠FCE ………………………3分
(2)PG=PB+DG ……………………………………4分
证明:延长PB至K,使BK=DG,
∵四边形ABCD是正方形
∴AB=AD, ∠ABK=ADG=90
∴△ABK≌△ADG …………………………5分
∴AK=AG, ∠KAB=∠GAD,
而∠APF=90 ,AP=PF
∴∠PAF=∠PFA=45
∴∠BAP+∠KAB=∠KAP=45 =∠PAF
∴△KAP≌△GAP ………………………………6分
∴KP=PG,
∴KB+BP=DG+BP=PG
即,PG=PB+DG; …………………………7分
(3)存在.
如图,在直线AB上取一点M,使四边形DMPF是平行四边形,
则MD∥PF,且MD=FP,……………………8分
又∵PF=AP,
∴MD=AP
∵四边形ABCD是正方形,
∴AB=AD,∠ABP=∠DAM
∴△ABP≌△DAM …………9分
∴AM=BP=2,
∴BM=AB-AM=5-2=3. …………10分
∴当BM=3,BM+AM=AB时,四边形DMPF是平行四边形.…………11分
26.(本题12分)(1)证明:如图,连接MC,
( http: / / www.21cnjy.com )
∵⊙M与轴相切于点C,∴CM⊥OC,
∴∠MCO=90°, …………1分
又∵∠ACD=90°
∴AD为⊙M的直径,
∵DM=CM, ∠ACD+∠ADC=90°
∴∠MCD=∠MDC, ……………………2分
∵∠OCA+∠ACM=∠OCM=90°
∴∠MCD+∠ACM=90°
∴∠OCA=∠MCD=∠MDC
∵∠OCA+∠OAC=90°
∴∠OAC=∠CAD; ……………………3分
(2)解:如图,过点M作MN⊥OB于点N,
由(1)可知,AD是⊙M的直径,
∴∠ABD=90°
∵MN⊥AB, ∴∠MNA=90°
∴MN∥BD ……………………4分
∴ ……………………5分
∵∠OCM=∠CON=∠MNO=90°
∴四边形COMN为矩形,
∴MN=CO=4
∴BD=2MN=8 ……………………………………6分
(3)解:抛物线的对称轴上存在点P,使ΔPBC是以BC为腰的等腰三角形.
在⊙M中,弧AC=弧AC,∴∠ADC=∠ABC,
由(1)知,∠ADC=∠OCA,
∴∠OCA=∠OBC
在Rt△CAO和Rt△BOC中,
tan∠OCA=
∴tan∠OBC=
∴OB=2OC=8
∴A(2,0),B(8,0)
∵抛物线经过A,B两点,
∴A,B关于抛物线的对称轴对称,其对称轴为直线:;…………8分
当CP=CB=5时,△PCB为等腰三角形,
在Rt△COB中,
如图,在Rt△CM中,
80-25=55
,
∴…………………………9分
同理可求的坐标是 …………10分
当BP=BC=5时,△PCB为等腰三角形,
∴ …………5分 …………11分
同理可得坐标为
∴符合条件的点P有四个,坐标分别为,,,.…………………………………………12分
( http: / / www.21cnjy.com )
同课章节目录
