1.1探索勾股定理

课件45张PPT。探索勾股定理 (1)教学目标：知识目标：
（１）经历用拼图法验证勾股定理的过程，进一步理解掌握勾股定理；
（２）了解勾股定理的历史，初步掌握勾股定理的简单应用。
能力目标：
经历观察、归纳、猜想和验证的数学发现过程，发展合情合理的推理能力，沟通数学知识之间的内在联系，体会形数结合的思想；
情感目标：
（１）通过对勾股定理历史的了解和实例应用，体会勾股定理的文化价值。
（２）通过获得成功的经验和克服困难的经历，增进数学学习的信心。
教学重、难点的确定
关注学生是否能与同伴进行有效的合作交流；
关注学生是否积极的进行思考；
关注学生能否探索出解决问题的方法。教学重、难点：
重点：通过拼图验证勾股定理及勾股定理的应用过程，使学生获得一些研究问题与合作交流的方法经验。
难点：利用数形结合的方法验证勾股定理。教学方法的选择：数学知识、数学思想和方法必须由学生在现实的数学活动实践中理解和发展；
教学中，以学生为本位，充分挖掘教材的空间，为学生搭建动手实践、自主探索、合作交流的平台；
注重让学生经历数学知识的形成过程，充分调动学生的学习积极性，并通过这个过程，使学生体验学习成功的乐趣，在积极的思维中获取知识，发展能力。知识反映出来的技能、能力、方法、德育等因素： 本节知识通过 “ 拼图实践—探索验证—
分析结果—运用定理 ” 等活动过程，使学生
进一步理解勾股定理，并从中学会思考，
学会探索，学会运用，学会交流，体会知
识反映出来的丰富的文化内涵，指导学生
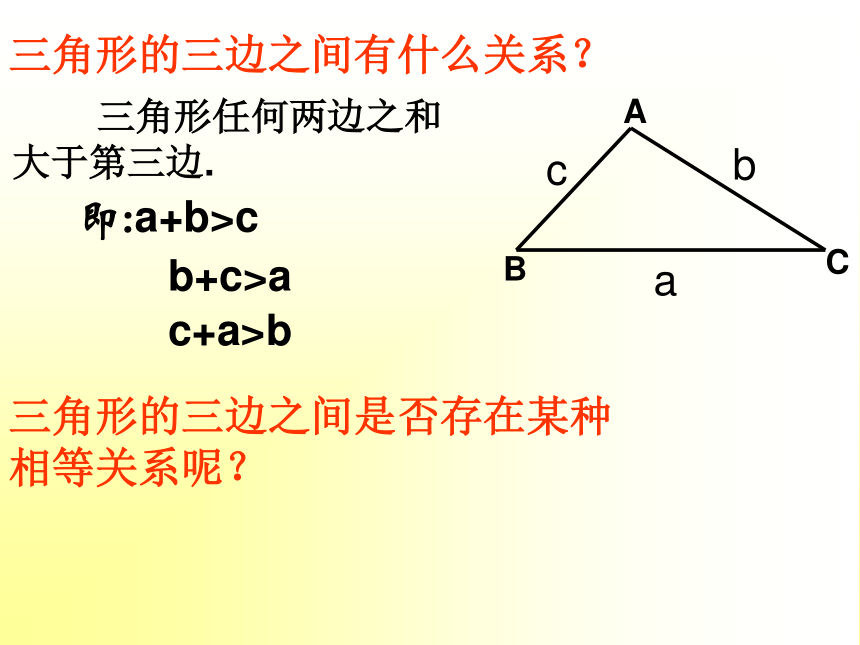
认识现实世界中蕴涵着的数学信息。 即:a+b>cb+c>ac+a>b 三角形任何两边之和
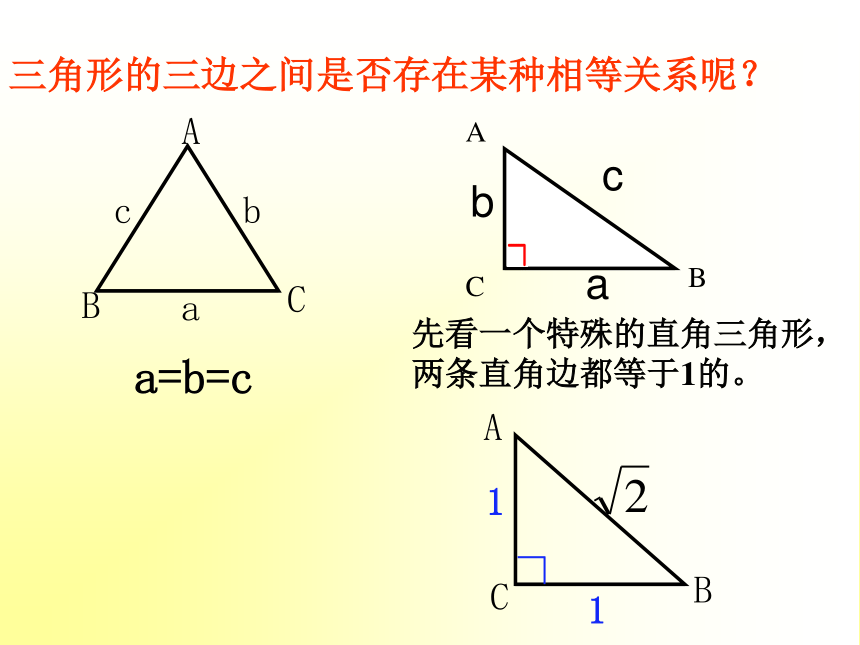
大于第三边.三角形的三边之间有什么关系？三角形的三边之间是否存在某种相等关系呢？先看一个特殊的直角三角形，
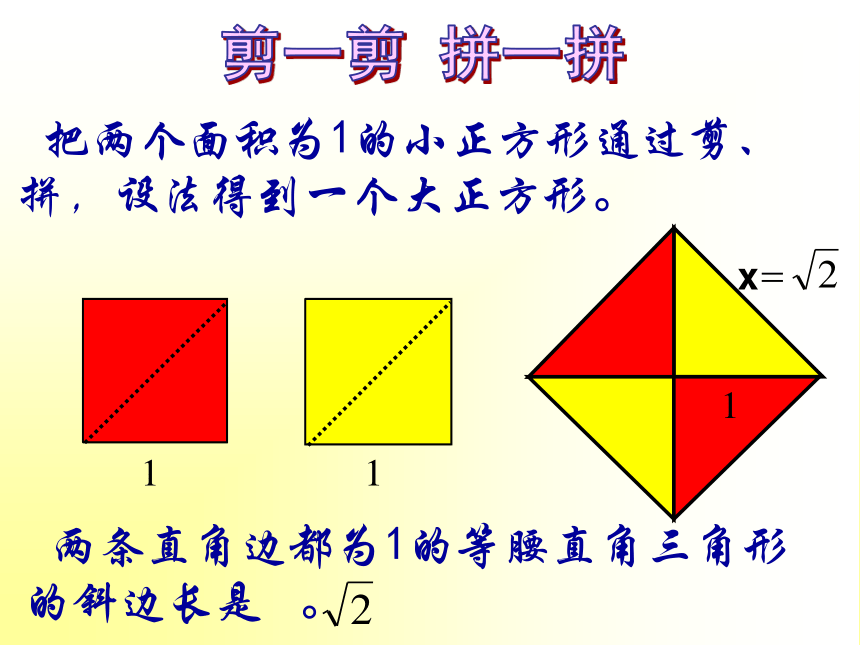
两条直角边都等于1的。三角形的三边之间是否存在某种相等关系呢？a=b=c11 两条直角边都为1的等腰直角三角形的斜边长是 。剪一剪 拼一拼 把两个面积为1的小正方形通过剪、拼，设法得到一个大正方形。
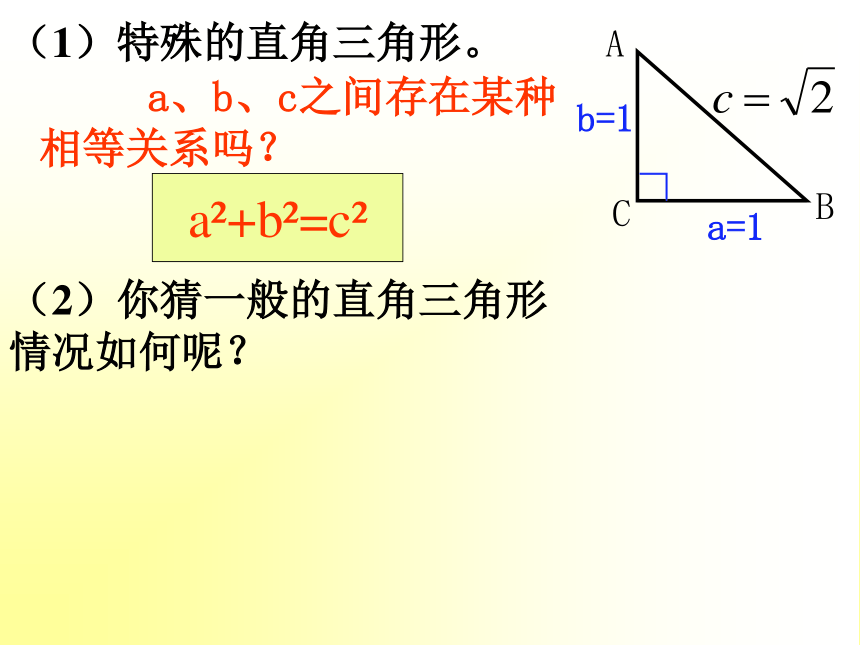
x111b=1a=1 a、b、c之间存在某种相等关系吗？（1）特殊的直角三角形。（2）你猜一般的直角三角形
情况如何呢？a2+b2=c2做一做 画一个直角三角形，使两条直角边分别等于：
（1）3cm和4cm。
（2）5cm和12cm。
然后用刻度尺量出斜边的长。a、b、c之间存在某种相等关系吗？ 在Rt△ABC中，∠C=900 ，
则有 a2+b2=c2。猜想： 直角三角形两直角边的
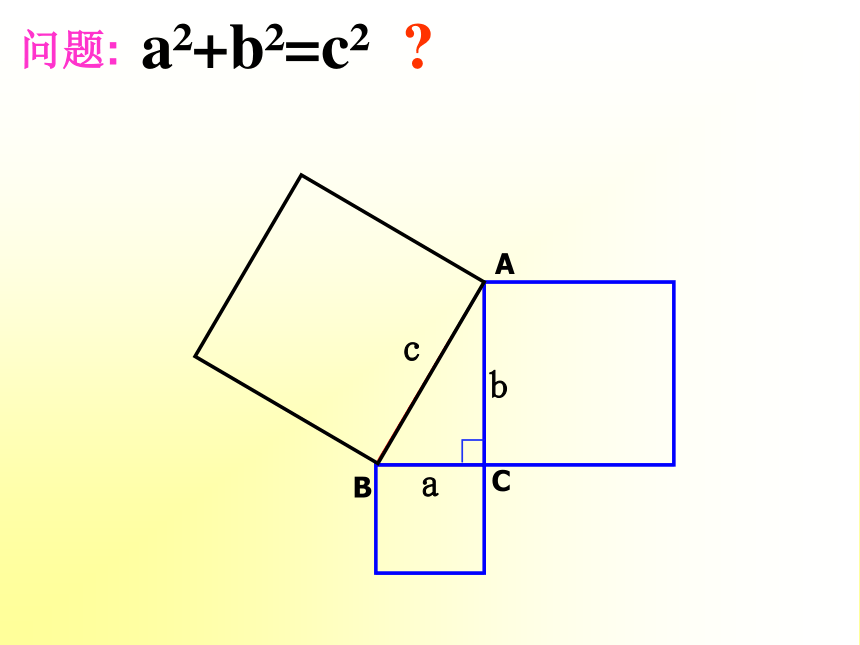
平方和等于斜边的平方.即：问题:ABCａｃｂ∟a2+b2=c2 ?ABCａｂ∟问题:a2+b2=c2 ?ｃｃ 都拼成了边长为(a+b)的正方形。=由a2+b2你还会想到什么 ?c2+2ab=(a+b)2c2+2ab=a2+2ab+b2∴a2+b2=c2问题:拼图方案二ｂｂｂｂｃｃｃｃａａａａ(b-a)2+2ab=c2b2 -2ab+a2+2ab=c2∴a2+b2=c2赵爽弦图美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，
就把这一证法称为“总统”证法。 有趣的总统证法aabbcc 利用两个直角三角形
验证勾股定理┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理ACB在Rt△ABC中，∠C=900 ，欣赏体会，丰富自我
向学生展示勾股定理的有关史料．
让学生更好地体会勾股定理的丰富内涵与文化背景，陶冶情操，丰富自我，从中得到深层次的发展． 相传2500年前，有一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系。　　数学家毕达哥拉斯的发现：A、B、C的面积有什么关系？直角三角形三边有什么关系？SA+SB=SC两直边的平方和等于斜边的平方abca2+b2=c2 勾股定理在西方被称为毕达哥拉斯定理，
相传是古希腊数学家兼哲学家毕达哥拉斯于
公元前550年首先发现的。其实，我国古代
人民对这一数学定理的发现和应用，远比毕
达哥拉斯早得多。在公元前1100年左右的西
周时期，比毕达哥拉斯要早了五百多年。?? 中国古代的数学家们不仅很早就发现并
应用勾股定理，而且很早就尝试对勾股定理
作理论上的证明。最早对勾股定理进行证明
的，是三国时期吴国的数学家赵爽。赵爽弦图 读一读
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就.
　　　　　　　 图1-1图1-21.求下列直角三角形中未知边的长:a=8b=?c=17b=16c=20a=?b=12a=5c=?做一做ACBACBACB解：在Rt△ABC中，∠C=90°
a2 + b2 =c2根据勾股定理，得∴b2 = c2- a2 =172 -82
=225解得b= ±15∵b >0∴b =15小试牛刀（1）在Rt△ABC中，∠C=90°,a=3，b=4，
求c 的值.
（2）在Rt△ABC中，∠B=90°，a=3，b=4，
求c的值.解：在Rt△ABC中，∠C=90°
a2 + b2 =c2根据勾股定理，得∴b2 = c2- a2 =172 -82
=225解得b= ±15∵b >0∴b =15 例 .在Rt△ABC中，∠Ｃ=90°.
(1) 已知：a=6，ｂ=8，求c；　
(2) 已知：a=40，c=41，求b；
(3) 已知：c=13，b=5，求a；
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结一定要慎重哦！2、若一个直角三角形的三边长分别
为3，4， x，则x＝　　　　　 . 做一做一定要仔细审题哦！3、若一个三角形的三边长分别
为3，4， x，则x　　　　　 . 做一做1这节课你学到了什么知识？小 结：3、你还有什么疑惑或没有弄懂的地方？2 运用“勾股定理”应注意什么问题？作业：1.探索勾股定理的其它验证方法。2.收集勾股定理的证明方法,
写一篇关于勾股定理的小论文。再见结论变形 直角三角形中，两直角边的平方和等于斜边的平方；
c2=a2 + b2小试牛刀1、已知Rt△ABC中，∠C=90°.
①若a = 5，b = 12，则c= 　　　；
②若c= 10，b = 8，则a = .
③若a=2，c=6，则b= 。一定要慎重哦！2、若一个直角三角形的三边长分别
为3，4， x，则x＝　　　　　 . 如图，大风将一根木制旗杆吹裂，随时都可能倒下，十分危急。现在需要划出一个安全警戒区域，那么你能确定这个安全区域的半径至少是多少米吗？议一议：9m24m例2：将长为5.41米的梯子AC斜靠在墙上，
BC长为2.16米，求梯子上端A到墙的底端
B的距离AB（精确到0.01米）CAB∵ a2+b2 =c2
∴ S1=S2+S32、探究下面三个圆面积之间的关系作业：

1、用勾股定理知识设计一个图案
2、已知三角形三边为5、6、7，求
△ABC面积.小结：
　　
　作业：1.了解用面积法证明直角三角形勾股定理

2.理解并掌握勾股定理:两直角边的平方和等于 斜边的平方,即a2+b2=c2
3.能将勾股定理灵活变形,学会用勾股定理解
直角三角形：已知两边求第三边的问 题以及
有关面积问题
P.87 1.2.3. P.88 5.6. ???