高中数学课件 必修一:3方程的根与函数的零点
文档属性
| 名称 | 高中数学课件 必修一:3方程的根与函数的零点 |  | |
| 格式 | zip | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-01 14:54:27 | ||
图片预览




文档简介
课件18张PPT。§3.1.1方程的根与函数的零点 1.一元一次函数y=ax+b(a≠0)
函数图像是_________.
2.一元二次函数y=ax2+bx+c(a≠0)
当a>0时图象开口________ ;
当a<0时图象开口________ ;
其顶点坐标为____________;
对称轴为直线____________.
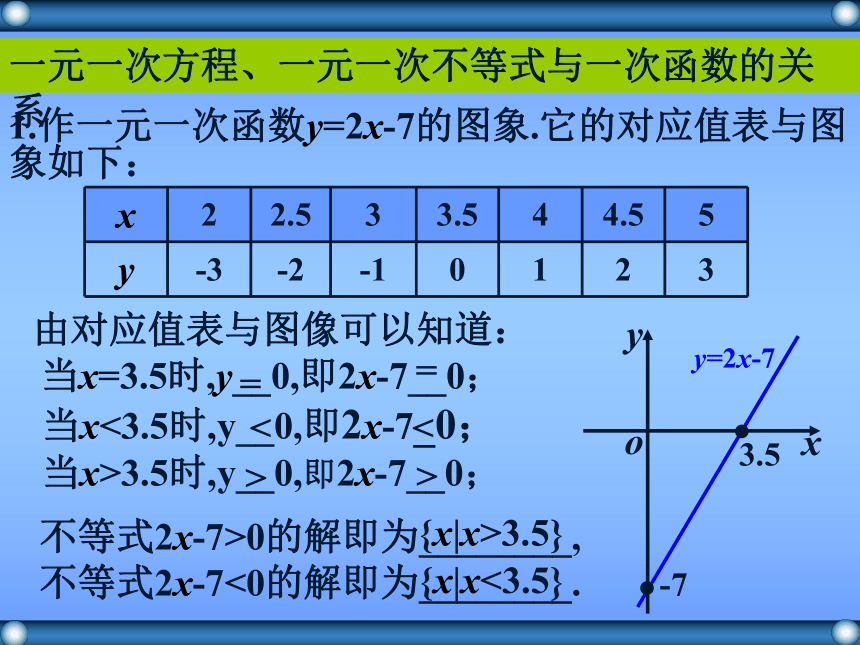
向上向下一条直线准备知识1.作一元一次函数y=2x-7的图象.它的对应值表与图象如下:由对应值表与图像可以知道:
当x=3.5时,y__0,即2x-7__0;
当x<3.5时,y__0,即2x-7_0;
当x>3.5时,y__0,即2x-7__0;不等式2x-7>0的解即为________,
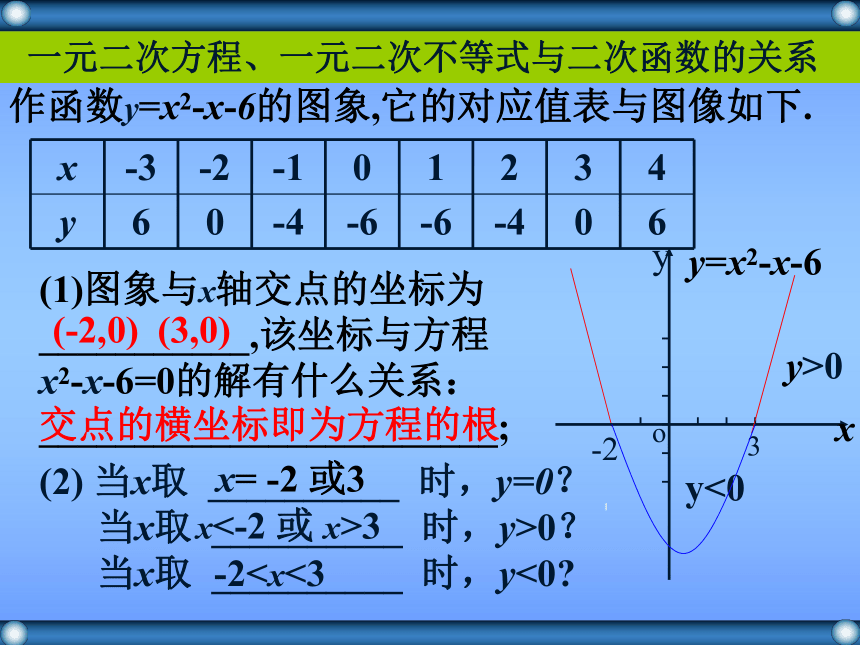
不等式2x-7<0的解即为________.{x|x<3.5}{x|x>3.5}==>><<一元一次方程、一元一次不等式与一次函数的关系2.通过以上分析,得出以下结论(1)图象与x轴交点的坐标为___________,该坐标与方程 x2-x-6=0的解有什么关系:________________________;(2) 当x取 __________ 时,y=0?
当x取 __________ 时,y>0?
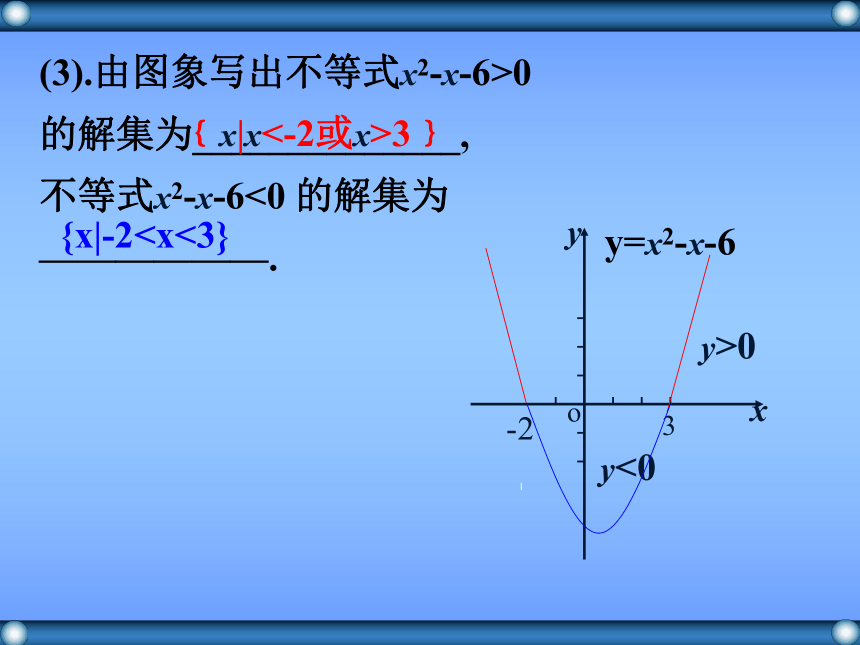
当x取 __________ 时,y<0? 交点的横坐标即为方程的根-23y>0y<0yxo(-2,0) (3,0)x= -2 或3x<-2 或 x>3-20 的解集为______________,
不等式x2-x-6<0 的解集为
——————.﹛x|x<-2或x>3﹜{x|-20y<0yxoy=x2-x-6(一)引入:一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c (a≠0)的图象有什么关系?(1)方程x2-2x-3=0与函数y=x2-2x-3(2)方程x2-2x+1=0与函数y=x2-2x+1(3)方程x2-2x+3=0与函数y=x2-2x+3几何画板 容易知道,方程x2-2x-3=0有两个实数根x1=-1,x2=3;函数y=x2-2x-3的图象与x轴有两个交点(-1,0),(3,0),这样,方程x2-2x-3=0的两个实数根就是函数y=x2-2x-3的图象与轴的交点的横坐标. 方程x2-2x+3=0无实数根,函数y=x2-2x+3的图象与x轴没有交点.x1x2⊿=b2-4ac二次函数 y=ax2+bx+c(a>0)
的图象方程ax2+bx+c=0(a>0) 的根 x1(x2)⊿>0⊿=0⊿<0
两个不
等实根两个零点两个相等实根无实根一个
零点函数y=ax2+bx+c(a>0) 的零点无零点二次函数的零点个数与相应二次方程的实根个数的关系设判别式Δ=b2-4ac,我们有:(1)当Δ>0时,一元二次方程有两个不等的实数根x1,x2,相应的二次函数的图象与x轴有两个交点(x1,0),(x2,0).(2)当Δ=0时,一元二次方程有两个相等实数根x1=x2 ,相应的二次函数的图象与x轴有唯一的交点(x1,0).(3)当Δ<0时,一元二次方程没有实数根,相应的二次函数的图象与x轴没有的交点.方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点 1.函数的零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point).注意:并不是所有的函数都有零点.例如函数y=2,y=x2+1不存在零点.2.方程的根与函数的零点的关系 即 函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴交点的横坐标. 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·.f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.3.函数零点的存在性的判定方法ab例1 求证:一元二次方程2x2+3x-7=0有两个不相等的实数根证明:因为Δ=32- 4×2×(-7)=65>0,所以方程2x2+3x-7=0有两个不等实根.证明: 设f(x)=2x2+3x-7,因为函数的图象是一条开口向上的抛物线,且f(0)=2×02+3×0-7=-7<0,所以函数f(x)的图象与x轴有两个不同的交点,即方程2x2+3x-7=0有两个不相等的实数根.证法(一):判别式法证法(二):函数零点的存在性的判定方法例2 判断方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2.解:考虑函数f(x)=(x-2)(x-5)-1,f(5)=-1,f(2)=-1.又因为f(x)的图象是开口向上的抛物线,所以抛物线与横轴在(5,+∞)内有一个交点,在(-∞,2)内也有一个交点. 所以方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2.点击进入几何画板例3 已知函数f(x)=3x-x2,问:方程f(x)=0在区间[-1,0]内有没有实数解?点击进入几何画板例4 求函数f(x)=lnx+2x-6的零点个数.解:用计算器或计算机作出x、f(x)的对应值表和图象. 由表和图可知,f(2)<0,f(3)>0,即f(2) ·f(3)<0,说明这个函数在区间内有零点.由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.点击进入几何画板作业 练习:P.88 (2),(4).
P.92 2.再见山东省临沂一中 李福国 退出
函数图像是_________.
2.一元二次函数y=ax2+bx+c(a≠0)
当a>0时图象开口________ ;
当a<0时图象开口________ ;
其顶点坐标为____________;
对称轴为直线____________.
向上向下一条直线准备知识1.作一元一次函数y=2x-7的图象.它的对应值表与图象如下:由对应值表与图像可以知道:
当x=3.5时,y__0,即2x-7__0;
当x<3.5时,y__0,即2x-7_0;
当x>3.5时,y__0,即2x-7__0;不等式2x-7>0的解即为________,
不等式2x-7<0的解即为________.{x|x<3.5}{x|x>3.5}==>><<一元一次方程、一元一次不等式与一次函数的关系2.通过以上分析,得出以下结论(1)图象与x轴交点的坐标为___________,该坐标与方程 x2-x-6=0的解有什么关系:________________________;(2) 当x取 __________ 时,y=0?
当x取 __________ 时,y>0?
当x取 __________ 时,y<0? 交点的横坐标即为方程的根-23y>0y<0yxo(-2,0) (3,0)x= -2 或3x<-2 或 x>3-2
不等式x2-x-6<0 的解集为
——————.﹛x|x<-2或x>3﹜{x|-2
的图象方程ax2+bx+c=0(a>0) 的根 x1(x2)⊿>0⊿=0⊿<0
两个不
等实根两个零点两个相等实根无实根一个
零点函数y=ax2+bx+c(a>0) 的零点无零点二次函数的零点个数与相应二次方程的实根个数的关系设判别式Δ=b2-4ac,我们有:(1)当Δ>0时,一元二次方程有两个不等的实数根x1,x2,相应的二次函数的图象与x轴有两个交点(x1,0),(x2,0).(2)当Δ=0时,一元二次方程有两个相等实数根x1=x2 ,相应的二次函数的图象与x轴有唯一的交点(x1,0).(3)当Δ<0时,一元二次方程没有实数根,相应的二次函数的图象与x轴没有的交点.方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点 1.函数的零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point).注意:并不是所有的函数都有零点.例如函数y=2,y=x2+1不存在零点.2.方程的根与函数的零点的关系 即 函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴交点的横坐标. 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·.f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.3.函数零点的存在性的判定方法ab例1 求证:一元二次方程2x2+3x-7=0有两个不相等的实数根证明:因为Δ=32- 4×2×(-7)=65>0,所以方程2x2+3x-7=0有两个不等实根.证明: 设f(x)=2x2+3x-7,因为函数的图象是一条开口向上的抛物线,且f(0)=2×02+3×0-7=-7<0,所以函数f(x)的图象与x轴有两个不同的交点,即方程2x2+3x-7=0有两个不相等的实数根.证法(一):判别式法证法(二):函数零点的存在性的判定方法例2 判断方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2.解:考虑函数f(x)=(x-2)(x-5)-1,f(5)=-1,f(2)=-1.又因为f(x)的图象是开口向上的抛物线,所以抛物线与横轴在(5,+∞)内有一个交点,在(-∞,2)内也有一个交点. 所以方程(x-2)(x-5)=1有两个相异的实数解,且一个大于5,一个小于2.点击进入几何画板例3 已知函数f(x)=3x-x2,问:方程f(x)=0在区间[-1,0]内有没有实数解?点击进入几何画板例4 求函数f(x)=lnx+2x-6的零点个数.解:用计算器或计算机作出x、f(x)的对应值表和图象. 由表和图可知,f(2)<0,f(3)>0,即f(2) ·f(3)<0,说明这个函数在区间内有零点.由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.点击进入几何画板作业 练习:P.88 (2),(4).
P.92 2.再见山东省临沂一中 李福国 退出
