新人教A版选择性必修第二册2023年秋高中数学第四章 数列 章末综合测评(含解析)
文档属性
| 名称 | 新人教A版选择性必修第二册2023年秋高中数学第四章 数列 章末综合测评(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 136.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 16:59:02 | ||
图片预览



文档简介
章末综合测评(一) 数列
(时间:120分钟 满分:150分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知数列1,,3,,…,,…,则是这个数列的( )
A.第10项 B.第11项
C.第12项 D.第21项
2.已知数列{an},an=2n+1,Sn为其前n项和,则点(n,Sn)在下列________函数的图象上( )
A B
C D
3.在等差数列{an}中,已知a4+a8=16,则该数列第6项a6=( )
A.6 B.8
C.12 D.16
4.在等比数列{an}中,已知a4a7=8,a2a5a6=24,则a2=( )
A.6 B.4
C.3 D.2
5.大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,它是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是0,2,4,8,12,18,24,32,40,50,…,则该数列第18项为( )
A.200 B.162
C.144 D.128
6.设{an}是公差不为0的等差数列,a1=2,且a1,a3,a6成等比数列,则{an}的前n项和Sn=( )
A.+ B.+
C.+ D.n2+n
7.已知数列{an}满足a1=,an+1=(n∈N*),则a2 022=( )
A.-1 B.
C.+1 D.2
8.数列{an}是正项等比数列,满足anan+1=4n,则数列的前n项和Tn=( )
A. B.
C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.在等比数列{an}中,a5=4,a7=16,则a6可以为( )
A.8 B.12
C.-8 D.-12
10.满足下列条件的数列{an}(n∈N*)是递增数列的为( )
A.an= B.an=n2+n
C.an=1-2n D.an=2n+1
11.在等差数列{an}中,a66<0,a67>0,且a67>|a66|,Sn为数列{an}的前n项和,则( )
A.公差d<0
B.a66+a67<0
C.S131<0
D.使Sn>0的n的最小值为132
12.已知两个等差数列和的前n项和分别为Sn和Tn,且=,则使得为整数的正整数n的值为( )
A.2 B.3
C.4 D.14
三、填空题(本题共4小题,每小题5分,共20分,将答案填在题中横线上)
13.若等比数列{an}的前n项和Sn=m·4n-1+t(其中m,t是常数),则=________.
14.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”.其中“日减功迟”的具体含义是每天比前一天少织同样多的布,则每天比前一天少织布的尺数为________.
15.记Sn为等差数列{an}的前n项和,若a1=-2,a2+a6=2,则S10=________.
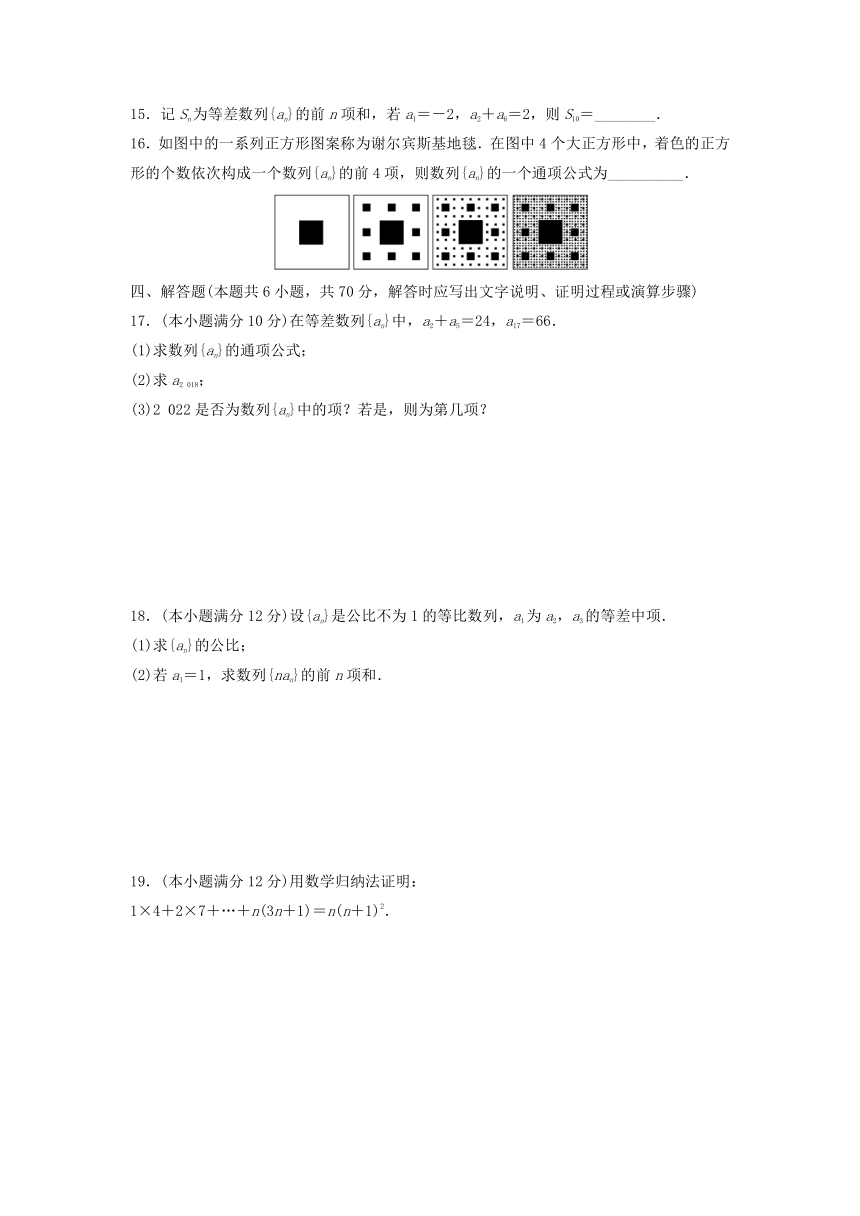
16.如图中的一系列正方形图案称为谢尔宾斯基地毯.在图中4个大正方形中,着色的正方形的个数依次构成一个数列{an}的前4项,则数列{an}的一个通项公式为__________.
四、解答题(本题共6小题,共70分,解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)在等差数列{an}中,a2+a5=24,a17=66.
(1)求数列{an}的通项公式;
(2)求a2 018;
(3)2 022是否为数列{an}中的项?若是,则为第几项?
18.(本小题满分12分)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n项和.
19.(本小题满分12分)用数学归纳法证明:
1×4+2×7+…+n(3n+1)=n(n+1)2.
20.(本小题满分12分)已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4.
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
(2)求{an}和{bn}的通项公式.
21.(本小题满分12分) (2021·全国乙卷)设{an}是首项为1的等比数列,数列{bn}满足bn=.已知a1,3a2,9a3成等差数列.
(1)求{an}和{bn}的通项公式;
(2)记Sn和Tn分别为{an}和{bn}的前n项和.证明:Tn<.
22.(本小题满分12分)某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2 000万元,将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始,每年年底上缴资金d万元,并将剩余资金全部投入下一年生产.设第n年年底企业上缴资金后的剩余资金为an万元.
(1)用d表示a1,a2,并写出an+1与an的关系式;
(2)若公司希望经过m(m≥3)年使企业的剩余资金为4 000万元,试确定企业每年上缴资金d的值(用m表示).
章末综合测评(一)
1.B [观察可知
项公式为an=(事实上,根号内的数成等差数列,首项为1,公差为2),令21=2n-1,解得n=11,故选B.]
2.C [由等差数列的求和公式可得Sn===n2+2n,
所以点(n,Sn)在函数y=x2+2x上.]
3.B [因为数列{an}是等差数列,由等差数列的性质得2a6=a4+a8=16,所以a6=8.故选B.]
4.C [由题设可得 a1q=3,由此可得a2=3,故应选C.]
5.B [偶数项分别为2,8,18,32,50,即2×1,2×4,2×9,2×16,2×25,即偶数项对应的通项公式为a2n=2n2,则数列的第18项为第9个偶数,即a18=a2×9=2×92=2×81=162.]
6.A [设公差为d,则a1(a1+5d)=(a1+2d)2,把a1=2代入可解得d=.∴an=2+(n-1)×=n+.∴Sn==n2+.故选A.]
7.C [因为a1=,
an+1=(n∈N*),
所以a2=a1-1=-1,a3===+1,a4=a3-1=,a5=a4-1=-1,
a6==+1,…所以数列{an}的周期为3,
因为2 022=3×674,
所以a2 022=a3=+1.]
8.A [数列{an}是正项等比数列,公比设为q(q>0),由anan+1=4n,可得a1a2=q=4,a2a3=q3=16,解得a1=,q=2,则an=a1qn-1=·2n-1=.
则=
==
=2,
则Tn=2
=2=.故选A.]
9.AC [∵==q2 q=±2,当q=2时,a6=a5q=4×2=8,
当q=-2时,a6=a5q=4×(-2)=-8,故选AC.]
10.BD [根据题意,依次分析选项:对于A,an=,a1=1,a2=,不是递增数列,不符合题意;对于B,an=n2+n,an-an-1=n2+n-(n-1)2-(n-1)=2n>0,是递增数列,符合题意;对于C,an=1-2n,an-an-1=(1-2n)-[1-2(n-1)]=-2,不是递增数列,不符合题意;对于D,an=2n+1,函数y=2x+1为递增函数,则an=2n+1是递增数列,符合题意.]
11.CD [因为a66<0,a67>0,且a67>|a66|,
所以d>0,a67>-a66,即a67+a66>0,
所以S132=66(a1+a132)=66(a66+a67)>0,
S131==131a66<0,
所以使Sn>0的n的最小值为132.]
12.ACD [由题意可得===,则====3+,
由于为整数,则n+1为15的正约数,则n+1的可能取值有3,5,15,
因此,正整数n的可能取值有2,4,14.故选ACD.]
13.-4 [Sn=m·4n-1+t=·m·4n+t,因为{an}为等比数列,∴t=-m,∴=-4.]
14. [设第n天织布的尺数为an,可知数列为等差数列,设等差数列的公差为d,前n项和为Sn,则a1=5,an=1,Sn=90,
则Sn==3n=90,解得n=30,∴a30=a1+29d=5+29d=1,解得d=-,因此,每天比前一天少织布的尺数为.]
15.25 [法一:设等差数列{an}的公差为d,则由a2+a6=2得a1+d+a1+5d=2,即-4+6d=2,解得d=1,所以S10=10×(-2)+×1=25.
法二:设等差数列{an}的公差为d,因为a2+a6=2a4=2,所以a4=1,所以d===1,所以S10=10×(-2)+×1=25.]
16.an= [根据题中图形可知,a1=1,an+1-an=8n,
当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+8+82+…+8n-1=.]
17.解: (1)因为等差数列{an}中,a2+a5=24,a17=66.
所以
解得a1=2,d=4,所以an=4n-2.
(2)由(1)可得a2 018=8 070.
(3)令an=4n-2=2 022,所以n=506,
所以2 022是数列{an}中的第506项.
18.解: (1)设{an}的公比为q,由题设得2a1=a2+a3,
即2a1=a1q+a1q2.
所以q2+q-2=0,解得q=1(舍去)或q=-2.
故{an}的公比为-2.
(2)记Sn为{nan}的前n项和.由(1)及题设可得,an=(-2)n-1.
所以Sn=1+2×(-2)+…+n×(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)×(-2)n-1+n×(-2)n.
可得3Sn=1+(-2)+(-2)2+…+(-2)n-1-n×(-2)n=-n×(-2)n.
所以Sn=-.
19.解: (1)当n=1时,左边=1×4=4,
右边=1×22=4,所以等式成立.
(2)假设当n=k时命题成立,即
1×4+2×7+…+k(3k+1)=k(k+1)2,
那么,当n=k+1时,1×4+2×7+…+k(3k+1)+(k+1)(3k+4)=k(k+1)2+(k+1)(3k+4)=(k+1)[(k+1)+1]2,即n=k+1时,命题成立,
由(1)(2)知等式对任意的n∈N*均成立.
20.解: (1)[证明]由题设得4(an+1+bn+1)=2(an+bn),即an+1+bn+1=(an+bn).
又因为a1+b1=1,所以{an+bn}是首项为1,公比为的等比数列.
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以{an-bn}是首项为1,公差为2的等差数列.
(2)由(1)知,an+bn=,an-bn=2n-1.
所以an=[(an+bn)+(an-bn)]=+n-,
bn=[(an+bn)-(an-bn)]=-n+.
21.解: (1)设{an}的公比为q,则an=qn-1.
因为a1,3a2,9a3成等差数列,所以1+9q2=2×3q,
解得q=,
故an=,bn=.
(2)证明: 由(1)知Sn==,
Tn=+++…+ ①,
Tn=+++…++ ②,
①-②得Tn=+++…+-,
即Tn=-=-,
整理得Tn=-,
则2Tn-Sn=2-=-<0,
故Tn<.
22.解: (1)由题意得a1=2 000(1+50%)-d=3 000-d,a2=a1(1+50%)-d=a1-d=4 500-d,
an+1=an(1+50%)-d=an-d.
(2)由(1)得an=an-1-d=-d=·an-2-d-d=…=a1-d.
整理得an=(3 000-d)-2d=·(3 000-3d)+2d.
由题意知am=4 000,所以(3 000-3d)+2d=4 000,
解得d==.
故该企业每年上缴资金d的值为万元时,经过m(m≥3)年企业的剩余资金为4 000万元.
(时间:120分钟 满分:150分)
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知数列1,,3,,…,,…,则是这个数列的( )
A.第10项 B.第11项
C.第12项 D.第21项
2.已知数列{an},an=2n+1,Sn为其前n项和,则点(n,Sn)在下列________函数的图象上( )
A B
C D
3.在等差数列{an}中,已知a4+a8=16,则该数列第6项a6=( )
A.6 B.8
C.12 D.16
4.在等比数列{an}中,已知a4a7=8,a2a5a6=24,则a2=( )
A.6 B.4
C.3 D.2
5.大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,它是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是0,2,4,8,12,18,24,32,40,50,…,则该数列第18项为( )
A.200 B.162
C.144 D.128
6.设{an}是公差不为0的等差数列,a1=2,且a1,a3,a6成等比数列,则{an}的前n项和Sn=( )
A.+ B.+
C.+ D.n2+n
7.已知数列{an}满足a1=,an+1=(n∈N*),则a2 022=( )
A.-1 B.
C.+1 D.2
8.数列{an}是正项等比数列,满足anan+1=4n,则数列的前n项和Tn=( )
A. B.
C. D.
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.在等比数列{an}中,a5=4,a7=16,则a6可以为( )
A.8 B.12
C.-8 D.-12
10.满足下列条件的数列{an}(n∈N*)是递增数列的为( )
A.an= B.an=n2+n
C.an=1-2n D.an=2n+1
11.在等差数列{an}中,a66<0,a67>0,且a67>|a66|,Sn为数列{an}的前n项和,则( )
A.公差d<0
B.a66+a67<0
C.S131<0
D.使Sn>0的n的最小值为132
12.已知两个等差数列和的前n项和分别为Sn和Tn,且=,则使得为整数的正整数n的值为( )
A.2 B.3
C.4 D.14
三、填空题(本题共4小题,每小题5分,共20分,将答案填在题中横线上)
13.若等比数列{an}的前n项和Sn=m·4n-1+t(其中m,t是常数),则=________.
14.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”.其中“日减功迟”的具体含义是每天比前一天少织同样多的布,则每天比前一天少织布的尺数为________.
15.记Sn为等差数列{an}的前n项和,若a1=-2,a2+a6=2,则S10=________.
16.如图中的一系列正方形图案称为谢尔宾斯基地毯.在图中4个大正方形中,着色的正方形的个数依次构成一个数列{an}的前4项,则数列{an}的一个通项公式为__________.
四、解答题(本题共6小题,共70分,解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)在等差数列{an}中,a2+a5=24,a17=66.
(1)求数列{an}的通项公式;
(2)求a2 018;
(3)2 022是否为数列{an}中的项?若是,则为第几项?
18.(本小题满分12分)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n项和.
19.(本小题满分12分)用数学归纳法证明:
1×4+2×7+…+n(3n+1)=n(n+1)2.
20.(本小题满分12分)已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4.
(1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
(2)求{an}和{bn}的通项公式.
21.(本小题满分12分) (2021·全国乙卷)设{an}是首项为1的等比数列,数列{bn}满足bn=.已知a1,3a2,9a3成等差数列.
(1)求{an}和{bn}的通项公式;
(2)记Sn和Tn分别为{an}和{bn}的前n项和.证明:Tn<.
22.(本小题满分12分)某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2 000万元,将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始,每年年底上缴资金d万元,并将剩余资金全部投入下一年生产.设第n年年底企业上缴资金后的剩余资金为an万元.
(1)用d表示a1,a2,并写出an+1与an的关系式;
(2)若公司希望经过m(m≥3)年使企业的剩余资金为4 000万元,试确定企业每年上缴资金d的值(用m表示).
章末综合测评(一)
1.B [观察可知
项公式为an=(事实上,根号内的数成等差数列,首项为1,公差为2),令21=2n-1,解得n=11,故选B.]
2.C [由等差数列的求和公式可得Sn===n2+2n,
所以点(n,Sn)在函数y=x2+2x上.]
3.B [因为数列{an}是等差数列,由等差数列的性质得2a6=a4+a8=16,所以a6=8.故选B.]
4.C [由题设可得 a1q=3,由此可得a2=3,故应选C.]
5.B [偶数项分别为2,8,18,32,50,即2×1,2×4,2×9,2×16,2×25,即偶数项对应的通项公式为a2n=2n2,则数列的第18项为第9个偶数,即a18=a2×9=2×92=2×81=162.]
6.A [设公差为d,则a1(a1+5d)=(a1+2d)2,把a1=2代入可解得d=.∴an=2+(n-1)×=n+.∴Sn==n2+.故选A.]
7.C [因为a1=,
an+1=(n∈N*),
所以a2=a1-1=-1,a3===+1,a4=a3-1=,a5=a4-1=-1,
a6==+1,…所以数列{an}的周期为3,
因为2 022=3×674,
所以a2 022=a3=+1.]
8.A [数列{an}是正项等比数列,公比设为q(q>0),由anan+1=4n,可得a1a2=q=4,a2a3=q3=16,解得a1=,q=2,则an=a1qn-1=·2n-1=.
则=
==
=2,
则Tn=2
=2=.故选A.]
9.AC [∵==q2 q=±2,当q=2时,a6=a5q=4×2=8,
当q=-2时,a6=a5q=4×(-2)=-8,故选AC.]
10.BD [根据题意,依次分析选项:对于A,an=,a1=1,a2=,不是递增数列,不符合题意;对于B,an=n2+n,an-an-1=n2+n-(n-1)2-(n-1)=2n>0,是递增数列,符合题意;对于C,an=1-2n,an-an-1=(1-2n)-[1-2(n-1)]=-2,不是递增数列,不符合题意;对于D,an=2n+1,函数y=2x+1为递增函数,则an=2n+1是递增数列,符合题意.]
11.CD [因为a66<0,a67>0,且a67>|a66|,
所以d>0,a67>-a66,即a67+a66>0,
所以S132=66(a1+a132)=66(a66+a67)>0,
S131==131a66<0,
所以使Sn>0的n的最小值为132.]
12.ACD [由题意可得===,则====3+,
由于为整数,则n+1为15的正约数,则n+1的可能取值有3,5,15,
因此,正整数n的可能取值有2,4,14.故选ACD.]
13.-4 [Sn=m·4n-1+t=·m·4n+t,因为{an}为等比数列,∴t=-m,∴=-4.]
14. [设第n天织布的尺数为an,可知数列为等差数列,设等差数列的公差为d,前n项和为Sn,则a1=5,an=1,Sn=90,
则Sn==3n=90,解得n=30,∴a30=a1+29d=5+29d=1,解得d=-,因此,每天比前一天少织布的尺数为.]
15.25 [法一:设等差数列{an}的公差为d,则由a2+a6=2得a1+d+a1+5d=2,即-4+6d=2,解得d=1,所以S10=10×(-2)+×1=25.
法二:设等差数列{an}的公差为d,因为a2+a6=2a4=2,所以a4=1,所以d===1,所以S10=10×(-2)+×1=25.]
16.an= [根据题中图形可知,a1=1,an+1-an=8n,
当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+8+82+…+8n-1=.]
17.解: (1)因为等差数列{an}中,a2+a5=24,a17=66.
所以
解得a1=2,d=4,所以an=4n-2.
(2)由(1)可得a2 018=8 070.
(3)令an=4n-2=2 022,所以n=506,
所以2 022是数列{an}中的第506项.
18.解: (1)设{an}的公比为q,由题设得2a1=a2+a3,
即2a1=a1q+a1q2.
所以q2+q-2=0,解得q=1(舍去)或q=-2.
故{an}的公比为-2.
(2)记Sn为{nan}的前n项和.由(1)及题设可得,an=(-2)n-1.
所以Sn=1+2×(-2)+…+n×(-2)n-1,
-2Sn=-2+2×(-2)2+…+(n-1)×(-2)n-1+n×(-2)n.
可得3Sn=1+(-2)+(-2)2+…+(-2)n-1-n×(-2)n=-n×(-2)n.
所以Sn=-.
19.解: (1)当n=1时,左边=1×4=4,
右边=1×22=4,所以等式成立.
(2)假设当n=k时命题成立,即
1×4+2×7+…+k(3k+1)=k(k+1)2,
那么,当n=k+1时,1×4+2×7+…+k(3k+1)+(k+1)(3k+4)=k(k+1)2+(k+1)(3k+4)=(k+1)[(k+1)+1]2,即n=k+1时,命题成立,
由(1)(2)知等式对任意的n∈N*均成立.
20.解: (1)[证明]由题设得4(an+1+bn+1)=2(an+bn),即an+1+bn+1=(an+bn).
又因为a1+b1=1,所以{an+bn}是首项为1,公比为的等比数列.
由题设得4(an+1-bn+1)=4(an-bn)+8,即an+1-bn+1=an-bn+2.
又因为a1-b1=1,所以{an-bn}是首项为1,公差为2的等差数列.
(2)由(1)知,an+bn=,an-bn=2n-1.
所以an=[(an+bn)+(an-bn)]=+n-,
bn=[(an+bn)-(an-bn)]=-n+.
21.解: (1)设{an}的公比为q,则an=qn-1.
因为a1,3a2,9a3成等差数列,所以1+9q2=2×3q,
解得q=,
故an=,bn=.
(2)证明: 由(1)知Sn==,
Tn=+++…+ ①,
Tn=+++…++ ②,
①-②得Tn=+++…+-,
即Tn=-=-,
整理得Tn=-,
则2Tn-Sn=2-=-<0,
故Tn<.
22.解: (1)由题意得a1=2 000(1+50%)-d=3 000-d,a2=a1(1+50%)-d=a1-d=4 500-d,
an+1=an(1+50%)-d=an-d.
(2)由(1)得an=an-1-d=-d=·an-2-d-d=…=a1-d.
整理得an=(3 000-d)-2d=·(3 000-3d)+2d.
由题意知am=4 000,所以(3 000-3d)+2d=4 000,
解得d==.
故该企业每年上缴资金d的值为万元时,经过m(m≥3)年企业的剩余资金为4 000万元.
