华师大版九年级数学上册单元测试题第23章 图形的相似 习题(含解析)
文档属性
| 名称 | 华师大版九年级数学上册单元测试题第23章 图形的相似 习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 09:07:49 | ||
图片预览




文档简介
九年级数学上册单元测试题
第23章图形的相似
一、选择题(共12题;每小题4分,共48分)
1.若,则的值为( )
A. B. C. D.
2.)已知,且a+b+c≠0,则k的值是( )
A. 2 B. 3 C. D.
3.如图,△ABC与△DEF位似,点O是它们的位似中心,且相似比为1:2,则△ABC与△DEF的周长之比是( )
A. 1:2 B. 1:4
C. 1:3 D. 1:9
4.如图,已知矩形ABCD,AD=24,CD=16,点R、P分别是DC,BC上的点,点E、F分别是AP,RP的中点,当点P在BC上从B向C移动,而点R不动时,若CR=9,则EF=( )
A. 12 B. 12.5
C. 9 D. 不能确定
5.如图,直线a∥b∥c,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB:BC=1:2,DE=3,则EF的长为( )
A. 1.5 B. 6 C. 9 D. 12
6.如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则AD=( )
A. 2 B. 1
C. D.
7.如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AD:BD的值为( )
A. 1:9 B. 1:3 C. 1:8 D. 1:2
8.比例尺为1:1000000的地图上,A、B两地间的图上距离为2厘米,则两地间的实际距离是( )千米.
A. 0.2 B. 2 C. 20 D. 200
9.如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是( )
A. 5m B. 10m C. 20m D. 40m
10.如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
A. 3.5 B. 4 C. 7 D. 14
11.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )
A. 90m B. 60m C. 100m D. 120m
12.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A. ∠ABP=∠C B. ∠APB=∠ABC
C. = D. =
二、填空题(共6题;每小题4分,共24分)
13.如图,已知直线,且,,则________.
14.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=1,则AD=_____.
15.若两个相似三角形的周长比为2:3,则它们的面积比是_____.
16.若点C是线段AB的黄金分割点,且AC=2,则AB=_____.
17.直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,已知DF=3,则AE=_____.
18.如图,D,E分别是△ABC的边AB,AC上的点,请你添加一个条件,使△ABC与△AED相似,你添加的条件是_____.
三、解答题(共8题;共78分)
19.(8分)如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
20.(8分)如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,AD=3,DP=2,CP=1,求BC的长.
21.(10分)如图,点D,E,F分别在△ABC的边AB,AC,BC上,且DE∥BC,EF∥AB.求证:=.
22.(10分)如图,在△ABC中,点D在BC边上,AD=AB,点E在AC边上,且∠DEC=∠ADB.求证:AB2=AE AC.
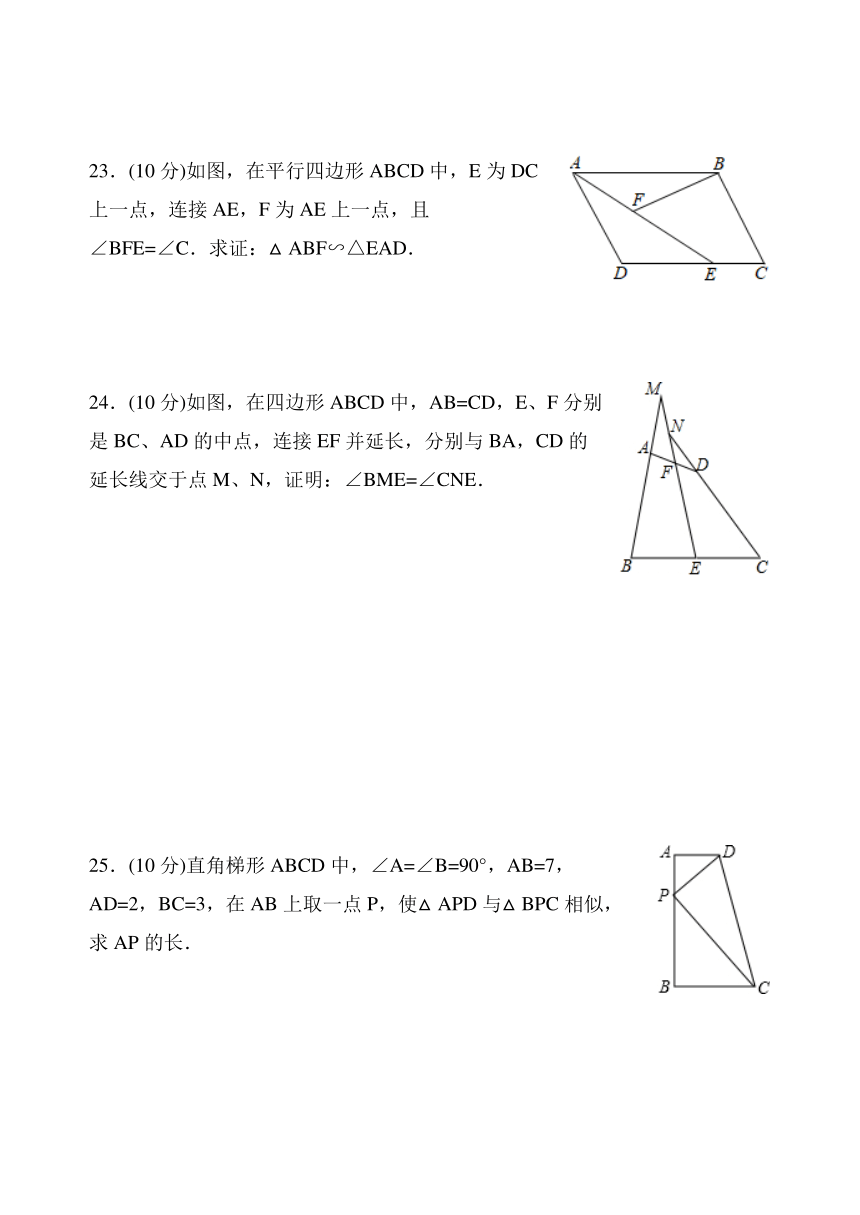
23.(10分)如图,在平行四边形ABCD中,E为DC上一点,连接AE,F为AE上一点,且∠BFE=∠C.求证:△ABF∽△EAD.
24.(10分)如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
25.(10分)直角梯形ABCD中,∠A=∠B=90°,AB=7,AD=2,BC=3,在AB上取一点P,使△APD与△BPC相似,求AP的长.
26.(12分)
(1)如图1,在中,D,E,F分别为上的点,交于点G,求证:.
(2)如图2,在(1)的条件下,连接.若,求的值.
(3)如图3,在中,与交于点O,E为上一点,交于点G,交于点F.若平分,求的长.
试卷答案
1.【答案】A
【解析】根据,可得a=,代入代数式求解即可.
解:∵,
∴a=,
∴==,
故选:A.
2.【答案】D
【解析】根据比例的基本性质,即可进行解答.
解:∵,a+b+c≠0,
∴,整理得:,
∴.
故选:D.
3.【答案】A
【解析】根据两三角形位似,周长比等于相似比即可求解.
解:∵△ABC与△DEF位似,点O是它们的位似中心,且相似比为1:2,
∴△ABC与△DEF的周长之比是1:2,
故选:A.
4.【答案】B
【解析】连接AR,根据勾股定理可求出AR,再根据中位线定理即可得出答案.
解:如图,连接AR,
∵CR=9,CD=16,
∴DR=7,
∵AD=24,∠D=90°,
∴AR==25,
∵点E、F分别是AP,RP的中点,
∴EF=AR=12.5,
故选:B.
5.【答案】B
【解析】由a∥b∥c,可得,由此即可解决问题.
解:∵a∥b∥c,
∴,
∴,
∴EF=6,
故选:B.
6.【答案】B
【解析】由∠DBC=∠A,BC=,AC=3可证明△CBD∽△CAB,由此可得,代入可求得CD,即可得到AD.
解:∵∠DBC=∠A,∠C=∠C,
∴△CBD∽△CAB,
∴,即,
∴CD=2,
∴AD=AC-CD=3-2=1.
故选:B.
7.【答案】D
【解析】证明△ADE∽△ABC,由S△ADE:S四边形DBCE=1:8,得S△ADE:S△ABC=1:9,根据相似三角形面积的比等于相似比的平方可得出答案.
解:∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=AD2:AB2,
∵S△ADE:S四边形DBCE=1:8,
∴S△ADE:S△ABC=1:9,
∴AD:AB=1:3,
∴AD:BD=1:2.
故选:D.
8.【答案】C
【解析】根据实际距离=图上距离÷比例尺.代值计算即可得出答案.
解:根据题意得:
2÷=2000000(厘米),
2000000厘米=20千米.
故选:C.
9.【答案】C
【解析】根据三角形中位线定理解答即可.
解:∵点C,D分别是OA,OB的中点,
∴AB=2CD=20(m),
故选:C.
10.【答案】A
【解析】由菱形的周长可求得AB的长,再利用三角形中位线定理可求得答案0
解:
∵四边形ABCD为菱形,
∴AB=×28=7,且O为BD的中点,
∵E为AD的中点,
∴OE为△ABD的中位线,
∴OE=AB=3.5,
故选:A.
11.【答案】A
【解析】先证明△ABD∽△ECD,然后利用相似比计算出AB的长即可.
解:∵AB⊥BC,CD⊥BC,
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:30=120:40,
∴AB=90,
即这条河的大致宽度是90m.
故选:A.
12.【答案】D
【解析】分别利用相似三角形的判定方法判断得出即可.
解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
C、当=时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
D、无法得到△ABP∽△ACB,故此选项符合题意.
故选:D.
13.【答案】
【解析】根据平行线分线段成比例定理得到,即,由此即可得到答案.
解:∵,
∴,即,
∴,
故答案为:.
【点睛】本题主要考查了平行线分线段成比例定理,熟知平行线分线段成比例定理是解题的关键.
14.【答案】6
【解析】利用平行线分线段长比例定理得到==1,即AF=FD,所以EF为△ADC的中位线,则EF=CD=BD,再利用EF∥BD得到==,所以DG=2FG=2,然后计算FD,从而得到AD的长.
解:∵△ABC的两条中线AD,BE交于点G,
∴BD=CD,AE=CE,
∵EF∥CD,
∴==1,即AF=FD,
∴EF为△ADC的中位线,
∴EF=CD,
∴EF=BD,
∵EF∥BD,
∴==,
∴DG=2FG=2,
∴FD=2+1=3,
∴AD=2FG=6.
故答案为6.
15.【答案】4:9
【解析】根据相似三角形周长的比等于相似比求出相似比,再根据相似三角形面积的比等于相似比的平方求解即可.
解:∵两个相似三角形的周长比为2:3,
∴这两个相似三角形的相似比为2:3,
∴它们的面积比是4:9.
故答案为:4:9.
16.【答案】+1或3+
【解析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.
解:根据黄金分割点的概念,应有两种情况,
当AB是较短线段时,AB=2÷=+1;
当AB是较长线段时,则AB=2+(+1)=3+.
故答案为:+1或3+.
17.【答案】3
【解析】由三角形中位线定理得到DF=BC;然后根据直角三角形斜边上的中线等于斜边的一半得到AE=BC,则DF=AE.
解:如图,∵在直角△ABC中,∠BAC=90°,D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC.
又∵点E是直角△ABC斜边BC的中点,
∴AE=BC,
∵DF=3,
∴DF=AE.
故填:3.
18.【答案】∠AED=∠B
【解析】要使两三角形相似,已知有一组公共角,则可以再添加一组角相等来判定其相似.
解:∠AED=∠B.
19.【解析】根据两边成比例且夹角相等的两个三角形相似可得结论.
证明:∵AD=1,AB=3,AC=,
∴,,
∴,
又∵∠A=∠A,
∴△ACD∽△ABC.
20.【解析】根据相似三角形的判定即可求出答案.
解:∵∠1=∠2,∠DPA=∠CPB,
∴△ADP∽△BCP,
∴=2,
∵AD=3,
∴BC=1.5.
21.【解析】根据DE∥BC,EF∥AB,得到四边形DBFE是平行四边形,根据平行四边形的性质得到DE=BF,由DE∥BC,推出三角形相似,于是得到=,即可得到结论.
解:∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∴DE=BF,
∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∴=.
22.【解析】利用三角形外角的性质及∠DEC=∠ADB可得出∠ADE=∠C,结合∠DAE=∠CAD即可证出△AED∽△ADC解决问题.
证明:∵∠DEC=∠DAE+∠ADE,∠ADB=∠DAE+∠C,∠DEC=∠ADB,
∴∠ADE=∠C.
又∵∠DAE=∠CAD,
∴△AED∽△ADC.
∴=,
∴AD2=AC AE,
∵AD=AB,
∴AB2=AC AE.
23.【解析】由平行的性质结合条件可得到∠AFB=∠EDA和∠BAE=∠AED,可证得结论.
证明:∵四边形ABCD是平行四边形,
∴∠BAF=∠AED,且∠C+∠D=180°,
又∵∠BFE+∠BFA=180°,
∵∠BFE=∠C,
∴∠BFA=∠D,
∴△ABF∽△EAD.
24.【解析】连接BD,取BD的中点H,连接HE,HF,根据三角形的中位线的性质得到FH∥BM,FH=AB,EH∥CN,EH=CD,根据平行线的性质得到∠BME=∠HFE,∠CNE=∠HEF,根据等腰三角形的性质得到∠HFE=∠HEF,等量代换即可得到结论.
证明:连接BD,取BD的中点H,连接HE,HF,
∵E、F分别是BC、AD的中点,
∴FH∥BM,FH=AB,EH∥CN,EH=CD,
∴∠BME=∠HFE,∠CNE=∠HEF,
∵AB=CD,
∴FH=EH,
∴∠HFE=∠HEF,
∴∠BME=∠CNE.
25.【解析】要使两个三角形相似,则可能是△APD∽△BPC,也可能是△APD∽△BCP,所以应分两种情况讨论,进而求解AP的值即可.
解:可设PA的长为x,
当△APD∽△BCP时,则=,即=,解得x=1或x=6.
假设△APD∽△BPC,则=,即=,
解得x=;
综上所述,AP的长度为1、6或.
26.【答案】(1)证明见详解
(2)
(3)
【解析】(1)利用,证明,利用相似比即可证明此问;
(2)由(1)得,,得出是等腰三角形,利用三角形相似即可求出值;
(3)遵循第(1)、(2)小问的思路,延长交于点M,连接,作,垂足为N.构造出等腰三角形、含30°、45°角的特殊直角三角形,求出、的值,即可得出的长.
【小问1详解】
解:∵,
∴,
∴,
∴.
∵,
∴.
【小问2详解】
解:由(1)得,
∵,
∴.
∵,
∴.
∵,
∴.
∴.
【小问3详解】
解:如图,延长交于点M,连接,作,垂足为N.
在中,.
∵,
∴由(1)得,
∵,
∴,
∴.
∵,
∴,
∴.
∵平分,
∴,
∴.
∴.在中,.
∵,
∴,
∴.
【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识,遵循构第(1)、(2)小问的思路,构造出等腰三角形和特殊的直角三角形是解决本题的关键.
第23章图形的相似
一、选择题(共12题;每小题4分,共48分)
1.若,则的值为( )
A. B. C. D.
2.)已知,且a+b+c≠0,则k的值是( )
A. 2 B. 3 C. D.
3.如图,△ABC与△DEF位似,点O是它们的位似中心,且相似比为1:2,则△ABC与△DEF的周长之比是( )
A. 1:2 B. 1:4
C. 1:3 D. 1:9
4.如图,已知矩形ABCD,AD=24,CD=16,点R、P分别是DC,BC上的点,点E、F分别是AP,RP的中点,当点P在BC上从B向C移动,而点R不动时,若CR=9,则EF=( )
A. 12 B. 12.5
C. 9 D. 不能确定
5.如图,直线a∥b∥c,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB:BC=1:2,DE=3,则EF的长为( )
A. 1.5 B. 6 C. 9 D. 12
6.如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则AD=( )
A. 2 B. 1
C. D.
7.如图,D、E分别是△ABC边AB、AC上的点,DE∥BC,且S△ADE:S四边形DBCE=1:8,那么AD:BD的值为( )
A. 1:9 B. 1:3 C. 1:8 D. 1:2
8.比例尺为1:1000000的地图上,A、B两地间的图上距离为2厘米,则两地间的实际距离是( )千米.
A. 0.2 B. 2 C. 20 D. 200
9.如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是( )
A. 5m B. 10m C. 20m D. 40m
10.如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
A. 3.5 B. 4 C. 7 D. 14
11.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )
A. 90m B. 60m C. 100m D. 120m
12.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A. ∠ABP=∠C B. ∠APB=∠ABC
C. = D. =
二、填空题(共6题;每小题4分,共24分)
13.如图,已知直线,且,,则________.
14.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=1,则AD=_____.
15.若两个相似三角形的周长比为2:3,则它们的面积比是_____.
16.若点C是线段AB的黄金分割点,且AC=2,则AB=_____.
17.直角△ABC中,∠BAC=90°,D、E、F分别为AB、BC、AC的中点,已知DF=3,则AE=_____.
18.如图,D,E分别是△ABC的边AB,AC上的点,请你添加一个条件,使△ABC与△AED相似,你添加的条件是_____.
三、解答题(共8题;共78分)
19.(8分)如图,在△ABC中,点D是AB上一点,且AD=1,AB=3,.
求证:△ACD∽△ABC.
20.(8分)如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,AD=3,DP=2,CP=1,求BC的长.
21.(10分)如图,点D,E,F分别在△ABC的边AB,AC,BC上,且DE∥BC,EF∥AB.求证:=.
22.(10分)如图,在△ABC中,点D在BC边上,AD=AB,点E在AC边上,且∠DEC=∠ADB.求证:AB2=AE AC.
23.(10分)如图,在平行四边形ABCD中,E为DC上一点,连接AE,F为AE上一点,且∠BFE=∠C.求证:△ABF∽△EAD.
24.(10分)如图,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.
25.(10分)直角梯形ABCD中,∠A=∠B=90°,AB=7,AD=2,BC=3,在AB上取一点P,使△APD与△BPC相似,求AP的长.
26.(12分)
(1)如图1,在中,D,E,F分别为上的点,交于点G,求证:.
(2)如图2,在(1)的条件下,连接.若,求的值.
(3)如图3,在中,与交于点O,E为上一点,交于点G,交于点F.若平分,求的长.
试卷答案
1.【答案】A
【解析】根据,可得a=,代入代数式求解即可.
解:∵,
∴a=,
∴==,
故选:A.
2.【答案】D
【解析】根据比例的基本性质,即可进行解答.
解:∵,a+b+c≠0,
∴,整理得:,
∴.
故选:D.
3.【答案】A
【解析】根据两三角形位似,周长比等于相似比即可求解.
解:∵△ABC与△DEF位似,点O是它们的位似中心,且相似比为1:2,
∴△ABC与△DEF的周长之比是1:2,
故选:A.
4.【答案】B
【解析】连接AR,根据勾股定理可求出AR,再根据中位线定理即可得出答案.
解:如图,连接AR,
∵CR=9,CD=16,
∴DR=7,
∵AD=24,∠D=90°,
∴AR==25,
∵点E、F分别是AP,RP的中点,
∴EF=AR=12.5,
故选:B.
5.【答案】B
【解析】由a∥b∥c,可得,由此即可解决问题.
解:∵a∥b∥c,
∴,
∴,
∴EF=6,
故选:B.
6.【答案】B
【解析】由∠DBC=∠A,BC=,AC=3可证明△CBD∽△CAB,由此可得,代入可求得CD,即可得到AD.
解:∵∠DBC=∠A,∠C=∠C,
∴△CBD∽△CAB,
∴,即,
∴CD=2,
∴AD=AC-CD=3-2=1.
故选:B.
7.【答案】D
【解析】证明△ADE∽△ABC,由S△ADE:S四边形DBCE=1:8,得S△ADE:S△ABC=1:9,根据相似三角形面积的比等于相似比的平方可得出答案.
解:∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=AD2:AB2,
∵S△ADE:S四边形DBCE=1:8,
∴S△ADE:S△ABC=1:9,
∴AD:AB=1:3,
∴AD:BD=1:2.
故选:D.
8.【答案】C
【解析】根据实际距离=图上距离÷比例尺.代值计算即可得出答案.
解:根据题意得:
2÷=2000000(厘米),
2000000厘米=20千米.
故选:C.
9.【答案】C
【解析】根据三角形中位线定理解答即可.
解:∵点C,D分别是OA,OB的中点,
∴AB=2CD=20(m),
故选:C.
10.【答案】A
【解析】由菱形的周长可求得AB的长,再利用三角形中位线定理可求得答案0
解:
∵四边形ABCD为菱形,
∴AB=×28=7,且O为BD的中点,
∵E为AD的中点,
∴OE为△ABD的中位线,
∴OE=AB=3.5,
故选:A.
11.【答案】A
【解析】先证明△ABD∽△ECD,然后利用相似比计算出AB的长即可.
解:∵AB⊥BC,CD⊥BC,
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:30=120:40,
∴AB=90,
即这条河的大致宽度是90m.
故选:A.
12.【答案】D
【解析】分别利用相似三角形的判定方法判断得出即可.
解:A、当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
B、当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
C、当=时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项不符合题意;
D、无法得到△ABP∽△ACB,故此选项符合题意.
故选:D.
13.【答案】
【解析】根据平行线分线段成比例定理得到,即,由此即可得到答案.
解:∵,
∴,即,
∴,
故答案为:.
【点睛】本题主要考查了平行线分线段成比例定理,熟知平行线分线段成比例定理是解题的关键.
14.【答案】6
【解析】利用平行线分线段长比例定理得到==1,即AF=FD,所以EF为△ADC的中位线,则EF=CD=BD,再利用EF∥BD得到==,所以DG=2FG=2,然后计算FD,从而得到AD的长.
解:∵△ABC的两条中线AD,BE交于点G,
∴BD=CD,AE=CE,
∵EF∥CD,
∴==1,即AF=FD,
∴EF为△ADC的中位线,
∴EF=CD,
∴EF=BD,
∵EF∥BD,
∴==,
∴DG=2FG=2,
∴FD=2+1=3,
∴AD=2FG=6.
故答案为6.
15.【答案】4:9
【解析】根据相似三角形周长的比等于相似比求出相似比,再根据相似三角形面积的比等于相似比的平方求解即可.
解:∵两个相似三角形的周长比为2:3,
∴这两个相似三角形的相似比为2:3,
∴它们的面积比是4:9.
故答案为:4:9.
16.【答案】+1或3+
【解析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.
解:根据黄金分割点的概念,应有两种情况,
当AB是较短线段时,AB=2÷=+1;
当AB是较长线段时,则AB=2+(+1)=3+.
故答案为:+1或3+.
17.【答案】3
【解析】由三角形中位线定理得到DF=BC;然后根据直角三角形斜边上的中线等于斜边的一半得到AE=BC,则DF=AE.
解:如图,∵在直角△ABC中,∠BAC=90°,D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC.
又∵点E是直角△ABC斜边BC的中点,
∴AE=BC,
∵DF=3,
∴DF=AE.
故填:3.
18.【答案】∠AED=∠B
【解析】要使两三角形相似,已知有一组公共角,则可以再添加一组角相等来判定其相似.
解:∠AED=∠B.
19.【解析】根据两边成比例且夹角相等的两个三角形相似可得结论.
证明:∵AD=1,AB=3,AC=,
∴,,
∴,
又∵∠A=∠A,
∴△ACD∽△ABC.
20.【解析】根据相似三角形的判定即可求出答案.
解:∵∠1=∠2,∠DPA=∠CPB,
∴△ADP∽△BCP,
∴=2,
∵AD=3,
∴BC=1.5.
21.【解析】根据DE∥BC,EF∥AB,得到四边形DBFE是平行四边形,根据平行四边形的性质得到DE=BF,由DE∥BC,推出三角形相似,于是得到=,即可得到结论.
解:∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∴DE=BF,
∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∴=.
22.【解析】利用三角形外角的性质及∠DEC=∠ADB可得出∠ADE=∠C,结合∠DAE=∠CAD即可证出△AED∽△ADC解决问题.
证明:∵∠DEC=∠DAE+∠ADE,∠ADB=∠DAE+∠C,∠DEC=∠ADB,
∴∠ADE=∠C.
又∵∠DAE=∠CAD,
∴△AED∽△ADC.
∴=,
∴AD2=AC AE,
∵AD=AB,
∴AB2=AC AE.
23.【解析】由平行的性质结合条件可得到∠AFB=∠EDA和∠BAE=∠AED,可证得结论.
证明:∵四边形ABCD是平行四边形,
∴∠BAF=∠AED,且∠C+∠D=180°,
又∵∠BFE+∠BFA=180°,
∵∠BFE=∠C,
∴∠BFA=∠D,
∴△ABF∽△EAD.
24.【解析】连接BD,取BD的中点H,连接HE,HF,根据三角形的中位线的性质得到FH∥BM,FH=AB,EH∥CN,EH=CD,根据平行线的性质得到∠BME=∠HFE,∠CNE=∠HEF,根据等腰三角形的性质得到∠HFE=∠HEF,等量代换即可得到结论.
证明:连接BD,取BD的中点H,连接HE,HF,
∵E、F分别是BC、AD的中点,
∴FH∥BM,FH=AB,EH∥CN,EH=CD,
∴∠BME=∠HFE,∠CNE=∠HEF,
∵AB=CD,
∴FH=EH,
∴∠HFE=∠HEF,
∴∠BME=∠CNE.
25.【解析】要使两个三角形相似,则可能是△APD∽△BPC,也可能是△APD∽△BCP,所以应分两种情况讨论,进而求解AP的值即可.
解:可设PA的长为x,
当△APD∽△BCP时,则=,即=,解得x=1或x=6.
假设△APD∽△BPC,则=,即=,
解得x=;
综上所述,AP的长度为1、6或.
26.【答案】(1)证明见详解
(2)
(3)
【解析】(1)利用,证明,利用相似比即可证明此问;
(2)由(1)得,,得出是等腰三角形,利用三角形相似即可求出值;
(3)遵循第(1)、(2)小问的思路,延长交于点M,连接,作,垂足为N.构造出等腰三角形、含30°、45°角的特殊直角三角形,求出、的值,即可得出的长.
【小问1详解】
解:∵,
∴,
∴,
∴.
∵,
∴.
【小问2详解】
解:由(1)得,
∵,
∴.
∵,
∴.
∵,
∴.
∴.
【小问3详解】
解:如图,延长交于点M,连接,作,垂足为N.
在中,.
∵,
∴由(1)得,
∵,
∴,
∴.
∵,
∴,
∴.
∵平分,
∴,
∴.
∴.在中,.
∵,
∴,
∴.
【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识,遵循构第(1)、(2)小问的思路,构造出等腰三角形和特殊的直角三角形是解决本题的关键.
