6.1平方根(3)课件
图片预览







文档简介
课件25张PPT。6.1 平方根(第3课时)如果一个数的平方等于9,这个数是多少?1.归纳平方根的概念由于 ,
所以这个数是3或-3.根据上面的研究过程填表:1.归纳平方根的概念如果我们把 分别叫做
的平方根,你能类比算术
平方根的概念,给出平方根的概念吗?一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 ,那么x 叫做a的平方根.1.归纳平方根的概念例如:3和-3是 9的平方根,
简记 是9的平方根.如果一个数X的平方等于a,即 X2 = a,
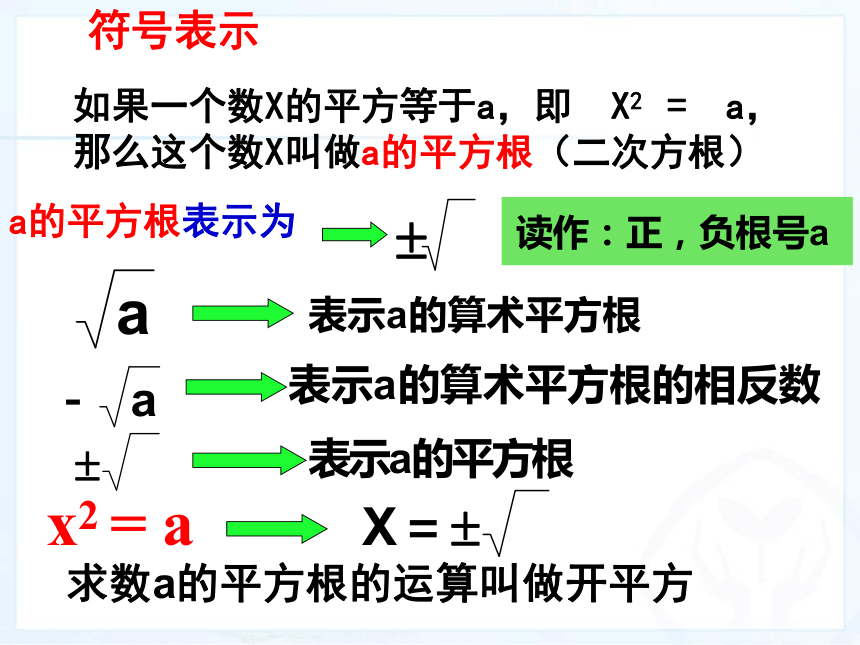
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a符号表示求数a的平方根的运算叫做开平方 填空:求平方求平方根
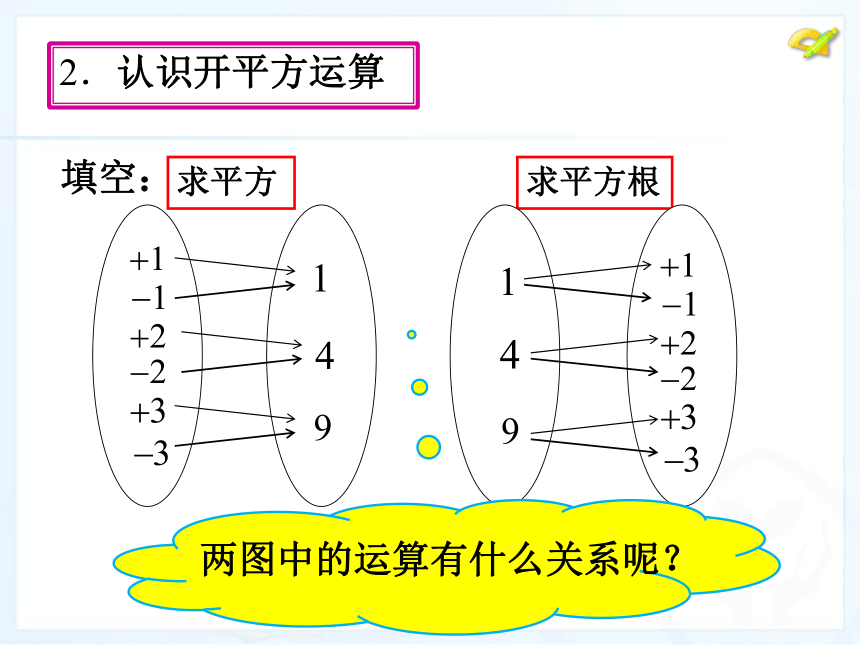
2.认识开平方运算求一个数的平方根的运算,叫做开平方。±3的平方等于9, 9的平方根是±3,
所以平方与开平方互为逆运算.初中所学的六种运算:
加法、减法、乘法、除法、乘方、开方.
对应的运算结果分别为:
和、 差、 积、 商、 幂、 方根.例1 求下列各数的平方根:3.例题解析 解:(1)因为 ,
所以100的平方根是 10 .
即 .例1 求下列各数的平方根:3.例题解析 解:(2)因为 ,
所以 的平方根是 .
即 . 例1 求下列各数的平方根:3.例题解析 解:(3)因为 ,
所以0.25的平方根是 .
即 .例1 求下列各数的平方根:3.例题解析 解:(4)因为 ,
所以 的平方根是 .
即 . 例1 求下列各数的平方根:3.例题解析 解:(5)因为 ,
所以0的平方根是0.
即 .
例2 判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是 ;
(5)-16的平方根是-4.3.例题解析正数的平方根有什么特点? 0的平方根是多少? 负数有平方根吗?4.归纳数的平方根的特征1.平方根包括算术平方根,算术平方根是平方根中非负的那一个.
2.存在条件相同.只有非负数才有平方根和算术平方根.
3.0的平方根和算术平方根均为0正数a的算术平方根有一个
正数a的平方根有两个
如果一个正数x的平方等于a,那么这个正数就叫做a的算术平方根
如果一个数的平方等于a,这个数就叫做a的平方根
符号不同个数不同定义不同用 表示
用 表示平方根与算术平方根的比较例3 判断下列各式计算是否正确,并说明理由.5.例题解析例4 说出下列各式的意义,并求它们的值:5.例题解析解:(1) ; (2) ; (3) .1、如果一个正数的一个平方根为4,则另一个平
方根为多少?,:解:因为一个正数的平方根有两个,它
们互为相反数,所以另一个平方根为-4练习2、如果一个正数的两个平方根为和,请你求出这个正数
(1)3、求下列各式中的x解:由题意,得 (a+1)+(2a-7)=0
解得: a=2
也可求出2a-7,
再求它的平方=注意:是求平方根4) 的平方根是 ± 4 ( )1) 1.21 的平方根是 ± 1.1 ( )2) 9 的平方根是 3 ( ) 3) -5 是 25 的平方根 ( ) 5) 平方根是本身的数有0 ,1 ( ) √ ×× ×√课堂检测
6)一个数的平方等于它本身,这个数 是 ;7)一个数的算术平方根等于它本身,这个数是 ;8)一个数的平方根等于它本身,这个数是 。0、10、10
(9)若a+1没有平方根,那么a的范围是 。
(10)若4a+1的平方根是±5,则a= 。(11)一个正数x的平方根等于m+1和m-3,
则m= ,x= 。a﹤-1614补充练习;±2-13256≥0-5互为相反数请谈谈你这节课的收获a的平方根底数幂被开方数 互为
逆运算根号2指数根指数教科书 习题6.1第3、4、7、8题8.布置作业
所以这个数是3或-3.根据上面的研究过程填表:1.归纳平方根的概念如果我们把 分别叫做
的平方根,你能类比算术
平方根的概念,给出平方根的概念吗?一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果 ,那么x 叫做a的平方根.1.归纳平方根的概念例如:3和-3是 9的平方根,
简记 是9的平方根.如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a符号表示求数a的平方根的运算叫做开平方 填空:求平方求平方根
2.认识开平方运算求一个数的平方根的运算,叫做开平方。±3的平方等于9, 9的平方根是±3,
所以平方与开平方互为逆运算.初中所学的六种运算:
加法、减法、乘法、除法、乘方、开方.
对应的运算结果分别为:
和、 差、 积、 商、 幂、 方根.例1 求下列各数的平方根:3.例题解析 解:(1)因为 ,
所以100的平方根是 10 .
即 .例1 求下列各数的平方根:3.例题解析 解:(2)因为 ,
所以 的平方根是 .
即 . 例1 求下列各数的平方根:3.例题解析 解:(3)因为 ,
所以0.25的平方根是 .
即 .例1 求下列各数的平方根:3.例题解析 解:(4)因为 ,
所以 的平方根是 .
即 . 例1 求下列各数的平方根:3.例题解析 解:(5)因为 ,
所以0的平方根是0.
即 .
例2 判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是 ;
(5)-16的平方根是-4.3.例题解析正数的平方根有什么特点? 0的平方根是多少? 负数有平方根吗?4.归纳数的平方根的特征1.平方根包括算术平方根,算术平方根是平方根中非负的那一个.
2.存在条件相同.只有非负数才有平方根和算术平方根.
3.0的平方根和算术平方根均为0正数a的算术平方根有一个
正数a的平方根有两个
如果一个正数x的平方等于a,那么这个正数就叫做a的算术平方根
如果一个数的平方等于a,这个数就叫做a的平方根
符号不同个数不同定义不同用 表示
用 表示平方根与算术平方根的比较例3 判断下列各式计算是否正确,并说明理由.5.例题解析例4 说出下列各式的意义,并求它们的值:5.例题解析解:(1) ; (2) ; (3) .1、如果一个正数的一个平方根为4,则另一个平
方根为多少?,:解:因为一个正数的平方根有两个,它
们互为相反数,所以另一个平方根为-4练习2、如果一个正数的两个平方根为和,请你求出这个正数
(1)3、求下列各式中的x解:由题意,得 (a+1)+(2a-7)=0
解得: a=2
也可求出2a-7,
再求它的平方=注意:是求平方根4) 的平方根是 ± 4 ( )1) 1.21 的平方根是 ± 1.1 ( )2) 9 的平方根是 3 ( ) 3) -5 是 25 的平方根 ( ) 5) 平方根是本身的数有0 ,1 ( ) √ ×× ×√课堂检测
6)一个数的平方等于它本身,这个数 是 ;7)一个数的算术平方根等于它本身,这个数是 ;8)一个数的平方根等于它本身,这个数是 。0、10、10
(9)若a+1没有平方根,那么a的范围是 。
(10)若4a+1的平方根是±5,则a= 。(11)一个正数x的平方根等于m+1和m-3,
则m= ,x= 。a﹤-1614补充练习;±2-13256≥0-5互为相反数请谈谈你这节课的收获a的平方根底数幂被开方数 互为
逆运算根号2指数根指数教科书 习题6.1第3、4、7、8题8.布置作业
