5.2.1平行线课件
图片预览




文档简介
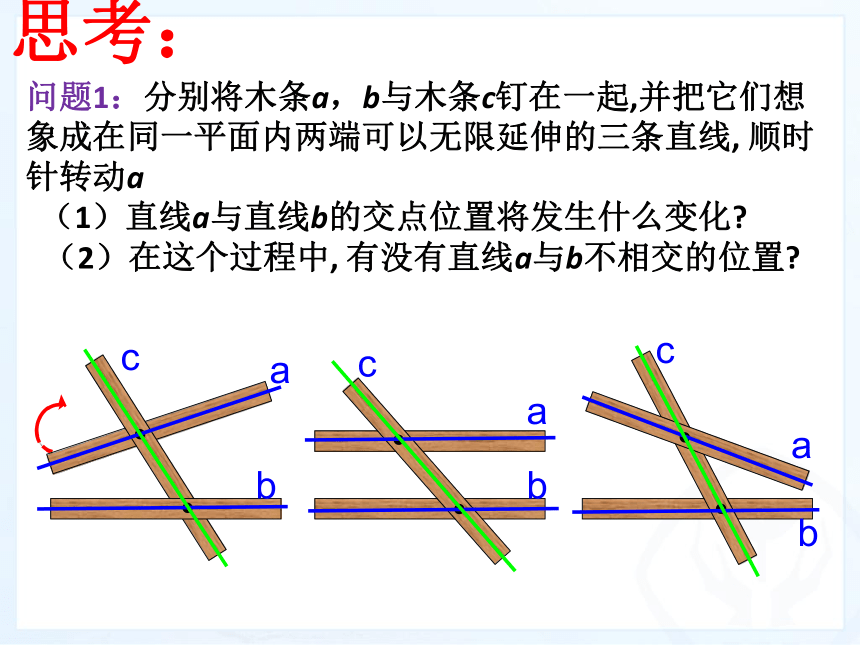
课件19张PPT。5.2.1 平行线问题1:分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线, 顺时针转动a
(1)直线a与直线b的交点位置将发生什么变化?
(2)在这个过程中, 有没有直线a与b不相交的位置?
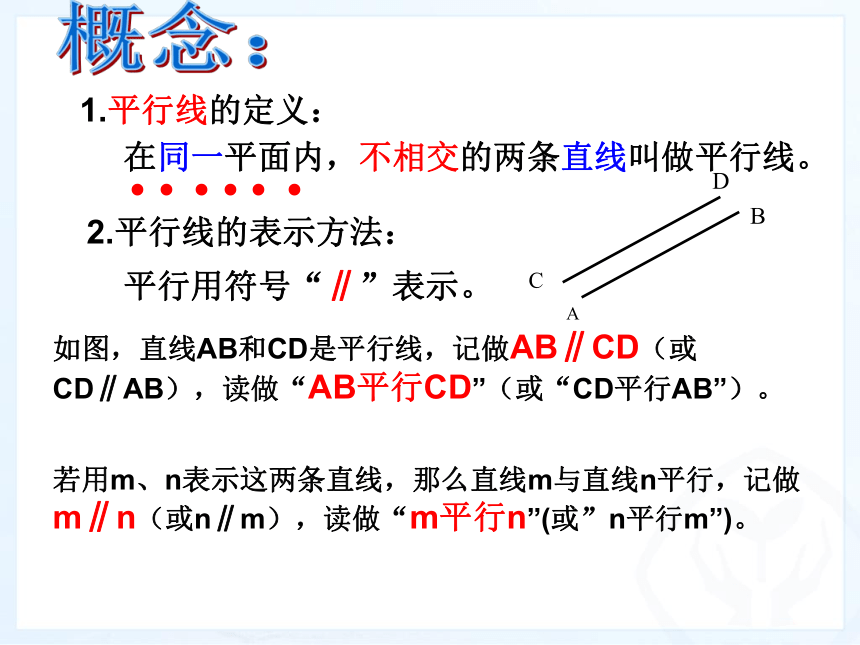
思考:平行线概念:同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之, 同一平面内, 不相交的两条直线叫做平行线.直线a与b是平行线, 记作a∥b.概念:1.平行线的定义:在同一平面内,不相交的两条直线叫做平行线。2.平行线的表示方法:平行用符号“∥”表示。如图,直线AB和CD是平行线,记做AB∥CD(或CD∥AB),读做“AB平行CD”(或“CD平行AB”)。若用m、n表示这两条直线,那么直线m与直线n平行,记做m∥n(或n∥m),读做“m平行n”(或”n平行m”)。平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件,
(2)“不相交”就是说两条直线没有
交点,
(3)平行线指的是“两条直线”而不
是两条射线或两条线段.注意:讨论与探究1、平行线要求在同一平面内,那么在同一平面内两直线
的位置关系一共有几种呢?(小组先讨论再实践)结论:在同一平面内,两直线的位置关系有
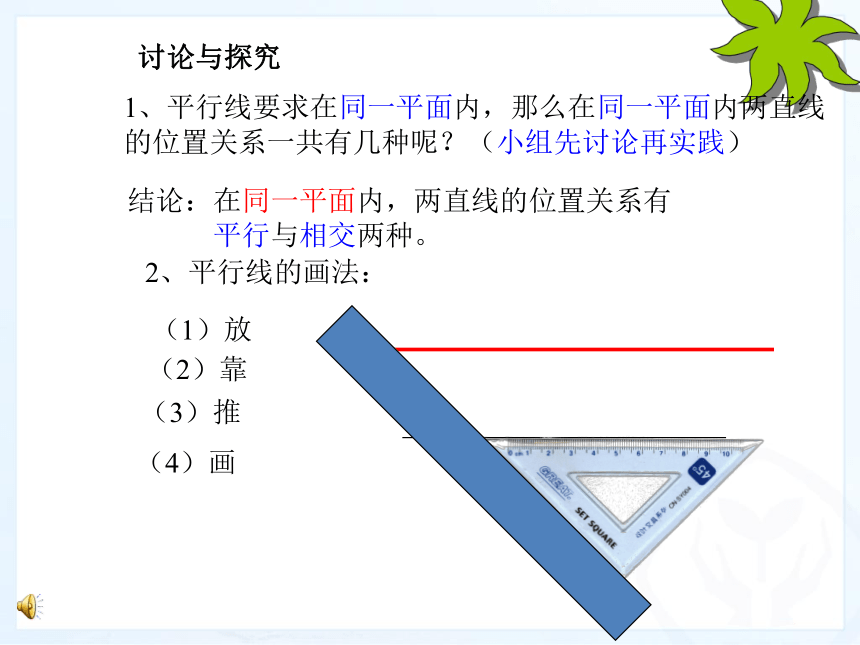
平行与相交两种。2、平行线的画法:(1)放(2)靠(3)推(4)画●一放二靠三推四画 已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。PBA一、放二、靠三、推四、画●PBA动手实践 过直线AB外一点P作直线AB的平行线,
看看你能作出吗?能作出几条?结论:经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据. (1)经过点A画出直线n的平行线,能画几条? (2)过点B画一条直线与直线n平行,它与(1)中所画的直线平行吗? 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。··ABn平行线的传递性 (平行公理的推论):结论:ma探究新知如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于P因为AB//EF,CD//EF
于是过点P就有两条直线AB,CD都与EF平行。
根据平行公理,这是不可能的
也就是说,AB与CD不能相交,只能平行。平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行几何语言表达: a//c , c//b(已知)
? a//b(平行公理的推论)?由此可见:平行具有传递性平行公理:经过直线外一点,有且只有一条直线与这条直线平行.平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.如果b∥a,c∥a,那么b∥c. 练习:读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.(1)(2).PEFDC温故而知新1、下列说法正确的个数是( )(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行A、0 B、1 C、2 D、4 B2、下列推理正确的是( )A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。C3、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
在同一直线上经过直线外一点,有且只有一条直线与这条直线平行ABEF如果两条直线都和第三条直线平行,
那么这两条直线也互相平行 1.同一平面内,三条直线的交点可以有 个. 2.对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是什么位置关系?相交练习0或1或2或3 本节课你的收获是什么?小结(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理(6)平行线公理的推论。(五)布置作业教科书第12页练习
(1)直线a与直线b的交点位置将发生什么变化?
(2)在这个过程中, 有没有直线a与b不相交的位置?
思考:平行线概念:同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.换言之, 同一平面内, 不相交的两条直线叫做平行线.直线a与b是平行线, 记作a∥b.概念:1.平行线的定义:在同一平面内,不相交的两条直线叫做平行线。2.平行线的表示方法:平行用符号“∥”表示。如图,直线AB和CD是平行线,记做AB∥CD(或CD∥AB),读做“AB平行CD”(或“CD平行AB”)。若用m、n表示这两条直线,那么直线m与直线n平行,记做m∥n(或n∥m),读做“m平行n”(或”n平行m”)。平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件,
(2)“不相交”就是说两条直线没有
交点,
(3)平行线指的是“两条直线”而不
是两条射线或两条线段.注意:讨论与探究1、平行线要求在同一平面内,那么在同一平面内两直线
的位置关系一共有几种呢?(小组先讨论再实践)结论:在同一平面内,两直线的位置关系有
平行与相交两种。2、平行线的画法:(1)放(2)靠(3)推(4)画●一放二靠三推四画 已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。PBA一、放二、靠三、推四、画●PBA动手实践 过直线AB外一点P作直线AB的平行线,
看看你能作出吗?能作出几条?结论:经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据. (1)经过点A画出直线n的平行线,能画几条? (2)过点B画一条直线与直线n平行,它与(1)中所画的直线平行吗? 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。··ABn平行线的传递性 (平行公理的推论):结论:ma探究新知如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于P因为AB//EF,CD//EF
于是过点P就有两条直线AB,CD都与EF平行。
根据平行公理,这是不可能的
也就是说,AB与CD不能相交,只能平行。平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行几何语言表达: a//c , c//b(已知)
? a//b(平行公理的推论)?由此可见:平行具有传递性平行公理:经过直线外一点,有且只有一条直线与这条直线平行.平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.如果b∥a,c∥a,那么b∥c. 练习:读下列语句,并画出图形.
(1)如图(1),过点A画EF ∥ BC;
(2)如图(2),在∠AOB内取一点P,过点P画PC ∥ OA交OB于C,PD ∥ OB交OA于D.(1)(2).PEFDC温故而知新1、下列说法正确的个数是( )(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行A、0 B、1 C、2 D、4 B2、下列推理正确的是( )A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。C3、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
在同一直线上经过直线外一点,有且只有一条直线与这条直线平行ABEF如果两条直线都和第三条直线平行,
那么这两条直线也互相平行 1.同一平面内,三条直线的交点可以有 个. 2.对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是什么位置关系?相交练习0或1或2或3 本节课你的收获是什么?小结(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理(6)平行线公理的推论。(五)布置作业教科书第12页练习
