5.2.2平行线的判定课件
文档属性
| 名称 | 5.2.2平行线的判定课件 |  | |
| 格式 | zip | ||
| 文件大小 | 695.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-01 12:44:59 | ||
图片预览



文档简介
课件20张PPT。5.2.2 平行线的判定
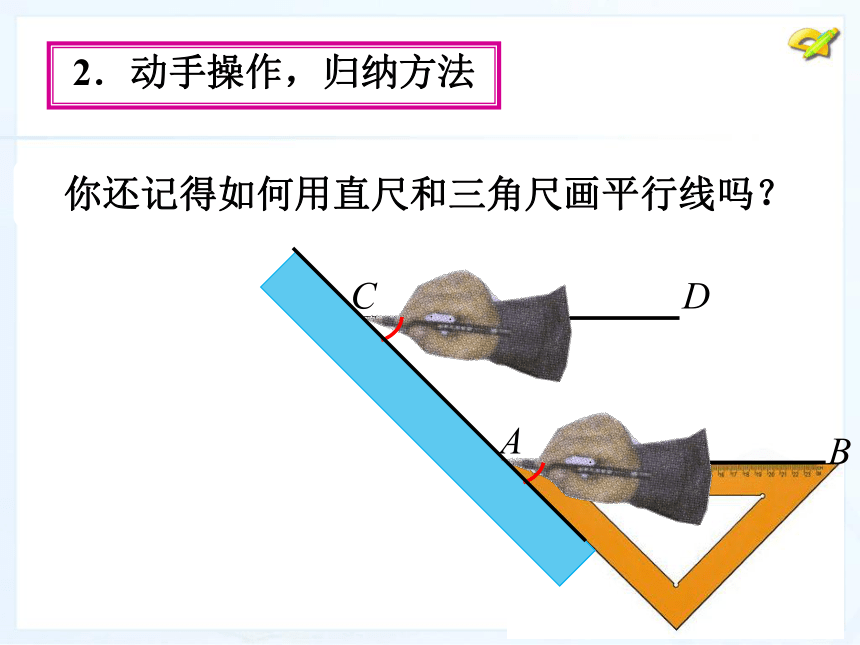
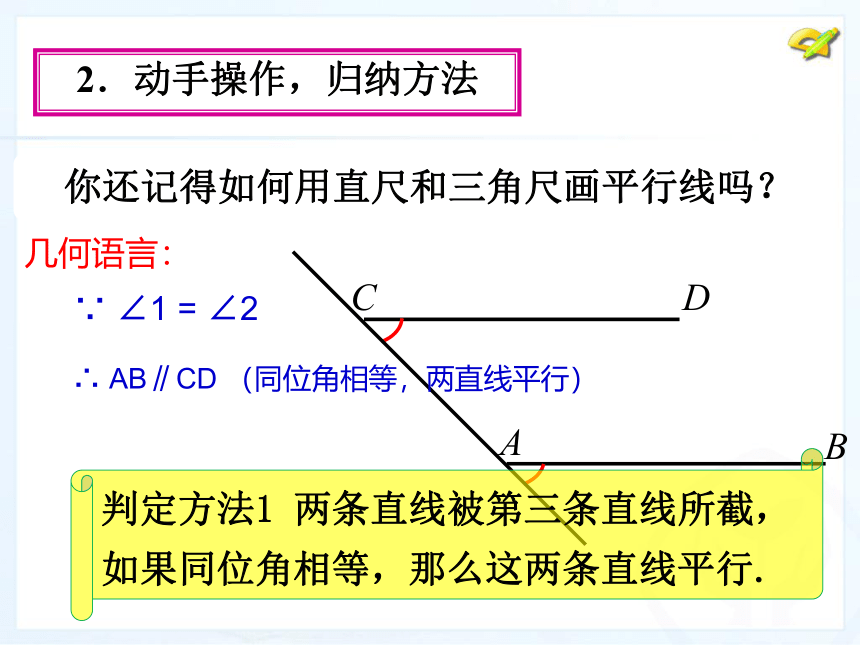
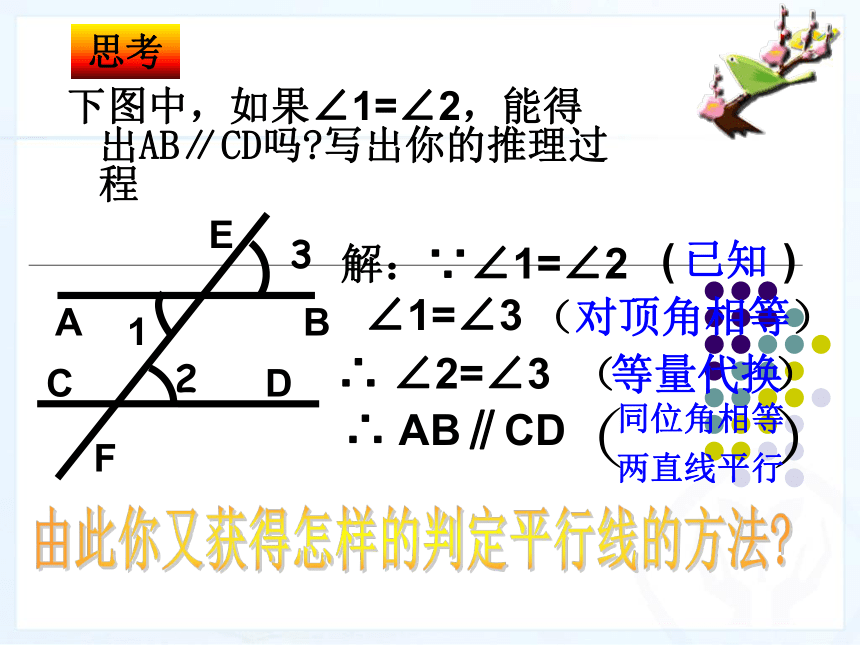
(第1课时)(1) 根据定义. (2) 根据平行公理的推论.1.梳理旧知,引出新课 如何判断两条直线是否平行?2、平行线的画法:2. 动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:·ABCD2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.几何语言:∵ ∠1 = ∠2∴ AB∥CD (同位角相等,两直线平行)下图中,如果∠1=∠2,能得出AB∥CD吗?写出你的推理过程思考解:∵∠1=∠2
∠1=∠3
∴ ∠2=∠3∴ AB∥CDB1ACDF32E由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 ( )
同位角相等
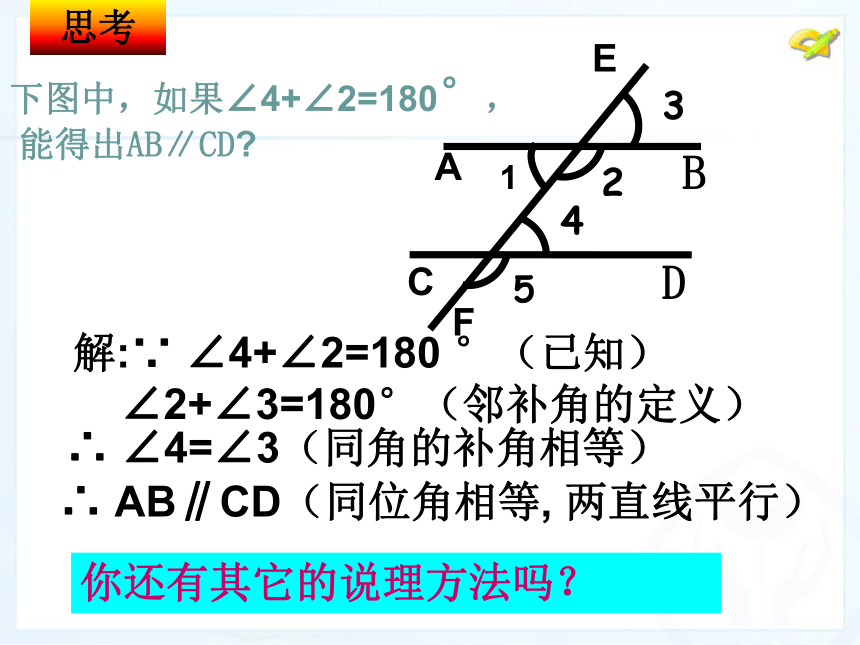
两直线平行 3.简单推理,得出判定方法2和判定方法3 如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.下图中,如果∠4+∠2=180°,
能得出AB∥CD?思考解:∵ ∠4+∠2=180 °(已知)
∠2+∠3=180°(邻补角的定义)
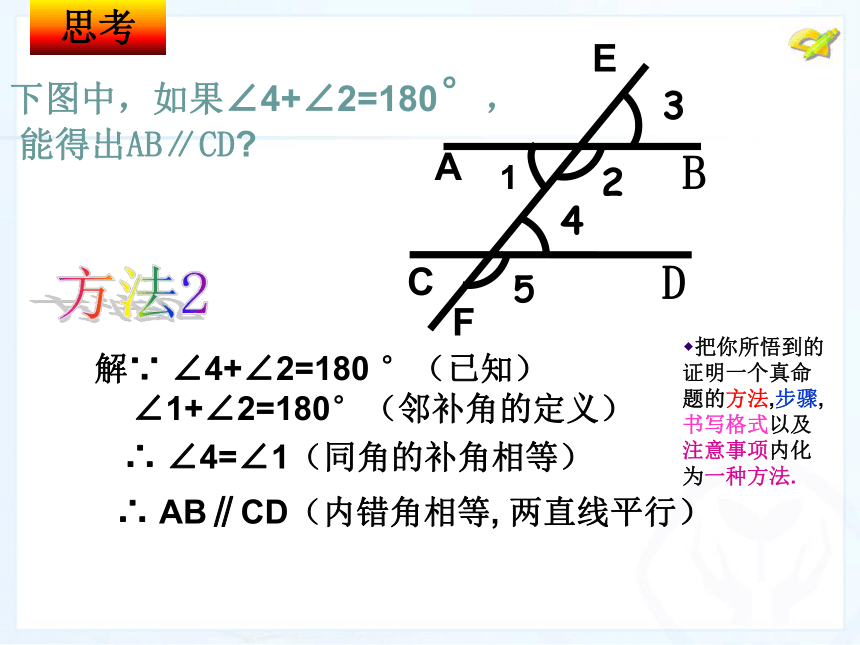
∴ ∠4=∠3(同角的补角相等)∴ AB∥CD(同位角相等, 两直线平行)1AC3245DBEF你还有其它的说理方法吗?下图中,如果∠4+∠2=180°,
能得出AB∥CD?思考1AC3245DBEF方法2解∵ ∠4+∠2=180 °(已知)
∠1+∠2=180°(邻补角的定义)∴ ∠4=∠1(同角的补角相等)∴ AB∥CD(内错角相等, 两直线平行)把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.3.简单推理,得出判定方法2和判定方法3 如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行. 平行线的判定同位角相等,两直线平行.4.巩固新知,深化理解例1 如图,你能说出木工用图中的角尺画平行线的道理吗?(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AD∥BC .根据同位角相等,两直线平行.(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据内错角相等,两直线平行.(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据同旁内角互补,两直线平行.如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDCBAD21E 证明:∵∠1+∠A=180o3练习∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD(1)本节课,你学习了哪些平行线的判定方法?5.归纳小结(2)你能用自己的语言叙述得到平行线判定方法的过程吗?(3)判定方法2和判定方法3是通过简单推理得到的,在推理论证中需要注意哪些问题?平行线的判定?公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
5.平行线的定义.
判定两条直线是否平行的方法有: 教科书 习题5.2 第1、4、7题6.布置作业
∠1=∠3
∴ ∠2=∠3∴ AB∥CDB1ACDF32E由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 ( )
同位角相等
两直线平行 3.简单推理,得出判定方法2和判定方法3 如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.下图中,如果∠4+∠2=180°,
能得出AB∥CD?思考解:∵ ∠4+∠2=180 °(已知)
∠2+∠3=180°(邻补角的定义)
∴ ∠4=∠3(同角的补角相等)∴ AB∥CD(同位角相等, 两直线平行)1AC3245DBEF你还有其它的说理方法吗?下图中,如果∠4+∠2=180°,
能得出AB∥CD?思考1AC3245DBEF方法2解∵ ∠4+∠2=180 °(已知)
∠1+∠2=180°(邻补角的定义)∴ ∠4=∠1(同角的补角相等)∴ AB∥CD(内错角相等, 两直线平行)把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.3.简单推理,得出判定方法2和判定方法3 如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行. 平行线的判定同位角相等,两直线平行.4.巩固新知,深化理解例1 如图,你能说出木工用图中的角尺画平行线的道理吗?(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AD∥BC .根据同位角相等,两直线平行.(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据内错角相等,两直线平行.(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据同旁内角互补,两直线平行.如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDCBAD21E 证明:∵∠1+∠A=180o3练习∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD(1)本节课,你学习了哪些平行线的判定方法?5.归纳小结(2)你能用自己的语言叙述得到平行线判定方法的过程吗?(3)判定方法2和判定方法3是通过简单推理得到的,在推理论证中需要注意哪些问题?平行线的判定?公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
5.平行线的定义.
判定两条直线是否平行的方法有: 教科书 习题5.2 第1、4、7题6.布置作业
