人教版数学九年级上册24.1《 圆的有关性质》课件(共34张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1《 圆的有关性质》课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 21:09:26 | ||
图片预览









文档简介
(共34张PPT)
第二十四章 圆
24.1 圆的有关性质
圆
01
认识圆,理解圆的定义.
02
掌握弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念,并了解它们之间的区别联系.
教学目标
情景导入
圆是一种基本的几何图形,圆形物体在生活中随处可见。
情景导入
你还能举例说出生活中还有哪些“圆”吗?
古希腊的数学家毕达哥拉斯认为:“一切立体图形中最美的是球,一切平面图形中最美的是圆”。
新知探究
圆的定义
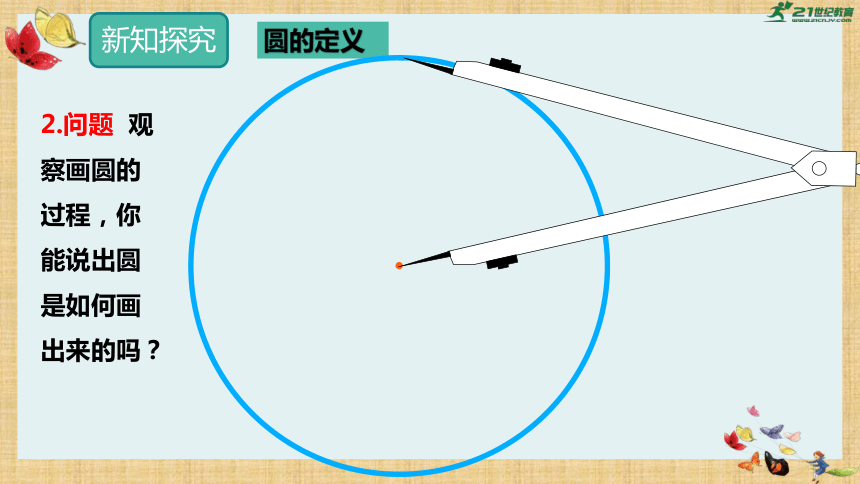
2.问题 观察画圆的过程,你能说出圆是如何画出来的吗?
B
B
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.
新知探究
圆的定义
圆的表示方法:在一个平面内,线段绕它固定的一个端点旋转一周,另一个端点所形成的图形叫做圆. 其固定的端点叫做圆心,线段叫做半径.
以点为圆心的圆,记作“⊙”,读作“圆”.
新知探究
圆的定义
新知探究
圆的定义
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
O
圆心相同,半径不同
半径相同,圆心不同
确定一个圆的要素
新知探究
圆的定义
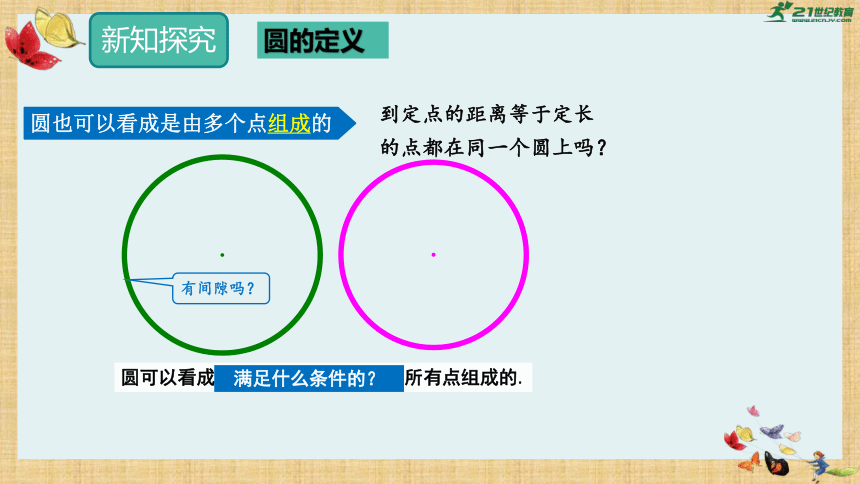
圆可以看成到定点距离等于定长的所有点组成的.
满足什么条件的?
有间隙吗?
圆也可以看成是由多个点组成的
到定点的距离等于定长
的点都在同一个圆上吗?
无数个圆
无数个圆
圆心、半径都确定
新知探究
圆的定义
2.如何画一个确定的圆?
想一想:1.以1cm为半径能画几个圆,以点O为圆心能画几个圆?
新知探究
圆的定义
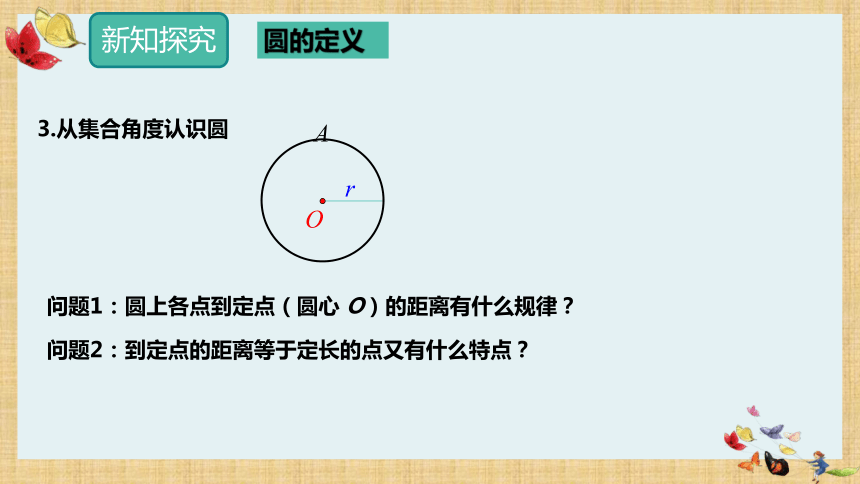
3.从集合角度认识圆
问题1:圆上各点到定点(圆心 O)的距离有什么规律?
问题2:到定点的距离等于定长的点又有什么特点?
·
r
O
A
新知探究
圆的定义
观察画圆过程
回答:
(1)圆上各点到定点 (圆心)的距离都等于 。
定长(半径r)
(2)到定点的距离等于定长的点都在 。
同一个圆上
圆的第二定义:
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形。
到定点的距离等于定长的点都在同一个圆上.
圆上各点到定点(圆心)的距离都等于定长(半径);
新知探究
圆的定义
动态:
总结归纳:圆的两种定义
圆心为、半径为的圆可以看成是所有到定点的距离等于定长的点的集合.
静态:
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载。它的意思是圆上各点到圆心的距离都等于半径。
小知识
新知探究
1、车轮为什么做成圆形的?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道路。
2、如果车轮做成椭圆或正方形的,坐车的人会是什么感觉?
巩固练习
如图,矩形ABCD的对角线AC、BD交于点O,求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
∴A、B、C、D在以O为圆心以OA为半径的圆上。矩形——四点共圆.
巩固练习
1、从树木的年轮,可以很清楚的看出树生长的年龄。如果一棵20年树龄的红杉树的树干直径是23cm,那么这棵红杉树的半径平均每年增加多少?
23÷20=1.15
1.15÷2=0.575
巩固练习
2、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺已不可。
周圆
位置
大小
新知探究
圆的有关概念
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
1.弦
新知探究
圆的有关概念
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
B
O
A
C
⌒
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
2.弧
新知探究
圆的有关概念
O
A
B
O
A
B
探索:圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
【发现】直径是最长的弦
新知探究
圆的有关概念
·
C
O
A
B
⌒
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
⌒
(如图中的AC)
(用三个字母表示,如图中的ACB)
3.优弧与劣弧
新知探究
圆的有关概念
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
新知探究
圆的有关概念
能够重合的两个圆是等圆。
半径相等的两个圆是等圆;
反过来说,同圆或等圆的半径相等。
4.等圆
新知探究
圆的有关概念
·
B
O1
A
在同圆或等圆中,能够互相重合的弧
·
D
O2
F
E
C
问题 长度相等的两段弧是等弧吗?为什么?
5.等弧
巩固练习
1.1.下列三个命题:①圆既是轴对称图形又是中心对称图形;②直径是弦;
③半径相等的两个半圆是等弧.其中正确的是( )
A.①② B. ②③ C. ①③ D. ①②③
D
巩固练习
2.CD为⊙O的直径,∠EOD=84°,AE交⊙O于B,且AB=OC,则∠A=_______.
28°
解析:∵OB=OC,AB=CO,∴AB=OB,∴∠A=∠BOA.
又∵OB=OE,∴∠E=∠EBO,∵∠EBO=2∠A,∴∠E=2∠A,
又∵∠EOD=∠E+∠A,∴3∠A=∠EOD,
∵∠EOD=84°,∴∠A=28°
课堂练习
2. 判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
课堂练习
3.在⊙O中,,那么( )
A.AB=2CD B.AB=CD C.AB<2CD D.AB>2CD
C
课堂练习
4.已知圆的半径,可以画____个圆;已知圆心,可以画____个圆;已知圆心和半径可以画_____个圆.
无数
无数
1
课堂练习
5.过已知⊙O上一定点P,可以画半径_____条;弦____条;直径____条.
1
无数
1
课堂练习
6.某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图27-11所示,那么运动员公寓应建立在何处?
任意作连结A、B、C三点中的两点所成的线段的中垂线的交点.
课堂练习
圆
定义
旋转定义
(描述性定义)
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
谢谢观看
第二十四章 圆
24.1 圆的有关性质
圆
01
认识圆,理解圆的定义.
02
掌握弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念,并了解它们之间的区别联系.
教学目标
情景导入
圆是一种基本的几何图形,圆形物体在生活中随处可见。
情景导入
你还能举例说出生活中还有哪些“圆”吗?
古希腊的数学家毕达哥拉斯认为:“一切立体图形中最美的是球,一切平面图形中最美的是圆”。
新知探究
圆的定义
2.问题 观察画圆的过程,你能说出圆是如何画出来的吗?
B
B
圆的旋转定义
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点所形成的图形叫做圆.
新知探究
圆的定义
圆的表示方法:在一个平面内,线段绕它固定的一个端点旋转一周,另一个端点所形成的图形叫做圆. 其固定的端点叫做圆心,线段叫做半径.
以点为圆心的圆,记作“⊙”,读作“圆”.
新知探究
圆的定义
新知探究
圆的定义
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
O
圆心相同,半径不同
半径相同,圆心不同
确定一个圆的要素
新知探究
圆的定义
圆可以看成到定点距离等于定长的所有点组成的.
满足什么条件的?
有间隙吗?
圆也可以看成是由多个点组成的
到定点的距离等于定长
的点都在同一个圆上吗?
无数个圆
无数个圆
圆心、半径都确定
新知探究
圆的定义
2.如何画一个确定的圆?
想一想:1.以1cm为半径能画几个圆,以点O为圆心能画几个圆?
新知探究
圆的定义
3.从集合角度认识圆
问题1:圆上各点到定点(圆心 O)的距离有什么规律?
问题2:到定点的距离等于定长的点又有什么特点?
·
r
O
A
新知探究
圆的定义
观察画圆过程
回答:
(1)圆上各点到定点 (圆心)的距离都等于 。
定长(半径r)
(2)到定点的距离等于定长的点都在 。
同一个圆上
圆的第二定义:
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形。
到定点的距离等于定长的点都在同一个圆上.
圆上各点到定点(圆心)的距离都等于定长(半径);
新知探究
圆的定义
动态:
总结归纳:圆的两种定义
圆心为、半径为的圆可以看成是所有到定点的距离等于定长的点的集合.
静态:
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载。它的意思是圆上各点到圆心的距离都等于半径。
小知识
新知探究
1、车轮为什么做成圆形的?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道路。
2、如果车轮做成椭圆或正方形的,坐车的人会是什么感觉?
巩固练习
如图,矩形ABCD的对角线AC、BD交于点O,求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
∴A、B、C、D在以O为圆心以OA为半径的圆上。矩形——四点共圆.
巩固练习
1、从树木的年轮,可以很清楚的看出树生长的年龄。如果一棵20年树龄的红杉树的树干直径是23cm,那么这棵红杉树的半径平均每年增加多少?
23÷20=1.15
1.15÷2=0.575
巩固练习
2、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺已不可。
周圆
位置
大小
新知探究
圆的有关概念
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
1.弦
新知探究
圆的有关概念
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
B
O
A
C
⌒
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
2.弧
新知探究
圆的有关概念
O
A
B
O
A
B
探索:圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
【发现】直径是最长的弦
新知探究
圆的有关概念
·
C
O
A
B
⌒
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
⌒
(如图中的AC)
(用三个字母表示,如图中的ACB)
3.优弧与劣弧
新知探究
圆的有关概念
·
C
O
A
B
圆心O
直径AB
弦AC
优弧ABC,记作
劣弧AC,记作
O′
半径OO′
新知探究
圆的有关概念
能够重合的两个圆是等圆。
半径相等的两个圆是等圆;
反过来说,同圆或等圆的半径相等。
4.等圆
新知探究
圆的有关概念
·
B
O1
A
在同圆或等圆中,能够互相重合的弧
·
D
O2
F
E
C
问题 长度相等的两段弧是等弧吗?为什么?
5.等弧
巩固练习
1.1.下列三个命题:①圆既是轴对称图形又是中心对称图形;②直径是弦;
③半径相等的两个半圆是等弧.其中正确的是( )
A.①② B. ②③ C. ①③ D. ①②③
D
巩固练习
2.CD为⊙O的直径,∠EOD=84°,AE交⊙O于B,且AB=OC,则∠A=_______.
28°
解析:∵OB=OC,AB=CO,∴AB=OB,∴∠A=∠BOA.
又∵OB=OE,∴∠E=∠EBO,∵∠EBO=2∠A,∴∠E=2∠A,
又∵∠EOD=∠E+∠A,∴3∠A=∠EOD,
∵∠EOD=84°,∴∠A=28°
课堂练习
2. 判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
课堂练习
3.在⊙O中,,那么( )
A.AB=2CD B.AB=CD C.AB<2CD D.AB>2CD
C
课堂练习
4.已知圆的半径,可以画____个圆;已知圆心,可以画____个圆;已知圆心和半径可以画_____个圆.
无数
无数
1
课堂练习
5.过已知⊙O上一定点P,可以画半径_____条;弦____条;直径____条.
1
无数
1
课堂练习
6.某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图27-11所示,那么运动员公寓应建立在何处?
任意作连结A、B、C三点中的两点所成的线段的中垂线的交点.
课堂练习
圆
定义
旋转定义
(描述性定义)
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
谢谢观看
同课章节目录
