17.2勾股定理的逆定理课件
文档属性
| 名称 | 17.2勾股定理的逆定理课件 |  | |
| 格式 | zip | ||
| 文件大小 | 415.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-26 11:31:11 | ||
图片预览








文档简介
课件24张PPT。在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。——毕达哥拉斯
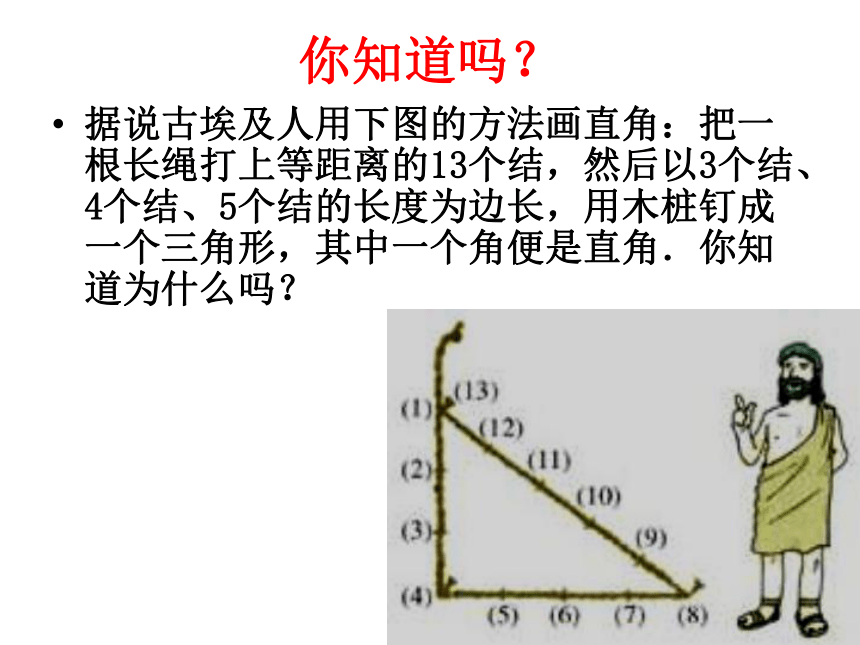
勾股定理的逆定理一:复习与巩固 你知道吗?据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你知道为什么吗? 探究 1.画图:画出边长分别是下列各组数的三角形(单位:厘米)
A:3、4、3 ;B:3、4、5;C:3、4、6;D:6、8、102.测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下:
A:_______ B:_______ C:______ D:_______
3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______ C:______ D:______ 4.找规律:根据上述每个三角形所给的各组边长请你找出最长边 的平方与其他两边的平方和之间的关系。
A:______ B:_______ C:______ D:______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是 。直角三角形钝角三角形锐角三角形直角三角形两较短边长度的平方和等于最长边长度的平方猜想命题2 如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2,互逆命题 在一对命题中,第一个命题的题设恰为第二个命题的结论,而第一个命题的结论恰为第二个命题的题设,像这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.说出下列命题的逆命题,并判断它们是否正确.1.原命题:猫有四只脚.( )
逆命题:有四只脚的是猫.( )
2.原命题:对顶角相等.( )
逆命题:相等的角是对顶角.( )
3.原命题:线段垂直平分线上的点,到这条线段两端距离相等.( )
逆命题:到线段两端距离相等的点,在这条线段的垂直平分线上.( )
4.原命题:角平分线上的点,到这个角的两边距离相等.( )
逆命题:到角两边距离相等的点,在这个角的平分线上.( )明确下面问题(1)任何一个命题都有逆命题;
(2)原命题是正确,逆命题不一定正确,原命题不正确,逆命题可能正确;
(3)原命题与逆命题的关系就是,命题中题设与结论相互转换的关系. (1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.定理与逆定理我们已经学习了一些互逆的定理,如:
两直线平行,内错角相等;内错角相等,两直线平行.想一想:
互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.勾股定理的逆命题勾股定理互逆命题已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形勾股定理的逆命题勾股定理的逆命题勾股定理互逆命题逆定理定理勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.
说明:(1)一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理为互逆定理;
(2)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(3)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据. 分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方. 例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数组. 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.到 请你找出一些勾股数组当第一个数是奇数(大于1)时,则第二个数是第一个数的平方减1再除以2,第三个数是第一个数的平方加1再除以2练一练:3,4,5;5,12,13, 6,8,10;
7,24,25;8,15,17; 9,40,41
10,24,26;11,60,61;12,35,37……当第一个数是偶数(大于2)时,则第二个数是第一个数除以2再平方后减1,第三个数是第一个数除以2平方后加1
.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗? 练一练.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为81517ABC例 一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸,这个零件符合要求吗?3451213答案:符合3.如图,在正方形ABCD中,F是CD的中点,E为BC上一点且EC= BC,求证:∠EFA=90° ADBCFE
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36课堂小结1.勾股定理的逆定理及其作用;
2.什么是互逆命题;
3.什么是互逆定理;
4.什么是勾股数.作业:84页, 习题18.2第1题、第4题
勾股定理的逆定理一:复习与巩固 你知道吗?据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你知道为什么吗? 探究 1.画图:画出边长分别是下列各组数的三角形(单位:厘米)
A:3、4、3 ;B:3、4、5;C:3、4、6;D:6、8、102.测量:用你的量角器分别测量一下上述各三角形的最大角的度数,并记录如下:
A:_______ B:_______ C:______ D:_______
3.判断:请判断一下上述你所画的三角形的形状.
A:______ B:_______ C:______ D:______ 4.找规律:根据上述每个三角形所给的各组边长请你找出最长边 的平方与其他两边的平方和之间的关系。
A:______ B:_______ C:______ D:______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样的关系时,这个三角形才可能是直角三角形呢?
你的猜想是 。直角三角形钝角三角形锐角三角形直角三角形两较短边长度的平方和等于最长边长度的平方猜想命题2 如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2,互逆命题 在一对命题中,第一个命题的题设恰为第二个命题的结论,而第一个命题的结论恰为第二个命题的题设,像这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.说出下列命题的逆命题,并判断它们是否正确.1.原命题:猫有四只脚.( )
逆命题:有四只脚的是猫.( )
2.原命题:对顶角相等.( )
逆命题:相等的角是对顶角.( )
3.原命题:线段垂直平分线上的点,到这条线段两端距离相等.( )
逆命题:到线段两端距离相等的点,在这条线段的垂直平分线上.( )
4.原命题:角平分线上的点,到这个角的两边距离相等.( )
逆命题:到角两边距离相等的点,在这个角的平分线上.( )明确下面问题(1)任何一个命题都有逆命题;
(2)原命题是正确,逆命题不一定正确,原命题不正确,逆命题可能正确;
(3)原命题与逆命题的关系就是,命题中题设与结论相互转换的关系. (1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.定理与逆定理我们已经学习了一些互逆的定理,如:
两直线平行,内错角相等;内错角相等,两直线平行.想一想:
互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.勾股定理的逆命题勾股定理互逆命题已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形勾股定理的逆命题勾股定理的逆命题勾股定理互逆命题逆定理定理勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.
说明:(1)一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理为互逆定理;
(2)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(3)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据. 分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方. 例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数组. 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.到 请你找出一些勾股数组当第一个数是奇数(大于1)时,则第二个数是第一个数的平方减1再除以2,第三个数是第一个数的平方加1再除以2练一练:3,4,5;5,12,13, 6,8,10;
7,24,25;8,15,17; 9,40,41
10,24,26;11,60,61;12,35,37……当第一个数是偶数(大于2)时,则第二个数是第一个数除以2再平方后减1,第三个数是第一个数除以2平方后加1
.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗? 练一练.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为81517ABC例 一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边尺寸,这个零件符合要求吗?3451213答案:符合3.如图,在正方形ABCD中,F是CD的中点,E为BC上一点且EC= BC,求证:∠EFA=90° ADBCFE
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36课堂小结1.勾股定理的逆定理及其作用;
2.什么是互逆命题;
3.什么是互逆定理;
4.什么是勾股数.作业:84页, 习题18.2第1题、第4题
