3.3.2抛物线的简单几何性质 课件(共22张PPT)人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.3.2抛物线的简单几何性质 课件(共22张PPT)人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 30.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 23:31:13 | ||
图片预览






文档简介
(共22张PPT)
3.3.2抛物线的简单几何性质
第三章 圆锥曲线的方程
复习回顾
定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线(parabola).点F叫做抛物线的焦点,直线l叫做抛物线的准线.
图像 标准方程 焦点坐标 准线方程
探究新知
追问 那其他的形式的抛物线方程呢?
当x的值增大时, y 的值也增大,这说明抛物线向右上方和右下方无限延伸.
1. 范围
K
F
M(x,y)
x
y
O
H
M′(x,-y)
关于x轴对称
即点(x,-y)也在抛物线上,
故抛物线y2 =2px(p>0)关于x轴对称.
则(-y)2 = 2px ,
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
我们把抛物线的对称轴叫做抛物线的轴.
4.离心率
探究新知
3.顶点
定义:抛物线与它的轴的交点叫做抛物线的顶点.
∴ y2 =2px(p>0)中,令y=0,则x=0.
即抛物线y2 =2px(p>0)的顶点(0,0).
K
F
M
x
y
O
H
由定义知, 抛物线的离心率为e=1.
抛物线上的点M与焦点F的距离和它到准线的距离d之比 ,叫做抛物线的离心率,用e表示.
探究新知
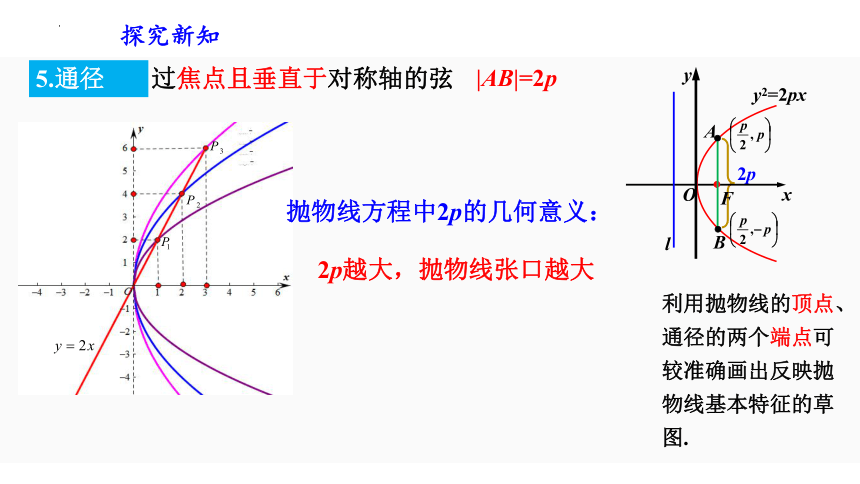
过焦点且垂直于对称轴的弦
|AB|=2p
5.通径
A
B
y2=2px
2p
x
l
F
y
O
抛物线方程中2p的几何意义:
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
2p越大,抛物线张口越大
探究新知
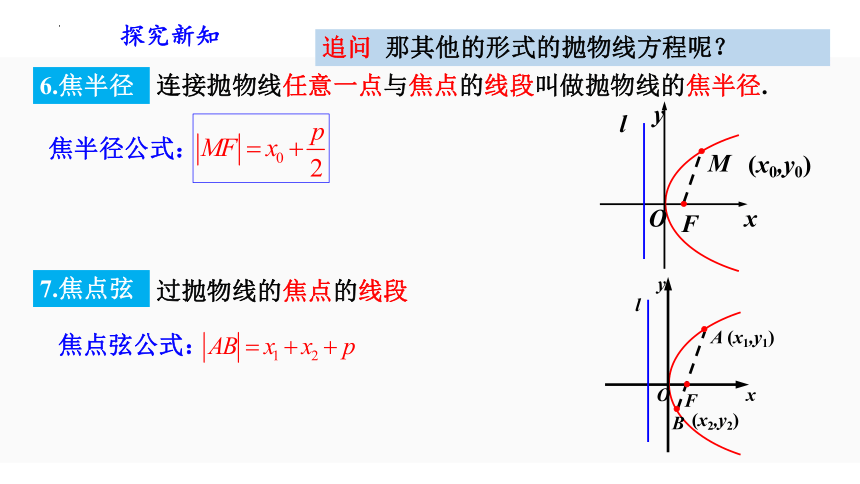
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径.
焦半径公式:
6.焦半径
x
l
F
M
y
O
(x0,y0)
追问 那其他的形式的抛物线方程呢?
x
l
F
A
y
O
B
(x1,y1)
(x2,y2)
焦点弦公式:
7.焦点弦
过抛物线的焦点的线段
(1) 抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2) 抛物线只有一条对称轴,没有对称中心;
(3) 抛物线只有一个顶点,一个焦点,一条准线;
(4) 抛物线的离心率e是确定的为1,
(5) 抛物线的通径为2p, 2p越大,抛物线的张口越大.
归纳
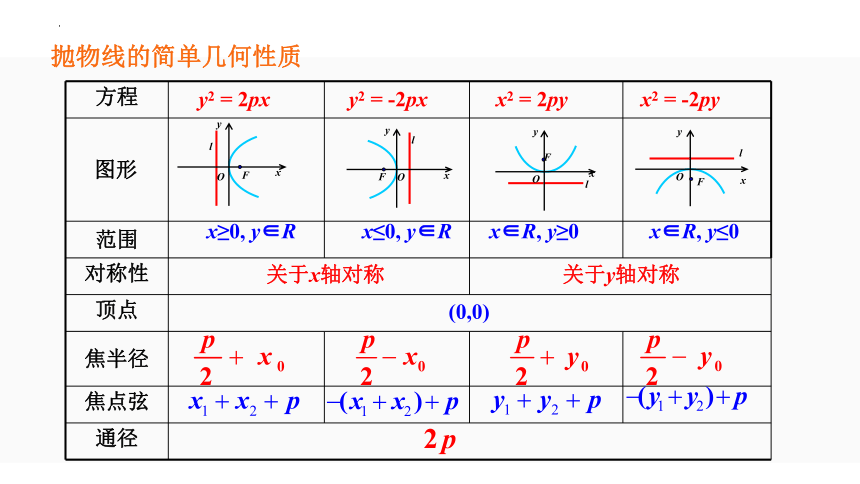
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
例题讲解
l
l
例1 已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程.
因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过M(2, ),
解:
所以设方程为:
又因为点M在抛物线上,
所以:
因此所求抛物线标准方程为:
例题讲解
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
例题讲解
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
解法1(代数法): 由题意知:抛物线的焦点 F(1 , 0),
联立得:
例题讲解
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
解法2(几何法(数形结合)):
由题意可知,,=1,焦点F的坐标为,准线方程为. 如图,设A() , B(),A,B两点到准线的距离分别为.
由抛物线的定义可知,
于是得.
因为直线l的斜率为1,且过焦点,∴直线的方程为 ①
将①代入方程,得
化简,得
所以=6,.
所以,线段AB的长是8.
例题讲解
课堂小结
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
探究新知
1.抛物线的焦半径、焦点弦长公式
特别的:焦点弦垂直抛物线的对称轴,则其称为通径,长为2P(最短).
2.抛物线的焦半径长的倒数和是定值
3.过抛物线的焦点的直线与抛物线交于
O
x
y
B
A
F
直线的反斜截式(优越性)
探究新知
4.以抛物线的焦点弦为直径的圆与准线相切
探究新知
直线与圆锥曲线的有关综合问题,我们已经接触了一些,在我们看来就是三句话的实践:
(一)设而不求;
(二)联立方程组,根与系数的关系;
(三)大胆计算分析,数形结合活思维.
x
y
O
直线与抛物线位置关系种类
1.相离(0个交点);
2.相切(1个交点) ;
3.相交(1个交点,2个交点)
例题讲解
⑴只有一个公共点
⑵有两个公共点
⑶没有公共点
例2
三、判断直线与抛物线位置关系的操作程序(一)
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
例题讲解
3.3.2抛物线的简单几何性质
第三章 圆锥曲线的方程
复习回顾
定义:我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线(parabola).点F叫做抛物线的焦点,直线l叫做抛物线的准线.
图像 标准方程 焦点坐标 准线方程
探究新知
追问 那其他的形式的抛物线方程呢?
当x的值增大时, y 的值也增大,这说明抛物线向右上方和右下方无限延伸.
1. 范围
K
F
M(x,y)
x
y
O
H
M′(x,-y)
关于x轴对称
即点(x,-y)也在抛物线上,
故抛物线y2 =2px(p>0)关于x轴对称.
则(-y)2 = 2px ,
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
我们把抛物线的对称轴叫做抛物线的轴.
4.离心率
探究新知
3.顶点
定义:抛物线与它的轴的交点叫做抛物线的顶点.
∴ y2 =2px(p>0)中,令y=0,则x=0.
即抛物线y2 =2px(p>0)的顶点(0,0).
K
F
M
x
y
O
H
由定义知, 抛物线的离心率为e=1.
抛物线上的点M与焦点F的距离和它到准线的距离d之比 ,叫做抛物线的离心率,用e表示.
探究新知
过焦点且垂直于对称轴的弦
|AB|=2p
5.通径
A
B
y2=2px
2p
x
l
F
y
O
抛物线方程中2p的几何意义:
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
2p越大,抛物线张口越大
探究新知
连接抛物线任意一点与焦点的线段叫做抛物线的焦半径.
焦半径公式:
6.焦半径
x
l
F
M
y
O
(x0,y0)
追问 那其他的形式的抛物线方程呢?
x
l
F
A
y
O
B
(x1,y1)
(x2,y2)
焦点弦公式:
7.焦点弦
过抛物线的焦点的线段
(1) 抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2) 抛物线只有一条对称轴,没有对称中心;
(3) 抛物线只有一个顶点,一个焦点,一条准线;
(4) 抛物线的离心率e是确定的为1,
(5) 抛物线的通径为2p, 2p越大,抛物线的张口越大.
归纳
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
例题讲解
l
l
例1 已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2, ),求它的标准方程.
因为抛物线关于x轴对称,它的顶点在坐标原点,并且经过M(2, ),
解:
所以设方程为:
又因为点M在抛物线上,
所以:
因此所求抛物线标准方程为:
例题讲解
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
例题讲解
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
解法1(代数法): 由题意知:抛物线的焦点 F(1 , 0),
联立得:
例题讲解
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
解法2(几何法(数形结合)):
由题意可知,,=1,焦点F的坐标为,准线方程为. 如图,设A() , B(),A,B两点到准线的距离分别为.
由抛物线的定义可知,
于是得.
因为直线l的斜率为1,且过焦点,∴直线的方程为 ①
将①代入方程,得
化简,得
所以=6,.
所以,线段AB的长是8.
例题讲解
课堂小结
方程
图形
范围
对称性
顶点
焦半径
焦点弦
通径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
x≥0, y∈R
x≤0, y∈R
x∈R, y≥0
x∈R, y≤0
l
F
y
x
O
关于x轴对称
关于y轴对称
(0,0)
抛物线的简单几何性质
探究新知
1.抛物线的焦半径、焦点弦长公式
特别的:焦点弦垂直抛物线的对称轴,则其称为通径,长为2P(最短).
2.抛物线的焦半径长的倒数和是定值
3.过抛物线的焦点的直线与抛物线交于
O
x
y
B
A
F
直线的反斜截式(优越性)
探究新知
4.以抛物线的焦点弦为直径的圆与准线相切
探究新知
直线与圆锥曲线的有关综合问题,我们已经接触了一些,在我们看来就是三句话的实践:
(一)设而不求;
(二)联立方程组,根与系数的关系;
(三)大胆计算分析,数形结合活思维.
x
y
O
直线与抛物线位置关系种类
1.相离(0个交点);
2.相切(1个交点) ;
3.相交(1个交点,2个交点)
例题讲解
⑴只有一个公共点
⑵有两个公共点
⑶没有公共点
例2
三、判断直线与抛物线位置关系的操作程序(一)
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
例题讲解
