勾股定理(吉林省白山市临江市)
文档属性
| 名称 | 勾股定理(吉林省白山市临江市) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-29 00:00:00 | ||
图片预览



文档简介
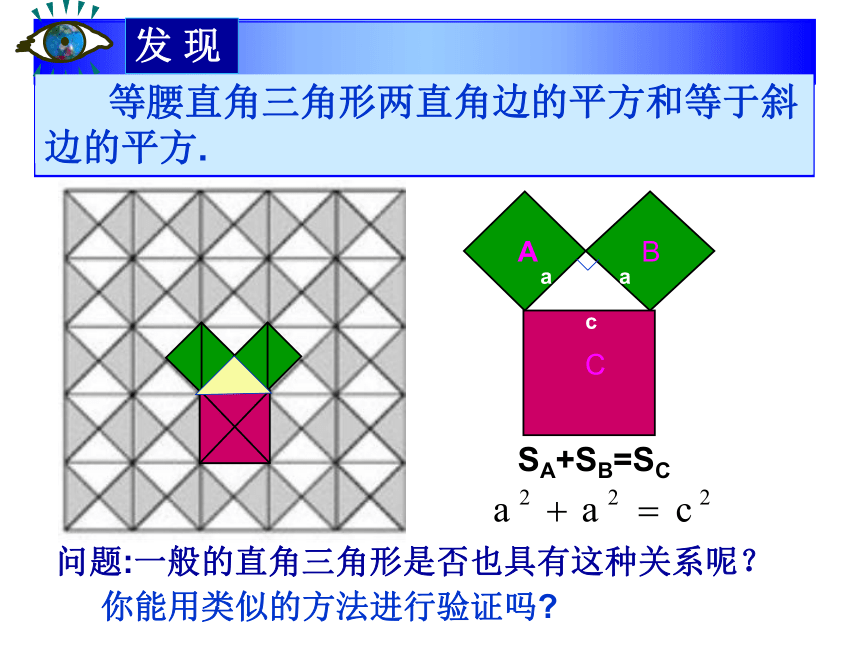
课件19张PPT。欢迎参加《数学》大课堂! 毕达哥拉斯,(公元前572-前492年) ,古希腊著名的数学家、哲学家、天文学家。毕达哥拉斯SA+SB=SC1.在这张图中,你发现了哪些基本图形?2.毕达哥拉斯发现了与三角形相邻的正方形面积有一种特殊的关系.你发现了吗?3.从而毕达哥拉斯就得出了等腰直角三角形三边的某种数量关系.你觉得是什么关系?发 现 等腰直角三角形两直角边的平方和等于斜边的平方.问题:一般的直角三角形是否也具有这种关系呢?你能用类似的方法进行验证吗?ABC4913sA+sB=sC 一般的直角三角形同样也具有这种关系.图1
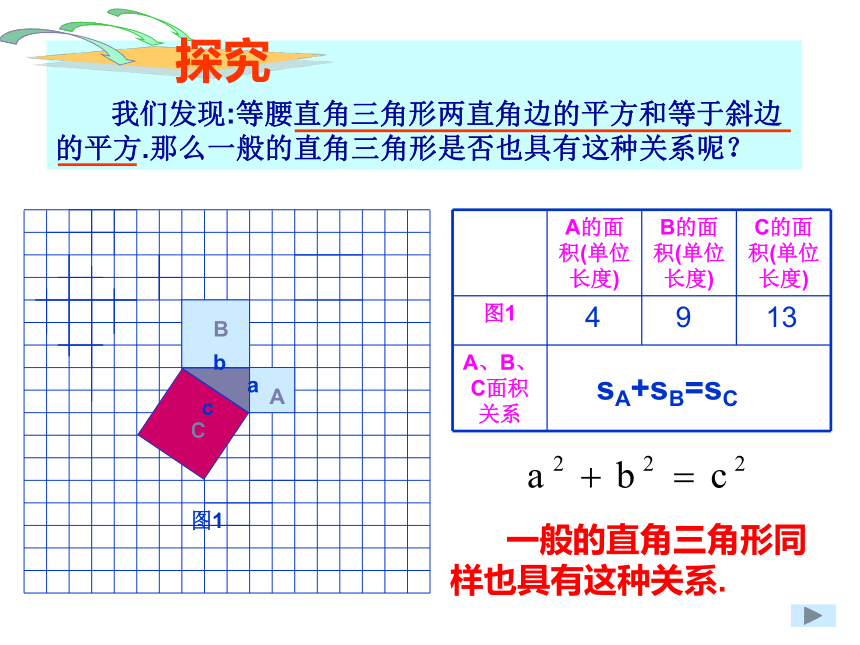
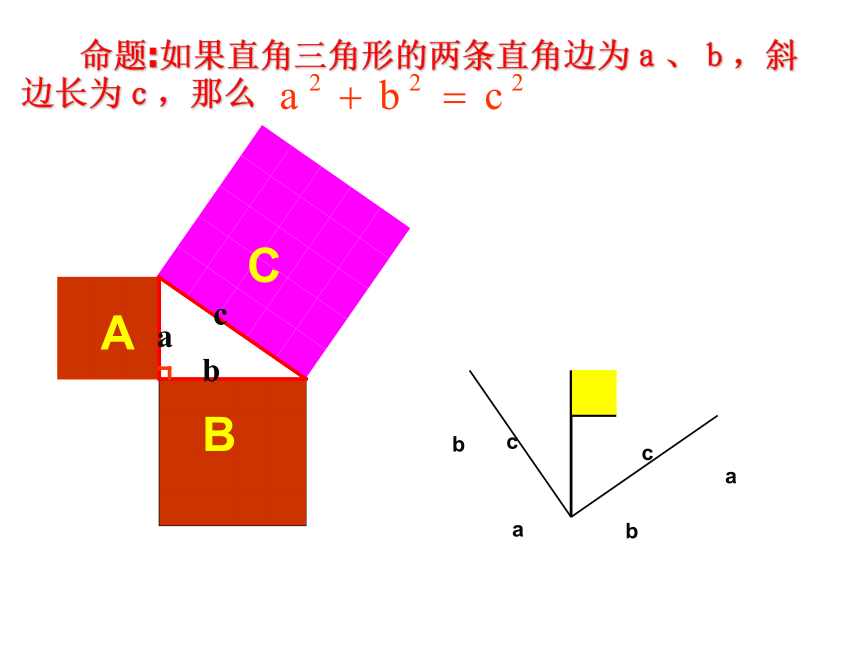
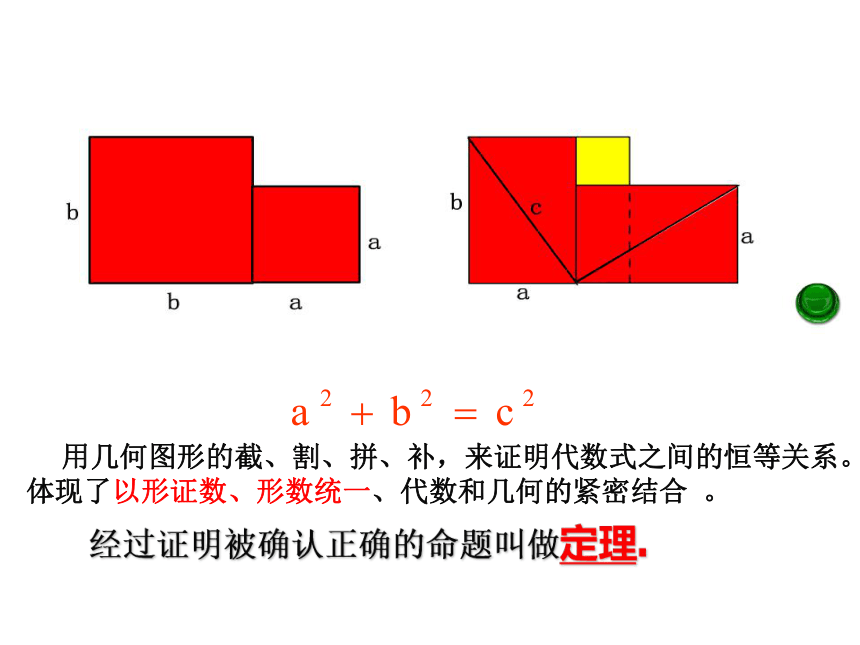
我们发现:等腰直角三角形两直角边的平方和等于斜边的平方.那么一般的直角三角形是否也具有这种关系呢? 命题:如果直角三角形的两条直角边为a、b,斜边长为c,那么cabbbaacc经过证明被确认正确的命题叫做定理. 用几何图形的截、割、拼、补,来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。赵爽弦图赵爽:东汉末至三国时代吴国人.
为《周髀算经》作注,并著有《勾股圆方图》 。这是我国对勾股定理最早的证明。
表现了我国古人对数学的钻研精神和聪明才智. 2002年国际数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。 在西方,勾股定理又被称为“毕达哥拉斯定理”, “百牛定理”, “驴桥定理”.大正方形的面积可以表示为 —————————— 又可以表示为:———————(a+b)2拼一拼
你还能用4个全等的直角三角形围出一个以两直角边的和为边长的大正方形吗?你还能用它说明勾股定理吗?例1:求下图中字母A、B所代表的正方形的面积. 请你欣赏毕达哥拉斯树在本节课中,我们……1.本节主线2.学习内容及方法 学习了著名的勾股定理,还知道从特殊到一般的探索方法.3.本节的数学思想 借助于图形的面积来探索、验证数学结论的数形结合思想。4.学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现.这节课我们还认识了两位伟大的数学家,受到了数学文化辉煌历史的教育。布置作业1.必答题:课本第77页第1. 2题.
2选做题:(一)通过查阅资料,了解勾股定理的文化背景。(二):通过查阅资料,收集勾股定理的证明方法。 (任选其一)
3.实践题:尝试用七巧板拼图,验证勾股定理.
勾股定理的文化价值(1) 勾股定理是联系数学中数与形的第一定理。(2) 勾股定理反映了自然界基本规律,有文明的宇宙“人”都应该认识它,因而勾股定理图被建议作为与“外星人”联系的信号。(3)勾股定理导致不可通约量的发现,引发第一次数学危机。(4)勾股定理公式是第一个不定方程,为不定方程的解题程序树立了一个范式。美国总统的证明茄菲尔德 (James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关证明aabbcc1881年,茄菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。∟∟∟拼图游戏
我们发现:等腰直角三角形两直角边的平方和等于斜边的平方.那么一般的直角三角形是否也具有这种关系呢? 命题:如果直角三角形的两条直角边为a、b,斜边长为c,那么cabbbaacc经过证明被确认正确的命题叫做定理. 用几何图形的截、割、拼、补,来证明代数式之间的恒等关系。体现了以形证数、形数统一、代数和几何的紧密结合 。赵爽弦图赵爽:东汉末至三国时代吴国人.
为《周髀算经》作注,并著有《勾股圆方图》 。这是我国对勾股定理最早的证明。
表现了我国古人对数学的钻研精神和聪明才智. 2002年国际数学家大会在北京召开,这届大会会标的中央图案正是经过艺术处理的“弦图”,标志着中国古代数学成就。 在西方,勾股定理又被称为“毕达哥拉斯定理”, “百牛定理”, “驴桥定理”.大正方形的面积可以表示为 —————————— 又可以表示为:———————(a+b)2拼一拼
你还能用4个全等的直角三角形围出一个以两直角边的和为边长的大正方形吗?你还能用它说明勾股定理吗?例1:求下图中字母A、B所代表的正方形的面积. 请你欣赏毕达哥拉斯树在本节课中,我们……1.本节主线2.学习内容及方法 学习了著名的勾股定理,还知道从特殊到一般的探索方法.3.本节的数学思想 借助于图形的面积来探索、验证数学结论的数形结合思想。4.学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现.这节课我们还认识了两位伟大的数学家,受到了数学文化辉煌历史的教育。布置作业1.必答题:课本第77页第1. 2题.
2选做题:(一)通过查阅资料,了解勾股定理的文化背景。(二):通过查阅资料,收集勾股定理的证明方法。 (任选其一)
3.实践题:尝试用七巧板拼图,验证勾股定理.
勾股定理的文化价值(1) 勾股定理是联系数学中数与形的第一定理。(2) 勾股定理反映了自然界基本规律,有文明的宇宙“人”都应该认识它,因而勾股定理图被建议作为与“外星人”联系的信号。(3)勾股定理导致不可通约量的发现,引发第一次数学危机。(4)勾股定理公式是第一个不定方程,为不定方程的解题程序树立了一个范式。美国总统的证明茄菲尔德 (James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关证明aabbcc1881年,茄菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。∟∟∟拼图游戏
