18.1.1 平行四边形及其性质(一) 课件
文档属性
| 名称 | 18.1.1 平行四边形及其性质(一) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 217.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-01 16:18:47 | ||
图片预览



文档简介
(共12张PPT)
18.1.1 平行四边形及其性质(一)
1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
学习重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
学习难点:运用平行四边形的性质进行有关的论证和计算.
学习目标:
学习过程:
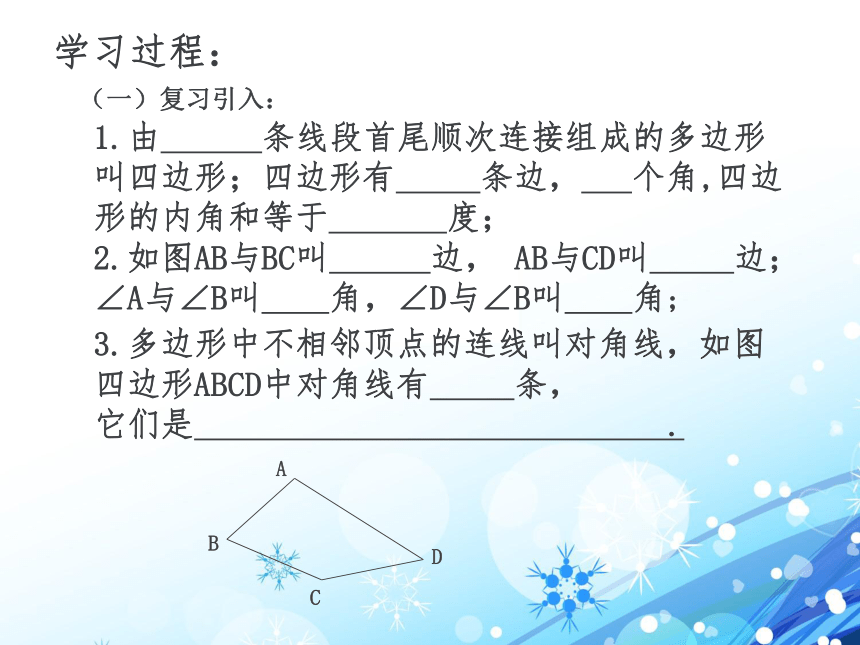
(一)复习引入:
1.由 条线段首尾顺次连接组成的多边形叫四边形;四边形有 条边, 个角,四边形的内角和等于 度;
2.如图AB与BC叫 边, AB与CD叫 边;∠A与∠B叫 角,∠D与∠B叫 角;
3.多边形中不相邻顶点的连线叫对角线,如图四边形ABCD中对角线有 条,
它们是 .
A
B
C
D
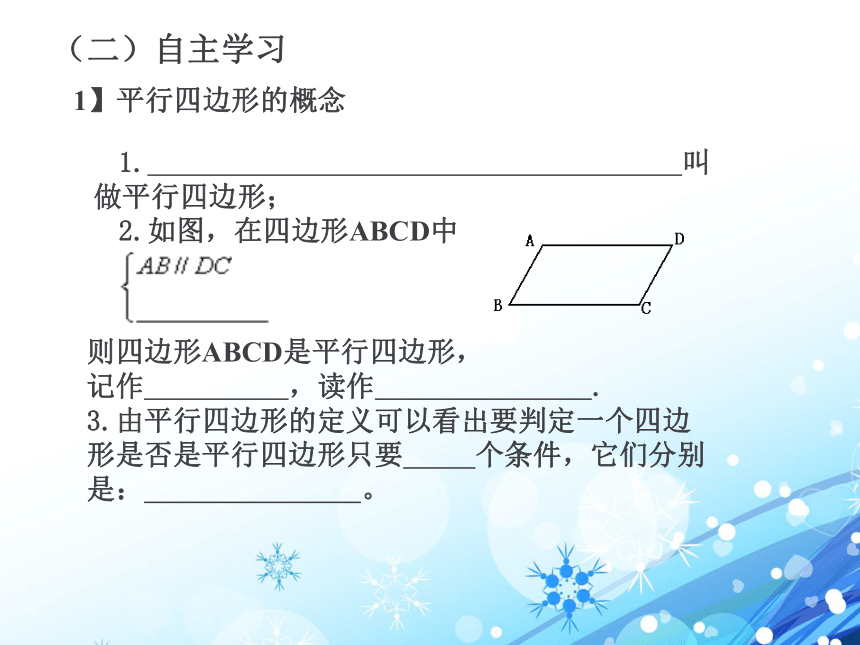
(二)自主学习
1】平行四边形的概念
1. 叫做平行四边形;
2.如图,在四边形ABCD中
则四边形ABCD是平行四边形,
记作 ,读作 .
3.由平行四边形的定义可以看出要判定一个四边形是否是平行四边形只要 个条件,它们分别是: 。
2】如图探究
(两直线平行, )。
∵BC// ,
(两直线平行, )
∴
∵AB// ,
∴
∴
( )
∴
,
即
≌
∴
1
2
3
4
A
B
C
D
∵ AC=CA
通过探究发现平行
四边形的边、角有什么样的关系?
归纳总结
平行四边形的性质有:
性质1: 平行四边形的对边相等.
性质2: 平行四边形的对角相等.
(三)合作探究
1.在□ ABCD中,∠A:∠B=2:3,则∠A= ,∠B= ,∠C= , ∠D= .
2.已知□ ABCD的周长为20cm,且AD-AB=1cm,则 AD= ,CD= .
5.5cm
4.5cm
3.判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( ) (2)平行四边形的四个内角都相等. ( ) (3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( ) (6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
(四)达标检测
当堂小结
1. 概念:
四边形
两组对边
平行四边形
分别平行
2. 性质:
性质一:对边平行,相等
性质二:对角相等,邻角互补
3. 两平行线的距离相等
18.1.1 平行四边形及其性质(一)
1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
学习重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
学习难点:运用平行四边形的性质进行有关的论证和计算.
学习目标:
学习过程:
(一)复习引入:
1.由 条线段首尾顺次连接组成的多边形叫四边形;四边形有 条边, 个角,四边形的内角和等于 度;
2.如图AB与BC叫 边, AB与CD叫 边;∠A与∠B叫 角,∠D与∠B叫 角;
3.多边形中不相邻顶点的连线叫对角线,如图四边形ABCD中对角线有 条,
它们是 .
A
B
C
D
(二)自主学习
1】平行四边形的概念
1. 叫做平行四边形;
2.如图,在四边形ABCD中
则四边形ABCD是平行四边形,
记作 ,读作 .
3.由平行四边形的定义可以看出要判定一个四边形是否是平行四边形只要 个条件,它们分别是: 。
2】如图探究
(两直线平行, )。
∵BC// ,
(两直线平行, )
∴
∵AB// ,
∴
∴
( )
∴
,
即
≌
∴
1
2
3
4
A
B
C
D
∵ AC=CA
通过探究发现平行
四边形的边、角有什么样的关系?
归纳总结
平行四边形的性质有:
性质1: 平行四边形的对边相等.
性质2: 平行四边形的对角相等.
(三)合作探究
1.在□ ABCD中,∠A:∠B=2:3,则∠A= ,∠B= ,∠C= , ∠D= .
2.已知□ ABCD的周长为20cm,且AD-AB=1cm,则 AD= ,CD= .
5.5cm
4.5cm
3.判断题:(对的在括号内填“√”,错的填“×”)
(1)平行四边形两组对边分别平行且相等. ( ) (2)平行四边形的四个内角都相等. ( ) (3)平行四边形的相邻两个内角的和等于180°( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( ) (6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
(四)达标检测
当堂小结
1. 概念:
四边形
两组对边
平行四边形
分别平行
2. 性质:
性质一:对边平行,相等
性质二:对角相等,邻角互补
3. 两平行线的距离相等
