平行四边形的性质1
图片预览








文档简介
课件21张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么.
——毕达哥拉斯 问题不在于告诉他一个真理,而在于
教他怎样发现真理.
——卢梭探索真理比占有真理更重要.
——爱因斯坦19.1.1 平行四边形的性质南昌第十三中学 徐春梅观察——思考观察——思考拼 一 拼 取两个全等的三角形纸片,将它们的相等的一边重合,得到一个四边形。
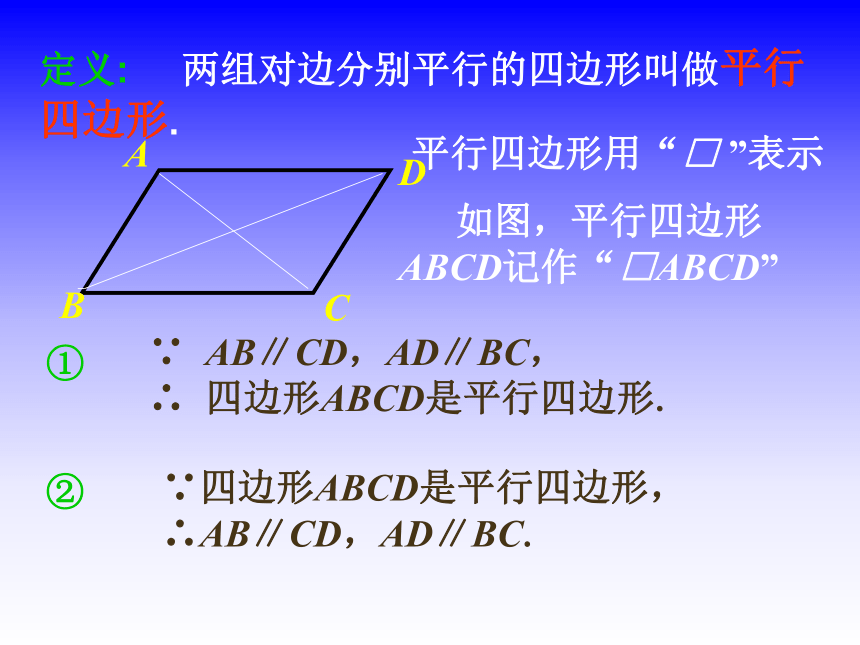
你拼出了怎样的四边形?拼 一 拼 定义: 两组对边分别平行的四边形叫做平行四边形. 如图,平行四边形ABCD记作“□ABCD” ①∵ AB∥CD,AD∥BC,
∴ 四边形ABCD是平行四边形.②∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
平行四边形用“□ ”表示 (1)根据定义画一个平行四边形.
(2)观察这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?
(3)度量一下,是不是和你的猜想一致?演 示平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互余转一转 如图,连接AC
∵ 四边形ABCD是平行四边形
∴ AD∥BC,AB ∥CD(平行四边形的定义)
∴ ∠1=∠2,∠3=∠4
又知AC是公共边
∴ △ABC≌△CDA(ASA)
∴ AD=BC,AB=CD
∠B=∠D推理你可以证明∠BAD=∠BCD吗?平行四边形的对边相等;平行四边形的对角相等.例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:
∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36,
∴ AD=BC=10(m).2.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;
(2)边AB,BC的长度.解:(1)∵四边形ABCD是平行四边形∴∠B=∠ADC AB∥CD∴∠B+∠BCD=180°∵∠B=56°∴∠ADC=∠B=56°∠BCD=180°-∠B=180°-56°=124°(2)∵四边形ABCD是平行四边形∴AD=BC,AB=CD(平行四边形对边相等)∵AD=30,CD=25 ∴BC=30,AB=25.补充题思 考
已知平行四边形一个内角的度数,
你能确定其他内角的度数吗??α)1、□ABCD中,AB=5,BC=3,求它的周长.练一练) 2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.
(1)线段AD和BC的长度有什么关系?为什么?α(2)若这个四边形的一个外角∠α=38°,这个四边形的每个内角的度数分别是多少?为什么?BACD课堂总结你在本节课中有哪些收获?1、平行四边形的定义、符号表示法;
2、平行四边形的性质
平行四边形的对边相等;
平行四边形的对角相等.
3、平行四边形性质的应用
平行四边形的性质是今后证明线段相等和角相等的又一重要依据.
4、在平行四边形性质证明过程中添加辅助线的方法.
提炼升华 1. P93 练习,
2. P99-100,
1、2、6作 业
——毕达哥拉斯 问题不在于告诉他一个真理,而在于
教他怎样发现真理.
——卢梭探索真理比占有真理更重要.
——爱因斯坦19.1.1 平行四边形的性质南昌第十三中学 徐春梅观察——思考观察——思考拼 一 拼 取两个全等的三角形纸片,将它们的相等的一边重合,得到一个四边形。
你拼出了怎样的四边形?拼 一 拼 定义: 两组对边分别平行的四边形叫做平行四边形. 如图,平行四边形ABCD记作“□ABCD” ①∵ AB∥CD,AD∥BC,
∴ 四边形ABCD是平行四边形.②∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
平行四边形用“□ ”表示 (1)根据定义画一个平行四边形.
(2)观察这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?
(3)度量一下,是不是和你的猜想一致?演 示平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互余转一转 如图,连接AC
∵ 四边形ABCD是平行四边形
∴ AD∥BC,AB ∥CD(平行四边形的定义)
∴ ∠1=∠2,∠3=∠4
又知AC是公共边
∴ △ABC≌△CDA(ASA)
∴ AD=BC,AB=CD
∠B=∠D推理你可以证明∠BAD=∠BCD吗?平行四边形的对边相等;平行四边形的对角相等.例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:
∵ 四边形ABCD是平行四边形,
∴AB=CD, AD=BC.
∵AB=8,
∴CD=8(m)
又AB+BC+CD+AD=36,
∴ AD=BC=10(m).2.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;
(2)边AB,BC的长度.解:(1)∵四边形ABCD是平行四边形∴∠B=∠ADC AB∥CD∴∠B+∠BCD=180°∵∠B=56°∴∠ADC=∠B=56°∠BCD=180°-∠B=180°-56°=124°(2)∵四边形ABCD是平行四边形∴AD=BC,AB=CD(平行四边形对边相等)∵AD=30,CD=25 ∴BC=30,AB=25.补充题思 考
已知平行四边形一个内角的度数,
你能确定其他内角的度数吗??α)1、□ABCD中,AB=5,BC=3,求它的周长.练一练) 2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.
(1)线段AD和BC的长度有什么关系?为什么?α(2)若这个四边形的一个外角∠α=38°,这个四边形的每个内角的度数分别是多少?为什么?BACD课堂总结你在本节课中有哪些收获?1、平行四边形的定义、符号表示法;
2、平行四边形的性质
平行四边形的对边相等;
平行四边形的对角相等.
3、平行四边形性质的应用
平行四边形的性质是今后证明线段相等和角相等的又一重要依据.
4、在平行四边形性质证明过程中添加辅助线的方法.
提炼升华 1. P93 练习,
2. P99-100,
1、2、6作 业
