数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标 课件(共43张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标 课件(共43张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 09:34:51 | ||
图片预览










文档简介
(共43张PPT)
第二章 直线和圆的方程
2.3.1 两条直线的交点坐标
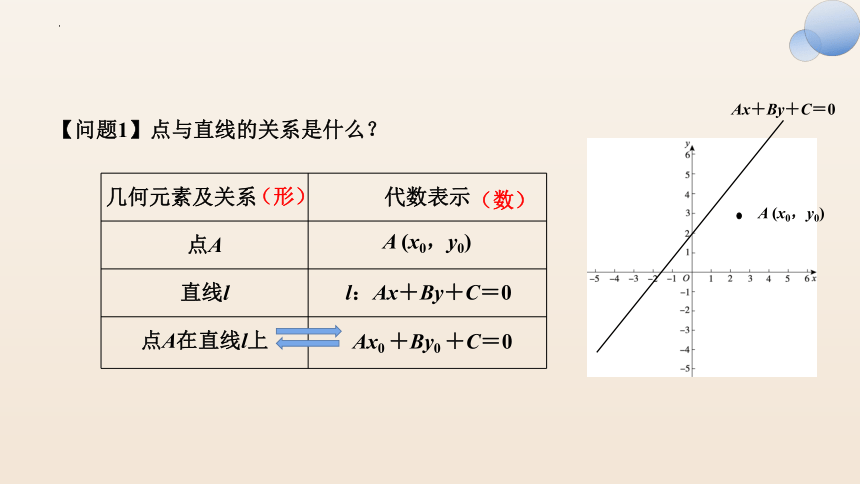
几何元素及关系 代数表示
点A
直线l
点A在直线l上
(形)
(数)
A (x0,y0)
l:Ax+By+C=0
Ax0 +By0 +C=0
【问题1】点与直线的关系是什么?
A (x0,y0)
Ax+By+C=0
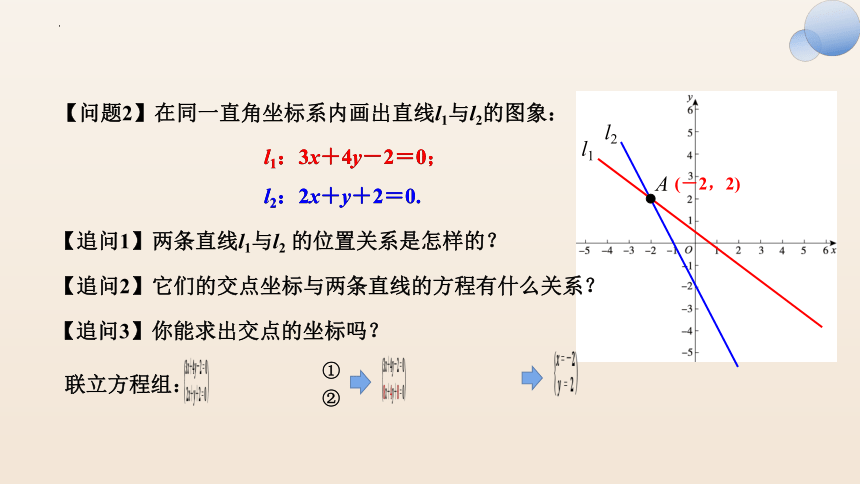
【问题2】在同一直角坐标系内画出直线l1与l2的图象:
l1:3x+4y-2=0;
【追问1】两条直线l1与l2 的位置关系是怎样的?
【追问2】它们的交点坐标与两条直线的方程有什么关系?
【追问3】你能求出交点的坐标吗?
l2
l1
A
(-2,2)
联立方程组:
①
②
l2:2x+y+2=0.
l1:3x+4y-2=0;
l2:2x+y+2=0.
【问题3】上述结论有一般性吗?
若两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0相交,它们的交点坐标与直线的方程有什么关系?由此能得出求其交点坐标的方法吗?
直线l1和l2相交
直线l1和l2存在唯一交点, 记为A(x0,y0)
点A(x0,y0)既在l1上,又在l2上
【问题3】上述结论有一般性吗?
若两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0相交,
它们的交点坐标与直线的方程有什么关系?由此能得出求其
交点坐标的方法吗?
几何元素及关系(形) 代数表示(数)
直线l1与l2的交点是A(x0,y0)
方程组
的唯一解是
l2
l1
【问题4】已知两条直线:l1:4x+2y-3=0;l2:2x+y+2=0,则这两条直线的位置关系是什么?
【追问】能否判断对应方程组解的情况?
没有公共点
方程组无解
不存在点同时满足两条直线方程
l1 ∥ l2
方程组无解
l1 ∥ l2
【问题5】已知两条直线:l1:4x+2y+4=0;l2:2x+y+2=0,则这两条直线的位置关系是什么?
l2
l1
有无数个公共点
存在无数个点同时满足两条直线方程
方程组有无数组解
直线l1和l2重合
方程组有无数组解
l1 和 l2重合
【问题6】一般地,对于两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0 ,你能说出这两条直线的位置关系与对应方程组 的解之间的联系吗?
直线的位置关系 公共点的个数 方程组解的个数 图 例
相 交
平 行
重 合
有且仅有1个
唯一解
0 个
无 解
无数个
无数组解
【问题7】(1) l1:3x+4y-2=0,l2:2x+y+2=0
(2) l1:4x+2y+3=0,l2:2x+y+2=0
(3) l1:4x+2y+4=0,l2:2x+y+2=0
对于以上三组直线,你还有其他方法判断每组直线间的位置关系么?
【追问1】能否用斜率判断两条直线的位置关系?
两直线斜率均不存在
垂直于 x 轴
截距相等重合
截距不等平行
一条斜率不存在
一条斜率存在
两直线斜率均存在
斜率不等相交
斜率相等看截距
截距相等重合
截距不等平行
两条直线相交
【问题7】(1) l1:3x+4y-2=0,l2:2x+y+2=0
(2) l1:4x+2y+3=0,l2:2x+y+2=0
(3) l1:4x+2y+4=0,l2:2x+y+2=0
对于以上三组直线,你还有其他方法判断每组直线间的位置关系么?
【追问2】如何从直线方程的一般式中确定斜率?
l1:yl2:y
k1≠k2
相交
l1:yl2:y
k1=k2b1≠b2
平行
l1:yl2:y
k1=k2b1=b2
重合
斜截式
【问题8】比较用斜率判断和解方程组判断两直线位置关系,你有什么体会?
代数方法
关注直线方程系数关系,快速判断两条直线平行、重合或相交(垂直).
解方程组判断
斜率判断
关注解的个数与交点个数的对应,判断两条直线平行、重合或相交;
求相交直线的交点坐标.
【问题9】判断两条直线的位置关系,直线方程的系数需要满足怎样的特征?
两直线位置关系 方程系数特征
相交
平行
重合
【例1】 判断下列各对直线的位置关系.如果相交,求出交点的坐标.
(1) l1:x-y=0;l2:3x+3y-10=0.
(2) l1:3x-y +4=0;l2:6x-2y-1=0.
(3) l1:3x+4 y-5=0;l2:6x+8y-10=0.
【例2】求经过直线3x-2y+1=0和直线x+3y+4=0的交点,并且平行于
直线x-y+4=0的直线方程.
【追问1】求解直线方程需要具备哪些条件?
【追问2】分析本题中的条件,可以获得哪些确定直线的信息?
交点坐标(-1,-1)
因为所求直线与xy+4=0平行,故直线的斜率为k=1
设直线方程为:y (1)=x (1),
整理得: x
解:
【问题10】方程3x+4y-2+λ(2x+y+2)=0,当λ变化时表示什么图形?该图形有何特点?
令λ=0,方程化为3x+4y-2=0,此时的图形是一条直线;
令λ=1,得到5x+5y=0,也是一条直线,(-2,2);
令λ= - 1,则x+3y-4=0,还是一条直线, (-2,2).
……
猜想:
当λ变化时,方程表示的是相交于点(-2,2)的直线
(-2,2)
(-2,2)
(-2,2)
【问题10】方程3x+4y-2+λ(2x+y+2)=0,当λ变化时表示什么图形?该图形有何特点?
(3+2λ)x+(4+λ)y+2λ-2=0
Ax+By+C=0
直线
3x+4y-2+λ(2x+y+2)=0
联立方程组:
解得交点坐标为(-2,2).
(3+2λ)x+(4+λ)y+2λ-2=0
λ
无解
经过两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点的直线系方程可以表示为:
A1x+B1y +C1 +λ(A2x+B2y +C2 )=0
求相交直线交点坐标
判断两条直线的位置关系
(相交、平行、重合)
解方程组
思想方法
数形结合
特殊到一般
问题导入
问题1:如下图已知平面内两点P1(x1,y1), P2(x2,y2) ,如何求P1, P2间的距离?
y
x
o
P2
P1
特别地, 原点O(0, 0)与任一点P(x, y)间的距离为:
求|P1P2|转化为求向量的模:
问题导入
k是直线P1P2的斜率则两点间距离公式有如下变形:
(1)当P1P2与x轴平行或重合时,
(2)当P1P2与y轴平行或重合时,
问题2:还有其它推导两点间的距离公式的方法吗?
问题导入
|P1P2|=|x2-x1|;
|P1P2|=|y2-y1|;
问题导入
问题2:还有其它推导两点间的距离公式的方法吗?
如右图,我们以P1P2为斜边构造一个直角三角形1P2Q,则点Q的坐标为(),
由勾股定理得:
∴平面内两点P1(x1, y1), P2(x2, y2)间的距离公式为:
一般选择与坐标轴平行(或垂直)的直线构造直角三角形(相应的长度易用坐标表示。)
(3)当P1P2与轴、y轴都不平行时
思考:在推导两点间距离公式时,勾股定理法与向量法比较,你有什么体会?
问题导入
用勾股定理推导平面上两点间的距离公式,不仅需要分情况讨论,还需要添加辅助线构造直角三角形,而向量法比用勾股定理推导方法简洁.
课堂练习P74
典型例题
例3 已知点A(-1,2),B(2, ),在轴上求一点P,使|PA|=|PB|,并求|PA|的值.
一题多解
例3 已知点A(-1,2),B(2, ),在轴上求一点P,使|PA|=|PB|,并求|PA|的值.
这个题目还有其他解法吗?看到 “|PA|=|PB|”,你想到了什么?
点P可以看成是线段AB的垂直平分线与轴的交点!
课堂练习P79
典型例题
例4 用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
分析:首先要建立适当的平面直角坐标系,用坐标表示有关的量,然后进行代数运算,最后把代数运算的结果 “翻译”成几何关系.
补充练习
如图所示,已知BD是△ABC的边AC上的中线,建立适当的平面直角坐标系,证明:|AB|2+|BC|2- |AC|2=2|BD|2.
证明 如图所示,以AC所在的直线为x轴,点D为坐标原点,建立平面直角坐标系.设B(b,c),C(a,0),依题意得A(-a,0).
思考
在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题.你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
上述利用“坐标法”解决平面几何问题的基本步骤可以概括为
课堂小结
举一反三
举一反三
函数的最小值是______
解:设A(-1,2),B(3,1),P(x,0),
则f(x)表示点P(x,0)到点A(-1,2),B(3,1)两点的距离之和,
即|PA|+|PB|,
点P是x轴上的点,则点A关于x轴的对称点A`(-1,-2),
所以|PA|=|PA`|,
所以|PA|+|PB|=|PA`|+|PB|≥|AB|=,
所以f(x)的最小值是5.
y
x
P
B
A
A’
O
5
复习回顾
平面内两点P1(x1,y1),P2(x2,y2),
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
P到直线 l 的距离,即垂线段|PQ|的长度
可以验证,当A=0,或B=0时,上述公式仍然成立.
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
追问:求点P到直线 l 的距离你还有什么方法?
我们知道,向量是解决距离、角度问题的有力工具,能否用向量方法求点到直线的距离?
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
追问:求点P到直线 l 的距离你还有什么方法?
合作探究
因此,点到直线 l :Ax + By + C=0的距离
①运用此公式时要注意直线方程必须是一般式,若给出其他形式,应先化成一般式再用公式;
②分母是直线未知数x, y系数平方和的算术跟;
③分子是P点代入直线方程;
④直线方程 Ax +By + C=0中,A=0或B=0公式也成立。但由于直线是特殊直线(与坐标轴垂直),故也可以用数形结合求解.
例1求点P(-1,2)到直线l:3x=2的距离.
方法1.
方法2.解点P(-1,2)到直线l:x=的距离.
例2.已知ΔABC的三个顶点A(1,3),B(3,1),C(-1,0),求ΔABC的面积.
x
y
O
A
C
B
(2)法一:把方程y=6写成0·x+y-6=0,由点到直线的距离公式得d=8.
法二:因为直线y=6平行于x轴,所以d=|6-(-2)|=8.
(3)因为直线x=4平行于y轴,所以d=|4-3|=1.
练习2.已知点A(a,6)到直线3x-4y=2的距离d=4,求a的值.
1.掌握了点到直线的距离公式。
d=
2.能够利用点到直线的距离公式求解有关问题
课堂小结
第二章 直线和圆的方程
2.3.1 两条直线的交点坐标
几何元素及关系 代数表示
点A
直线l
点A在直线l上
(形)
(数)
A (x0,y0)
l:Ax+By+C=0
Ax0 +By0 +C=0
【问题1】点与直线的关系是什么?
A (x0,y0)
Ax+By+C=0
【问题2】在同一直角坐标系内画出直线l1与l2的图象:
l1:3x+4y-2=0;
【追问1】两条直线l1与l2 的位置关系是怎样的?
【追问2】它们的交点坐标与两条直线的方程有什么关系?
【追问3】你能求出交点的坐标吗?
l2
l1
A
(-2,2)
联立方程组:
①
②
l2:2x+y+2=0.
l1:3x+4y-2=0;
l2:2x+y+2=0.
【问题3】上述结论有一般性吗?
若两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0相交,它们的交点坐标与直线的方程有什么关系?由此能得出求其交点坐标的方法吗?
直线l1和l2相交
直线l1和l2存在唯一交点, 记为A(x0,y0)
点A(x0,y0)既在l1上,又在l2上
【问题3】上述结论有一般性吗?
若两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0相交,
它们的交点坐标与直线的方程有什么关系?由此能得出求其
交点坐标的方法吗?
几何元素及关系(形) 代数表示(数)
直线l1与l2的交点是A(x0,y0)
方程组
的唯一解是
l2
l1
【问题4】已知两条直线:l1:4x+2y-3=0;l2:2x+y+2=0,则这两条直线的位置关系是什么?
【追问】能否判断对应方程组解的情况?
没有公共点
方程组无解
不存在点同时满足两条直线方程
l1 ∥ l2
方程组无解
l1 ∥ l2
【问题5】已知两条直线:l1:4x+2y+4=0;l2:2x+y+2=0,则这两条直线的位置关系是什么?
l2
l1
有无数个公共点
存在无数个点同时满足两条直线方程
方程组有无数组解
直线l1和l2重合
方程组有无数组解
l1 和 l2重合
【问题6】一般地,对于两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0 ,你能说出这两条直线的位置关系与对应方程组 的解之间的联系吗?
直线的位置关系 公共点的个数 方程组解的个数 图 例
相 交
平 行
重 合
有且仅有1个
唯一解
0 个
无 解
无数个
无数组解
【问题7】(1) l1:3x+4y-2=0,l2:2x+y+2=0
(2) l1:4x+2y+3=0,l2:2x+y+2=0
(3) l1:4x+2y+4=0,l2:2x+y+2=0
对于以上三组直线,你还有其他方法判断每组直线间的位置关系么?
【追问1】能否用斜率判断两条直线的位置关系?
两直线斜率均不存在
垂直于 x 轴
截距相等重合
截距不等平行
一条斜率不存在
一条斜率存在
两直线斜率均存在
斜率不等相交
斜率相等看截距
截距相等重合
截距不等平行
两条直线相交
【问题7】(1) l1:3x+4y-2=0,l2:2x+y+2=0
(2) l1:4x+2y+3=0,l2:2x+y+2=0
(3) l1:4x+2y+4=0,l2:2x+y+2=0
对于以上三组直线,你还有其他方法判断每组直线间的位置关系么?
【追问2】如何从直线方程的一般式中确定斜率?
l1:yl2:y
k1≠k2
相交
l1:yl2:y
k1=k2b1≠b2
平行
l1:yl2:y
k1=k2b1=b2
重合
斜截式
【问题8】比较用斜率判断和解方程组判断两直线位置关系,你有什么体会?
代数方法
关注直线方程系数关系,快速判断两条直线平行、重合或相交(垂直).
解方程组判断
斜率判断
关注解的个数与交点个数的对应,判断两条直线平行、重合或相交;
求相交直线的交点坐标.
【问题9】判断两条直线的位置关系,直线方程的系数需要满足怎样的特征?
两直线位置关系 方程系数特征
相交
平行
重合
【例1】 判断下列各对直线的位置关系.如果相交,求出交点的坐标.
(1) l1:x-y=0;l2:3x+3y-10=0.
(2) l1:3x-y +4=0;l2:6x-2y-1=0.
(3) l1:3x+4 y-5=0;l2:6x+8y-10=0.
【例2】求经过直线3x-2y+1=0和直线x+3y+4=0的交点,并且平行于
直线x-y+4=0的直线方程.
【追问1】求解直线方程需要具备哪些条件?
【追问2】分析本题中的条件,可以获得哪些确定直线的信息?
交点坐标(-1,-1)
因为所求直线与xy+4=0平行,故直线的斜率为k=1
设直线方程为:y (1)=x (1),
整理得: x
解:
【问题10】方程3x+4y-2+λ(2x+y+2)=0,当λ变化时表示什么图形?该图形有何特点?
令λ=0,方程化为3x+4y-2=0,此时的图形是一条直线;
令λ=1,得到5x+5y=0,也是一条直线,(-2,2);
令λ= - 1,则x+3y-4=0,还是一条直线, (-2,2).
……
猜想:
当λ变化时,方程表示的是相交于点(-2,2)的直线
(-2,2)
(-2,2)
(-2,2)
【问题10】方程3x+4y-2+λ(2x+y+2)=0,当λ变化时表示什么图形?该图形有何特点?
(3+2λ)x+(4+λ)y+2λ-2=0
Ax+By+C=0
直线
3x+4y-2+λ(2x+y+2)=0
联立方程组:
解得交点坐标为(-2,2).
(3+2λ)x+(4+λ)y+2λ-2=0
λ
无解
经过两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0交点的直线系方程可以表示为:
A1x+B1y +C1 +λ(A2x+B2y +C2 )=0
求相交直线交点坐标
判断两条直线的位置关系
(相交、平行、重合)
解方程组
思想方法
数形结合
特殊到一般
问题导入
问题1:如下图已知平面内两点P1(x1,y1), P2(x2,y2) ,如何求P1, P2间的距离?
y
x
o
P2
P1
特别地, 原点O(0, 0)与任一点P(x, y)间的距离为:
求|P1P2|转化为求向量的模:
问题导入
k是直线P1P2的斜率则两点间距离公式有如下变形:
(1)当P1P2与x轴平行或重合时,
(2)当P1P2与y轴平行或重合时,
问题2:还有其它推导两点间的距离公式的方法吗?
问题导入
|P1P2|=|x2-x1|;
|P1P2|=|y2-y1|;
问题导入
问题2:还有其它推导两点间的距离公式的方法吗?
如右图,我们以P1P2为斜边构造一个直角三角形1P2Q,则点Q的坐标为(),
由勾股定理得:
∴平面内两点P1(x1, y1), P2(x2, y2)间的距离公式为:
一般选择与坐标轴平行(或垂直)的直线构造直角三角形(相应的长度易用坐标表示。)
(3)当P1P2与轴、y轴都不平行时
思考:在推导两点间距离公式时,勾股定理法与向量法比较,你有什么体会?
问题导入
用勾股定理推导平面上两点间的距离公式,不仅需要分情况讨论,还需要添加辅助线构造直角三角形,而向量法比用勾股定理推导方法简洁.
课堂练习P74
典型例题
例3 已知点A(-1,2),B(2, ),在轴上求一点P,使|PA|=|PB|,并求|PA|的值.
一题多解
例3 已知点A(-1,2),B(2, ),在轴上求一点P,使|PA|=|PB|,并求|PA|的值.
这个题目还有其他解法吗?看到 “|PA|=|PB|”,你想到了什么?
点P可以看成是线段AB的垂直平分线与轴的交点!
课堂练习P79
典型例题
例4 用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
分析:首先要建立适当的平面直角坐标系,用坐标表示有关的量,然后进行代数运算,最后把代数运算的结果 “翻译”成几何关系.
补充练习
如图所示,已知BD是△ABC的边AC上的中线,建立适当的平面直角坐标系,证明:|AB|2+|BC|2- |AC|2=2|BD|2.
证明 如图所示,以AC所在的直线为x轴,点D为坐标原点,建立平面直角坐标系.设B(b,c),C(a,0),依题意得A(-a,0).
思考
在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题.你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
上述利用“坐标法”解决平面几何问题的基本步骤可以概括为
课堂小结
举一反三
举一反三
函数的最小值是______
解:设A(-1,2),B(3,1),P(x,0),
则f(x)表示点P(x,0)到点A(-1,2),B(3,1)两点的距离之和,
即|PA|+|PB|,
点P是x轴上的点,则点A关于x轴的对称点A`(-1,-2),
所以|PA|=|PA`|,
所以|PA|+|PB|=|PA`|+|PB|≥|AB|=,
所以f(x)的最小值是5.
y
x
P
B
A
A’
O
5
复习回顾
平面内两点P1(x1,y1),P2(x2,y2),
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
P到直线 l 的距离,即垂线段|PQ|的长度
可以验证,当A=0,或B=0时,上述公式仍然成立.
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
追问:求点P到直线 l 的距离你还有什么方法?
我们知道,向量是解决距离、角度问题的有力工具,能否用向量方法求点到直线的距离?
问题1.如图,已知点P(x0,y0),直线l:Ax+By+C=0,如何求点P到直线 l 的距离?
x
y
O
P
Q
l
追问:求点P到直线 l 的距离你还有什么方法?
合作探究
因此,点到直线 l :Ax + By + C=0的距离
①运用此公式时要注意直线方程必须是一般式,若给出其他形式,应先化成一般式再用公式;
②分母是直线未知数x, y系数平方和的算术跟;
③分子是P点代入直线方程;
④直线方程 Ax +By + C=0中,A=0或B=0公式也成立。但由于直线是特殊直线(与坐标轴垂直),故也可以用数形结合求解.
例1求点P(-1,2)到直线l:3x=2的距离.
方法1.
方法2.解点P(-1,2)到直线l:x=的距离.
例2.已知ΔABC的三个顶点A(1,3),B(3,1),C(-1,0),求ΔABC的面积.
x
y
O
A
C
B
(2)法一:把方程y=6写成0·x+y-6=0,由点到直线的距离公式得d=8.
法二:因为直线y=6平行于x轴,所以d=|6-(-2)|=8.
(3)因为直线x=4平行于y轴,所以d=|4-3|=1.
练习2.已知点A(a,6)到直线3x-4y=2的距离d=4,求a的值.
1.掌握了点到直线的距离公式。
d=
2.能够利用点到直线的距离公式求解有关问题
课堂小结
