08临考资料高考数学解析几何综合题命题分析及解题思路分析(浙江省宁波市)
文档属性
| 名称 | 08临考资料高考数学解析几何综合题命题分析及解题思路分析(浙江省宁波市) | 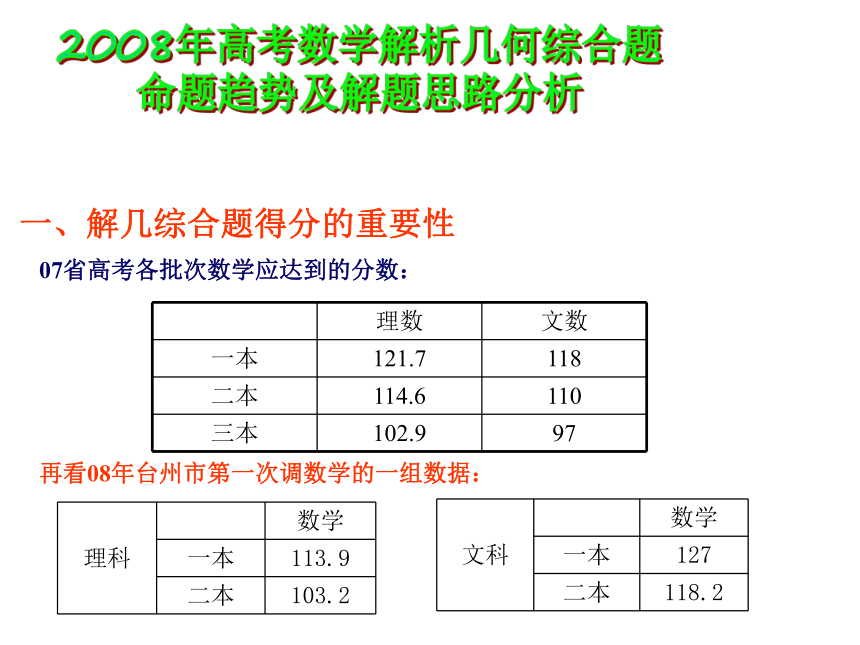 | |
| 格式 | rar | ||
| 文件大小 | 140.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-30 08:56:00 | ||
图片预览



文档简介
课件11张PPT。一、解几综合题得分的重要性07省高考各批次数学应达到的分数:再看08年台州市第一次调数学的一组数据:2008年高考数学解析几何综合题
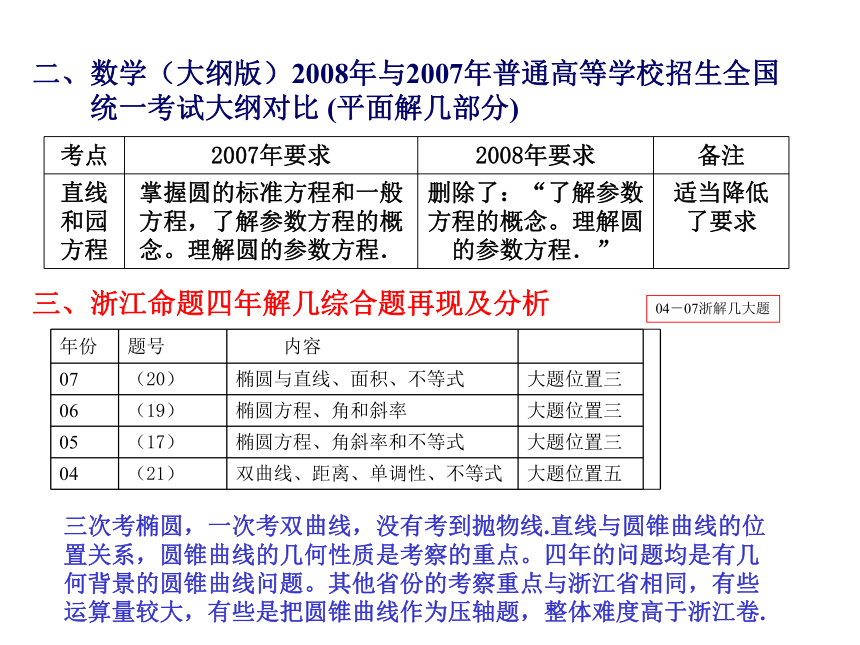
命题趋势及解题思路分析 二、数学(大纲版)2008年与2007年普通高等学校招生全国
统一考试大纲对比 (平面解几部分)三、浙江命题四年解几综合题再现及分析三次考椭圆,一次考双曲线,没有考到抛物线.直线与圆锥曲线的位
置关系,圆锥曲线的几何性质是考察的重点。四年的问题均是有几
何背景的圆锥曲线问题。其他省份的考察重点与浙江省相同,有些
运算量较大,有些是把圆锥曲线作为压轴题,整体难度高于浙江卷.04-07浙解几大题解几综合题得分不理想,其原因主要体现在以下几个方面:
(从全国各地的考卷看)(1)解析几何是代数与几何的完美结合,解析几何的问题可以涉及
函数、方程、不等式、三角、几何、数列、向量等知识,形成
了轨迹、最值、对称、范围、参系数等多种问题,因而成为高
中数学综合能力要求最高的内容之一.(2)解析几何的计算量相对偏大.四、解几综合题常见类型及解题思路案例分析(1)直线与圆锥曲线的位置关系(含各种对称、切线)的研究与讨论仍然是重中之重. 由于导数的介入,抛物线的切线问题将有可能进一步“升温”.直线和圆锥曲线位置关系问题是解析几何问题大题的难点问题,通常学生在
解决直线和圆锥曲线问题上,往往要做三步,一就是联立方程组,二就是求
判别式,并且判别符号..第三,运用韦达定理,如果这三步做完了,就是解
不等式,或者求函数的值域或定义域的问题了. 具体请看:类似题有江苏07理倒数第3题(06天津理22难题)如图,以椭圆的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭 右焦点F(c,0) ( )作垂直于x轴的直线象限内的点A.连结OA交小圆于点B.设直线BF是小圆的切线.,并求直线与y轴的交点M的坐标;
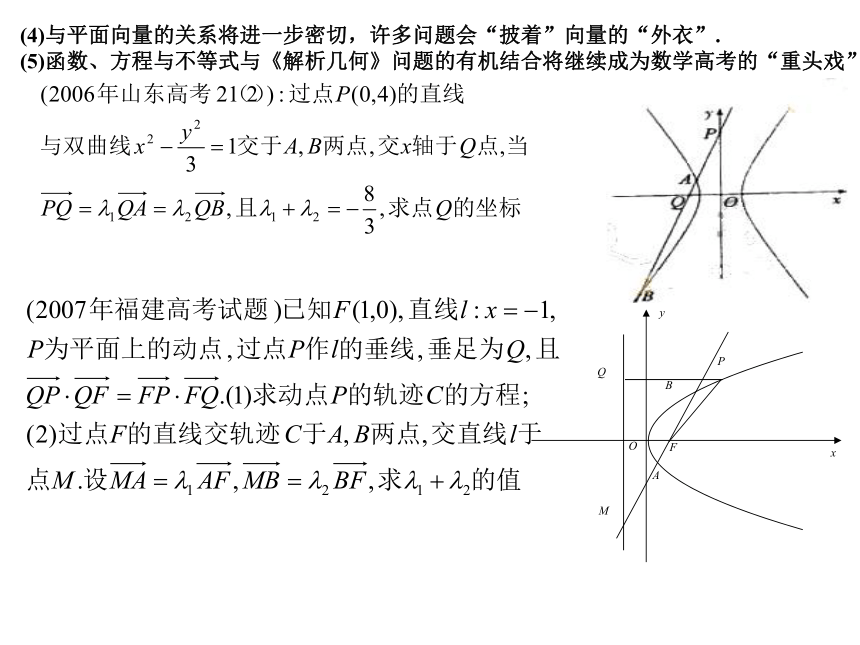
(2)设直线BF交椭圆于P、Q两点,证明 交大圆于第一(1)证明(3)抛物线、椭圆与双曲线之间关系的研究与讨论也将有所体现.(4)与平面向量的关系将进一步密切,许多问题会“披着”向量的“外衣”. (5)函数、方程与不等式与《解析几何》问题的有机结合将继续成为数学高考的“重头戏”.(6)有几何背景的圆锥曲线问题一直是命题的热点. 已知抛物线过点的直线交抛物线于设轴的对称点则直线必过FPQR . 变式一:过点的直线交抛物线,设点关于轴的对称点则直线必过抛物线的焦点.变式二:过点的直线交抛物线与抛物线交于另一点则变式三:已知抛物线两点,设点关于轴的对称点为,则直线RQ必过定点变式四:已知椭圆,过的直线交椭圆C于,设变式五:把(4)中的椭圆方程换成双曲线,有同样的结论. 并与抛物线交于求证直线(1)已知双曲线的方程是. 设斜率为的直线交双曲线于两点,的中点为. 证明:当直线平行移动时,动点(2)利用(1)所揭示的双曲线几何性质,用作图方法找出下面给定双曲
线的中心,简要写出作图步骤,并在图中标出双曲线的中心.在一条过原点的定直线上;(7)数列与《解析几何》问题的携手是一种值得关注的动向.(8)《平面几何》的知识在解决《解析几何》问题的作用不可忽视.重点题型要熟练掌握,如:(1)中点弦问题
具有斜率的弦中点问题,常用设而不求法(点差法):设曲线上两点为 代入方程,然后两方程相减,再应用中点关系及斜率公式,消去四个参数.(2)焦点三角形问题
椭圆或双曲线上一点,与两个焦点构成的三角形问题,常用正、余弦定理搭桥.(3)直线与圆锥曲线位置关系问题
直线与圆锥曲线的位置关系的基本方法是解方程组,进而转化为一元二次方程后利用判别式,应特别注意数
形结合的办法(4)圆锥曲线的有关最值(范围)问题
圆锥曲线中的有关最值(范围)问题,常用代数法和几何法解决
<1>若命题的条件和结论具有明显的几何意义,一般可用图形性质来解决;
<2>若命题的条件和结论体现明确的函数关系式,则可建立目标函数(通常利用二次函数,三角函数,均值不
等式)求最值(5)求曲线的方程问题
<1>曲线的形状已知--------这类问题一般可用待定系数法解决; <2>曲线的形状未知-----求轨迹方程(6) 存在两点关于直线对称问题
在曲线上两点关于某直线对称问题,可以按如下方式分三步解决:求两点所在的直线,求这两直线的交点,使这交点在圆锥曲线形内(当然也可以利用韦达定理并结合判别式来解决)重点题型举例 求曲线方程、求弦长、求角、求面积、求特征量、求最值、证明某种关系、
证明定值、求轨迹、求参数的取值范围、探索型、存在性讨论等问题仍将是
常见的问题.(06辽宁20)已知点 ,是抛物线上的两个动点,O是坐标原点,向量,满足设圆的方程为
(1) 证明线段AB是圆C的直径;(2)当圆C的圆心到直线 的距离的最小值 为时,求P的值.Thank You !结束语:
“问渠哪得清如许,为有源头活水来”。纵观各式各样的高考题,试题越来越“返璞归真 ”,既不需要深奥的知识,也没有高难的技巧,许多题目扎根于课本,由若干基础知识经串联、加工、改造而成,因此在高三复习时要抓住主干知识进行强化复习,重视典例分析,通过引申、拓展、探究,做到解一题通一片,跳出题海,提高复习的实效性。
命题趋势及解题思路分析 二、数学(大纲版)2008年与2007年普通高等学校招生全国
统一考试大纲对比 (平面解几部分)三、浙江命题四年解几综合题再现及分析三次考椭圆,一次考双曲线,没有考到抛物线.直线与圆锥曲线的位
置关系,圆锥曲线的几何性质是考察的重点。四年的问题均是有几
何背景的圆锥曲线问题。其他省份的考察重点与浙江省相同,有些
运算量较大,有些是把圆锥曲线作为压轴题,整体难度高于浙江卷.04-07浙解几大题解几综合题得分不理想,其原因主要体现在以下几个方面:
(从全国各地的考卷看)(1)解析几何是代数与几何的完美结合,解析几何的问题可以涉及
函数、方程、不等式、三角、几何、数列、向量等知识,形成
了轨迹、最值、对称、范围、参系数等多种问题,因而成为高
中数学综合能力要求最高的内容之一.(2)解析几何的计算量相对偏大.四、解几综合题常见类型及解题思路案例分析(1)直线与圆锥曲线的位置关系(含各种对称、切线)的研究与讨论仍然是重中之重. 由于导数的介入,抛物线的切线问题将有可能进一步“升温”.直线和圆锥曲线位置关系问题是解析几何问题大题的难点问题,通常学生在
解决直线和圆锥曲线问题上,往往要做三步,一就是联立方程组,二就是求
判别式,并且判别符号..第三,运用韦达定理,如果这三步做完了,就是解
不等式,或者求函数的值域或定义域的问题了. 具体请看:类似题有江苏07理倒数第3题(06天津理22难题)如图,以椭圆的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭 右焦点F(c,0) ( )作垂直于x轴的直线象限内的点A.连结OA交小圆于点B.设直线BF是小圆的切线.,并求直线与y轴的交点M的坐标;
(2)设直线BF交椭圆于P、Q两点,证明 交大圆于第一(1)证明(3)抛物线、椭圆与双曲线之间关系的研究与讨论也将有所体现.(4)与平面向量的关系将进一步密切,许多问题会“披着”向量的“外衣”. (5)函数、方程与不等式与《解析几何》问题的有机结合将继续成为数学高考的“重头戏”.(6)有几何背景的圆锥曲线问题一直是命题的热点. 已知抛物线过点的直线交抛物线于设轴的对称点则直线必过FPQR . 变式一:过点的直线交抛物线,设点关于轴的对称点则直线必过抛物线的焦点.变式二:过点的直线交抛物线与抛物线交于另一点则变式三:已知抛物线两点,设点关于轴的对称点为,则直线RQ必过定点变式四:已知椭圆,过的直线交椭圆C于,设变式五:把(4)中的椭圆方程换成双曲线,有同样的结论. 并与抛物线交于求证直线(1)已知双曲线的方程是. 设斜率为的直线交双曲线于两点,的中点为. 证明:当直线平行移动时,动点(2)利用(1)所揭示的双曲线几何性质,用作图方法找出下面给定双曲
线的中心,简要写出作图步骤,并在图中标出双曲线的中心.在一条过原点的定直线上;(7)数列与《解析几何》问题的携手是一种值得关注的动向.(8)《平面几何》的知识在解决《解析几何》问题的作用不可忽视.重点题型要熟练掌握,如:(1)中点弦问题
具有斜率的弦中点问题,常用设而不求法(点差法):设曲线上两点为 代入方程,然后两方程相减,再应用中点关系及斜率公式,消去四个参数.(2)焦点三角形问题
椭圆或双曲线上一点,与两个焦点构成的三角形问题,常用正、余弦定理搭桥.(3)直线与圆锥曲线位置关系问题
直线与圆锥曲线的位置关系的基本方法是解方程组,进而转化为一元二次方程后利用判别式,应特别注意数
形结合的办法(4)圆锥曲线的有关最值(范围)问题
圆锥曲线中的有关最值(范围)问题,常用代数法和几何法解决
<1>若命题的条件和结论具有明显的几何意义,一般可用图形性质来解决;
<2>若命题的条件和结论体现明确的函数关系式,则可建立目标函数(通常利用二次函数,三角函数,均值不
等式)求最值(5)求曲线的方程问题
<1>曲线的形状已知--------这类问题一般可用待定系数法解决; <2>曲线的形状未知-----求轨迹方程(6) 存在两点关于直线对称问题
在曲线上两点关于某直线对称问题,可以按如下方式分三步解决:求两点所在的直线,求这两直线的交点,使这交点在圆锥曲线形内(当然也可以利用韦达定理并结合判别式来解决)重点题型举例 求曲线方程、求弦长、求角、求面积、求特征量、求最值、证明某种关系、
证明定值、求轨迹、求参数的取值范围、探索型、存在性讨论等问题仍将是
常见的问题.(06辽宁20)已知点 ,是抛物线上的两个动点,O是坐标原点,向量,满足设圆的方程为
(1) 证明线段AB是圆C的直径;(2)当圆C的圆心到直线 的距离的最小值 为时,求P的值.Thank You !结束语:
“问渠哪得清如许,为有源头活水来”。纵观各式各样的高考题,试题越来越“返璞归真 ”,既不需要深奥的知识,也没有高难的技巧,许多题目扎根于课本,由若干基础知识经串联、加工、改造而成,因此在高三复习时要抓住主干知识进行强化复习,重视典例分析,通过引申、拓展、探究,做到解一题通一片,跳出题海,提高复习的实效性。
同课章节目录
