青岛版数学九年级上册4.2 用配方法解一元二次方程直接开平方法 说课课件(共25张PPT)
文档属性
| 名称 | 青岛版数学九年级上册4.2 用配方法解一元二次方程直接开平方法 说课课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 21:59:43 | ||
图片预览







文档简介
(共25张PPT)
4.2 用配方法解一元二次方程
直接开平方法说课
说 得 失
流 程
说 模 式
说 教 材
说 设 计
直接开平方法
说 得 失
流 程
说 模 式
说 教 材
说 设 计
勾股定理说课
直接开平方法
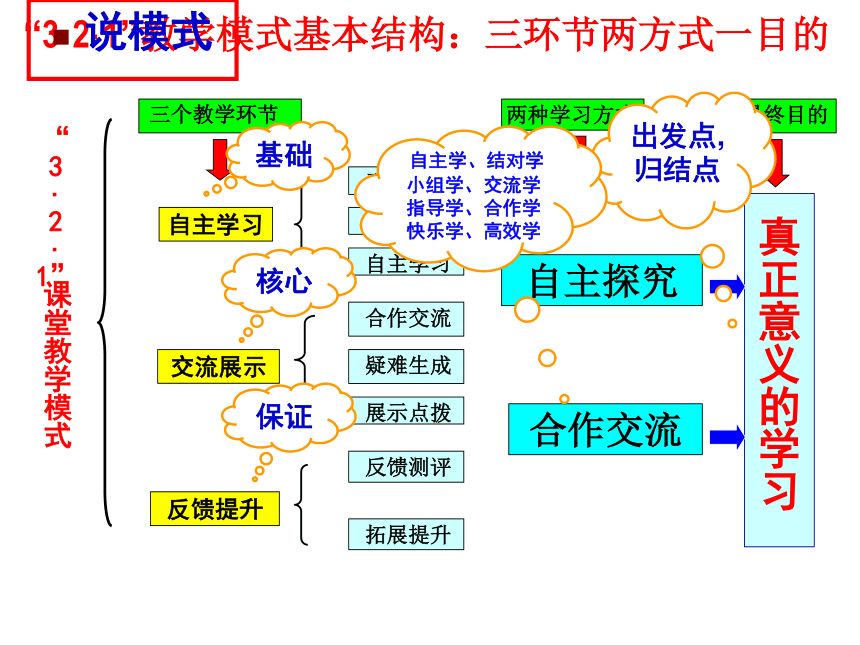
“3·2·1”教学模式基本结构:三环节两方式一目的
课堂教学模式
三个教学环节
两种学习方式
一个最终目的
自主学习
交流展示
反馈提升
引入定向
自学指导
自主学习
合作交流
疑难生成
展示点拨
反馈测评
拓展提升
自主探究
合作交流
真正意义的学习
基础
核心
保证
“3
·
2
·
1”
出发点,
归结点
说模式
自主学、结对学
小组学、交流学
指导学、合作学
快乐学、高效学
课改课堂的10大特征
1.面向全体学生 2.以学生为主体
3.以教师为主导 4.体现民主平等
5.落实开放课堂 6.运用分组教学
7.有效的自主合作探究 8.教材校本化改造
9. 与实践充分接轨 10.快节奏、高效率、大容量
自主学习
快速阅读、读出问题、标划记录、查找疑难、强化记忆;
合作交流
合理分工、表述质疑、指导讲解、倾听演练、疑难共商;
展示拓展
规范板书、研讨疑难、讲解展示、补充抢答、倾听记录。
学生课堂行为的15个标准
“三策略一转型”
训练前置
学案作业一体化
三色学案
作业转型
落实课堂高效和减负
“三为主”课堂推进策略
通过实践,我校总结出了符合我校特点的“三为主”课堂推进策略:即以教材为主源,以导学案为主线,以解决问题和疑难为主攻。
应处理好的十大关系
1.自主探究与合作学习。2.静态高效与动态课堂。
3.继承发扬与改革创新。4.教师主导与学生主体。
5.教材使用与拓展延伸。6.理念贯彻与现代手段。
7.课程理念与学科特点。8.考试成绩与综合素质。
9.学习时间与学习效率。10.刻苦学习与教育幸福。
应避免的十大误区
1. 课改操作模式化,缺乏灵活创新。
2.讨论、展示形式化,活动层次低。
3.学生讨论不出的问题,也要学生讨论。
4.将黑板学生板演作为课改的唯一特征。
5.将教师一言堂变为学生一言堂。
6.学生预习、讨论、展示习惯不到位。
7.课堂与学案两张皮。
8.不能有效的将学科特点与课改有效结合。
9.严格按所有组分任务,展示时间过长。
10.预习完全放在课下,导致学生应付学案,不真正预习教材。
特色课堂与灵活课堂
课堂教学模式
三个教学环节
两种学习方式
一个最终目的
自主学习
交流展示
反馈提升
引入定向
自学指导
自主学习
合作交流
疑难生成
展示点拨
反馈测评
拓展提升
自主探究
合作交流
真正意义的学习
打造一种以课改理念为指导,以学生为主体,教师为主导,以小组活动和课堂展示为载体的新型课堂
流程可以删减、颠倒、循环或有所侧重,给予不同学科和课堂更大的开放空间。学生在课堂上要遵循的行为标准必须落实到位,课改课堂也必须体现十大特征,处理好十大关系,避免十大误区 ,从而打破固定的模式。
“3
·
2
·
1”
说 得 失
流 程
说 模 式
说 教 材
说 设 计
勾股定理说课
直接开平方法
说教材——说课标
什么是直接开平方法
直接开平方法的应用
知道形如x 2=b (b≥0) 或(x+a) 2=b(b≥0)的一元二次方程可以用直接开平方法求解;
直接开平方法
主要内容
知道直接开平方法求一元二次方程的解的依据是数的开平方;
能够熟练而准确的运用直接开平方法求一元二次方程的解。
对圆的进一步认识
主要内容
图形与变换
一元二次方程
九年级上册
特殊四边形
说教材——说单元
一元二次方程是“数与代数”领域的重要内容,是继已经学过的一元一次方程、二元一次方程组和可化为一元一次方程的分式方程之后,对方程研究的继续,也是下学期学习二次函数的基础,因此,本章内容在初中数学知识体系中具有承上启下的重要地位。
直接开平方法
说 得 失
流 程
说 教 材
说 模 式
说 设 计
新课导入、明确目标
自主探索、合作交流
挑战自我、拓展提高
回顾反思、提炼精华
达标检测、当堂反馈
莘县实验初中的教学模式
数学学科特色教学模式
4.2 用配方法解一元二次方程
(第1课时)
城南有一块边长为15米的正方形绿地,需扩大绿化面积,预计规划后的正方形绿地面积将达到300平方米,请问这块绿地的边长增加了多少米?(结果保留一位小数)
情境导入,明确目标
学习目标:
1、知道形如x 2=b (b≥0) 或(x+a) 2=b(b≥0)的一元二次方程可以用直接开平方法求解;
2、知道直接开平方法求一元二次方程的解的依据是数的开平方;
3、能够熟练而准确的运用直接开平方法求一元二次方程的解。
激发学习兴趣
引发学生思考
明确学习目标,做到心中有数
合作学习 共同回顾
一个数x的平方等于a,这个数x叫做a的什么?
即 ,则x叫做a的平方根,表示为:
即 (a≥0)则x叫做a的平方根,表示为:
下列各数有平方根吗 若有,你能求出它的平方根吗
回忆平方根的有关知识,为本节课做准备。
教师巡回督导,了解自学情况,进行个别点拨,组织有效交流,注重学生评价,实现最终目的。
独立完成
组内讨论
代表汇报
教师点拨
自主探索,合作交流
解方程:
用直接开平方法解方程:
充分体现了教学模式“两方式”中的“自主探究、合作交流”两种学习方式。
知识归纳,规律总结
用直接开平方法来解的方程有什么特征
直接开平方法可用于以下类型的一元二次方程
注意:负数没有平方根,故b≥0
学以致用,巩固新知
独立思考
代表汇报
教师点拨
下列一元二次方程中,哪些更适宜用直接开平方法来解
⑴ x2=3 ⑵ 3t2-t=0
⑶ 3y2=27 ⑷ (y-1)2-4=0
⑸ 4x2+2=0 ⑹ x2=36x
挑战自我,拓展提高
学生讲解展示,教师强调。
独立思考
小组交流
代表汇报
教师点拨
1、解方程:x2+6x+9=25
2、若关于x的一元二次方程
的常数项是0,求m的值
1、今天我们主要学习了什么内容?
2、本节课所体现的数学思想是什么?
回顾反思 提炼精华
达标检测 当堂反馈
1.用求平方根的方法解一元二次方程的方法叫__________.
2. 如果x2=121,那么x1=__________,x2=___________.
3. 如果3x2=18那么x1=__________,x2=___________.
4. 如果25x2-16=0那么x1=__________,x2=___________.
5. 如果x2=a(a≥0)那么 x1=__________,x2=___________.
6、用直接开平方法解下列方程:
(x-1) 2=8 2. (2x+3) 2=1
3. ( x+1) 2-4=0
直接开平方法
11
-11
这一过程就是“三环节”中的“反馈提升”环节,最终目的是落实学生“真正意义上的学习”
感谢大家的聆听!
请各位老师多提宝贵意见!
4.2 用配方法解一元二次方程
直接开平方法说课
说 得 失
流 程
说 模 式
说 教 材
说 设 计
直接开平方法
说 得 失
流 程
说 模 式
说 教 材
说 设 计
勾股定理说课
直接开平方法
“3·2·1”教学模式基本结构:三环节两方式一目的
课堂教学模式
三个教学环节
两种学习方式
一个最终目的
自主学习
交流展示
反馈提升
引入定向
自学指导
自主学习
合作交流
疑难生成
展示点拨
反馈测评
拓展提升
自主探究
合作交流
真正意义的学习
基础
核心
保证
“3
·
2
·
1”
出发点,
归结点
说模式
自主学、结对学
小组学、交流学
指导学、合作学
快乐学、高效学
课改课堂的10大特征
1.面向全体学生 2.以学生为主体
3.以教师为主导 4.体现民主平等
5.落实开放课堂 6.运用分组教学
7.有效的自主合作探究 8.教材校本化改造
9. 与实践充分接轨 10.快节奏、高效率、大容量
自主学习
快速阅读、读出问题、标划记录、查找疑难、强化记忆;
合作交流
合理分工、表述质疑、指导讲解、倾听演练、疑难共商;
展示拓展
规范板书、研讨疑难、讲解展示、补充抢答、倾听记录。
学生课堂行为的15个标准
“三策略一转型”
训练前置
学案作业一体化
三色学案
作业转型
落实课堂高效和减负
“三为主”课堂推进策略
通过实践,我校总结出了符合我校特点的“三为主”课堂推进策略:即以教材为主源,以导学案为主线,以解决问题和疑难为主攻。
应处理好的十大关系
1.自主探究与合作学习。2.静态高效与动态课堂。
3.继承发扬与改革创新。4.教师主导与学生主体。
5.教材使用与拓展延伸。6.理念贯彻与现代手段。
7.课程理念与学科特点。8.考试成绩与综合素质。
9.学习时间与学习效率。10.刻苦学习与教育幸福。
应避免的十大误区
1. 课改操作模式化,缺乏灵活创新。
2.讨论、展示形式化,活动层次低。
3.学生讨论不出的问题,也要学生讨论。
4.将黑板学生板演作为课改的唯一特征。
5.将教师一言堂变为学生一言堂。
6.学生预习、讨论、展示习惯不到位。
7.课堂与学案两张皮。
8.不能有效的将学科特点与课改有效结合。
9.严格按所有组分任务,展示时间过长。
10.预习完全放在课下,导致学生应付学案,不真正预习教材。
特色课堂与灵活课堂
课堂教学模式
三个教学环节
两种学习方式
一个最终目的
自主学习
交流展示
反馈提升
引入定向
自学指导
自主学习
合作交流
疑难生成
展示点拨
反馈测评
拓展提升
自主探究
合作交流
真正意义的学习
打造一种以课改理念为指导,以学生为主体,教师为主导,以小组活动和课堂展示为载体的新型课堂
流程可以删减、颠倒、循环或有所侧重,给予不同学科和课堂更大的开放空间。学生在课堂上要遵循的行为标准必须落实到位,课改课堂也必须体现十大特征,处理好十大关系,避免十大误区 ,从而打破固定的模式。
“3
·
2
·
1”
说 得 失
流 程
说 模 式
说 教 材
说 设 计
勾股定理说课
直接开平方法
说教材——说课标
什么是直接开平方法
直接开平方法的应用
知道形如x 2=b (b≥0) 或(x+a) 2=b(b≥0)的一元二次方程可以用直接开平方法求解;
直接开平方法
主要内容
知道直接开平方法求一元二次方程的解的依据是数的开平方;
能够熟练而准确的运用直接开平方法求一元二次方程的解。
对圆的进一步认识
主要内容
图形与变换
一元二次方程
九年级上册
特殊四边形
说教材——说单元
一元二次方程是“数与代数”领域的重要内容,是继已经学过的一元一次方程、二元一次方程组和可化为一元一次方程的分式方程之后,对方程研究的继续,也是下学期学习二次函数的基础,因此,本章内容在初中数学知识体系中具有承上启下的重要地位。
直接开平方法
说 得 失
流 程
说 教 材
说 模 式
说 设 计
新课导入、明确目标
自主探索、合作交流
挑战自我、拓展提高
回顾反思、提炼精华
达标检测、当堂反馈
莘县实验初中的教学模式
数学学科特色教学模式
4.2 用配方法解一元二次方程
(第1课时)
城南有一块边长为15米的正方形绿地,需扩大绿化面积,预计规划后的正方形绿地面积将达到300平方米,请问这块绿地的边长增加了多少米?(结果保留一位小数)
情境导入,明确目标
学习目标:
1、知道形如x 2=b (b≥0) 或(x+a) 2=b(b≥0)的一元二次方程可以用直接开平方法求解;
2、知道直接开平方法求一元二次方程的解的依据是数的开平方;
3、能够熟练而准确的运用直接开平方法求一元二次方程的解。
激发学习兴趣
引发学生思考
明确学习目标,做到心中有数
合作学习 共同回顾
一个数x的平方等于a,这个数x叫做a的什么?
即 ,则x叫做a的平方根,表示为:
即 (a≥0)则x叫做a的平方根,表示为:
下列各数有平方根吗 若有,你能求出它的平方根吗
回忆平方根的有关知识,为本节课做准备。
教师巡回督导,了解自学情况,进行个别点拨,组织有效交流,注重学生评价,实现最终目的。
独立完成
组内讨论
代表汇报
教师点拨
自主探索,合作交流
解方程:
用直接开平方法解方程:
充分体现了教学模式“两方式”中的“自主探究、合作交流”两种学习方式。
知识归纳,规律总结
用直接开平方法来解的方程有什么特征
直接开平方法可用于以下类型的一元二次方程
注意:负数没有平方根,故b≥0
学以致用,巩固新知
独立思考
代表汇报
教师点拨
下列一元二次方程中,哪些更适宜用直接开平方法来解
⑴ x2=3 ⑵ 3t2-t=0
⑶ 3y2=27 ⑷ (y-1)2-4=0
⑸ 4x2+2=0 ⑹ x2=36x
挑战自我,拓展提高
学生讲解展示,教师强调。
独立思考
小组交流
代表汇报
教师点拨
1、解方程:x2+6x+9=25
2、若关于x的一元二次方程
的常数项是0,求m的值
1、今天我们主要学习了什么内容?
2、本节课所体现的数学思想是什么?
回顾反思 提炼精华
达标检测 当堂反馈
1.用求平方根的方法解一元二次方程的方法叫__________.
2. 如果x2=121,那么x1=__________,x2=___________.
3. 如果3x2=18那么x1=__________,x2=___________.
4. 如果25x2-16=0那么x1=__________,x2=___________.
5. 如果x2=a(a≥0)那么 x1=__________,x2=___________.
6、用直接开平方法解下列方程:
(x-1) 2=8 2. (2x+3) 2=1
3. ( x+1) 2-4=0
直接开平方法
11
-11
这一过程就是“三环节”中的“反馈提升”环节,最终目的是落实学生“真正意义上的学习”
感谢大家的聆听!
请各位老师多提宝贵意见!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
