5.3.1 平行线的性质课件
图片预览





文档简介
课件28张PPT。5.3.1 平行线的性质
(第1课时)AB 课堂练习:已知直线AB 及其外一点P,画出过点P的AB 的平行线。 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.1.梳理旧知,引出新课结论 平行线的判定问题:
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有
什么关系呢?
内错角,同旁内角之间又有什么关系呢?
两
直
线
平
行1.梳理旧知,引出新课条件结论?两条平行线
被第三条直
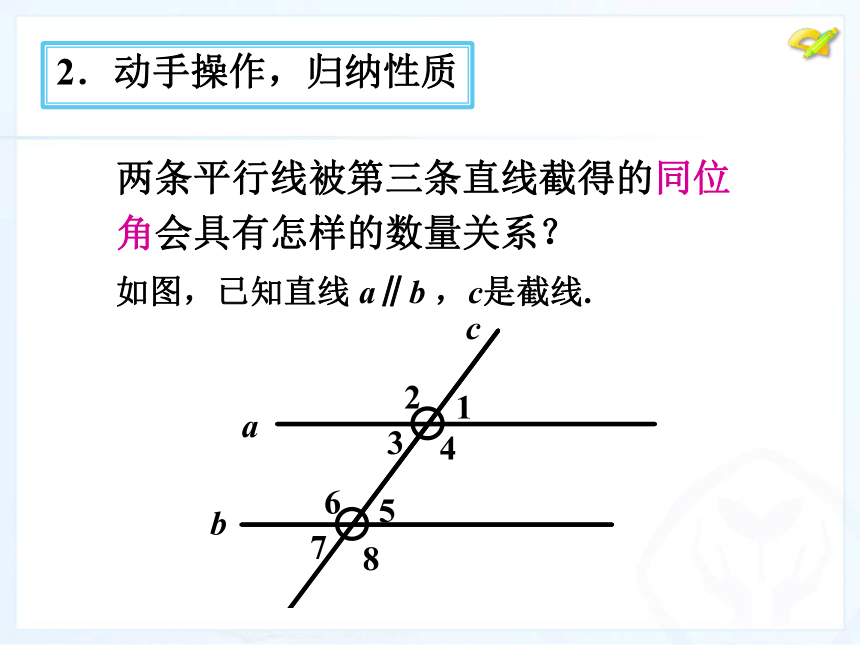
线所截1.梳理旧知,引出新课条件结论同位角?内错角?同旁内角? 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质 如图,已知直线 a∥b ,c是截线. 利用直尺和三角尺画两条平行线a//b,然后,画一条截线c与这两条平行线相交,标出如图的角(图5.3-1)。
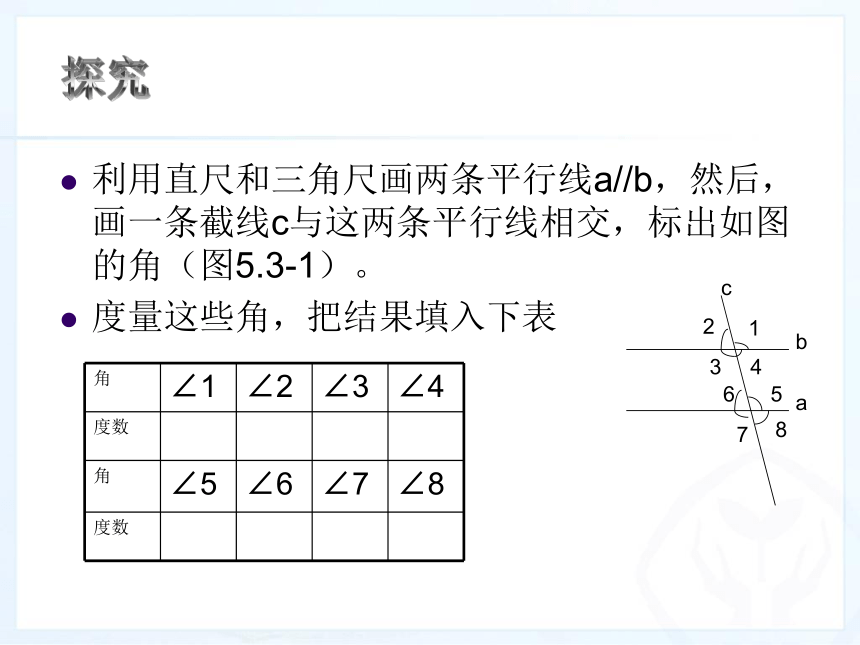
度量这些角,把结果填入下表
abc12345678探究各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想:
两条平行线被第三条直线所截,同位角__,内错角__,同旁内角__。
在任意画一条直线d同样度量并计算各个角的度数,你的猜想还成立吗?
如果直线a与b不平行,你的猜
想还成立吗?abc12345678d 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质性质1 两条平行线被第三条直线 所截,同位角相等. 3.应用转化,推出性质性质2 两条平行线被第三条直线所截,内错角相等.两条平行线被第三条直线截得的内错角会具有怎样的数量关系? 3.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.两条平行线被第三条直线截得的同旁内角会具有怎样的数量关系? 归纳小结一般的平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等。简单说成:两直线平行,同位角相等。
性质2 两条平行线被第三条直线所截,内错角相等。简单说成:两直线平行,内错角相等。
性质3 两条平行线被第三条直线所截,同旁内角互补。简单说成:两直线平行,同旁内角互补。
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”。类似地,你能根据性质1,推出性质2吗?
如图5.3—2
∵a//b
∴∠1=∠2( 两直线平行,同位角相等)
又∵ ∠3= ∠1(对顶角相等)
∴ ∠2= ∠3
对于性质3,你能写出类似的推理过程吗??思考2abc132图5.3—2c? 2?31ba
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
?????练一练:1.如图,AB,CD被EF所截,AB//CD.
按要求填空:若∠1=120°,则∠2=____°( );
∠3=___- ∠1=__°( )123120180°60两直线平行,内错角相等.两直线平行,同旁内角互补.2.如图,已知AB//CD,AD//BC.填空:
(1)∵ AB//CD (已知),
∴ ∠1= ∠___
( );
(2) ∵ AD//BC (已知)
∴ ∠2= ∠___ ( ).两直线平行,内错角相等.两直线平行,内错角相等.DACB3.如图,△ABC的边AB//CE,则:
∠A= ∠__( );
∠B= ∠__( ). 运用刚才的推理,可以说明一个结论,
你想到了吗?思考: 三角形的三个内角和等于180°2两直线平行,内错角相等.1两直线平行,同位角相等.例1: 如图,已知直线a∥b,∠1 = 500,
求∠2的度数.abc12∴∠ 2= 500 (等量代换)解:∵ a∥b(已知)∴∠ 1= ∠ 2
(两直线平行,内错角相等)又∵∠ 1 = 500 (已知)变式1:已知条件不变,求∠3,∠4的度数? 师生互动,典例示范变式2:已知∠3 =∠4,∠1=47°,求∠2的度数?∴∠ 2= 470
( )解:∵ ∠3 =∠4( )∴a∥b
( )
又∵∠ 1 = 470 ( )c1234abd例2 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么? 4.巩固新知,深化理解方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解1方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解2如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?解:∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
即 ∠2=54° ,∠3=126°, ∠4=54°。你会做吗?(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
证:(1)DE∥BC
(2) ∠C的度数同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:(1)平行线的性质是什么?5.归纳小结(2)你能用自己的语言叙述研究平行线性质的过程吗? (3)性质2和性质3是通过简单推理得到的,在推理论证中需要注意哪些问题?图形已知结果结论同位角内错角同旁内角两直线平行
同旁内角互补122324))))))abababccc平行线的性质a//b两直线平行
同位角相等a//b两直线平行
内错角相等a//b教科书 习题5.3 第2、4、6题6.布置作业
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有
什么关系呢?
内错角,同旁内角之间又有什么关系呢?
两
直
线
平
行1.梳理旧知,引出新课条件结论?两条平行线
被第三条直
线所截1.梳理旧知,引出新课条件结论同位角?内错角?同旁内角? 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质 如图,已知直线 a∥b ,c是截线. 利用直尺和三角尺画两条平行线a//b,然后,画一条截线c与这两条平行线相交,标出如图的角(图5.3-1)。
度量这些角,把结果填入下表
abc12345678探究各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想:
两条平行线被第三条直线所截,同位角__,内错角__,同旁内角__。
在任意画一条直线d同样度量并计算各个角的度数,你的猜想还成立吗?
如果直线a与b不平行,你的猜
想还成立吗?abc12345678d 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质性质1 两条平行线被第三条直线 所截,同位角相等. 3.应用转化,推出性质性质2 两条平行线被第三条直线所截,内错角相等.两条平行线被第三条直线截得的内错角会具有怎样的数量关系? 3.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.两条平行线被第三条直线截得的同旁内角会具有怎样的数量关系? 归纳小结一般的平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等。简单说成:两直线平行,同位角相等。
性质2 两条平行线被第三条直线所截,内错角相等。简单说成:两直线平行,内错角相等。
性质3 两条平行线被第三条直线所截,同旁内角互补。简单说成:两直线平行,同旁内角互补。
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”。类似地,你能根据性质1,推出性质2吗?
如图5.3—2
∵a//b
∴∠1=∠2( 两直线平行,同位角相等)
又∵ ∠3= ∠1(对顶角相等)
∴ ∠2= ∠3
对于性质3,你能写出类似的推理过程吗??思考2abc132图5.3—2c? 2?31ba
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
?????练一练:1.如图,AB,CD被EF所截,AB//CD.
按要求填空:若∠1=120°,则∠2=____°( );
∠3=___- ∠1=__°( )123120180°60两直线平行,内错角相等.两直线平行,同旁内角互补.2.如图,已知AB//CD,AD//BC.填空:
(1)∵ AB//CD (已知),
∴ ∠1= ∠___
( );
(2) ∵ AD//BC (已知)
∴ ∠2= ∠___ ( ).两直线平行,内错角相等.两直线平行,内错角相等.DACB3.如图,△ABC的边AB//CE,则:
∠A= ∠__( );
∠B= ∠__( ). 运用刚才的推理,可以说明一个结论,
你想到了吗?思考: 三角形的三个内角和等于180°2两直线平行,内错角相等.1两直线平行,同位角相等.例1: 如图,已知直线a∥b,∠1 = 500,
求∠2的度数.abc12∴∠ 2= 500 (等量代换)解:∵ a∥b(已知)∴∠ 1= ∠ 2
(两直线平行,内错角相等)又∵∠ 1 = 500 (已知)变式1:已知条件不变,求∠3,∠4的度数? 师生互动,典例示范变式2:已知∠3 =∠4,∠1=47°,求∠2的度数?∴∠ 2= 470
( )解:∵ ∠3 =∠4( )∴a∥b
( )
又∵∠ 1 = 470 ( )c1234abd例2 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么? 4.巩固新知,深化理解方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解1方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解2如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?解:∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
即 ∠2=54° ,∠3=126°, ∠4=54°。你会做吗?(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
证:(1)DE∥BC
(2) ∠C的度数同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:(1)平行线的性质是什么?5.归纳小结(2)你能用自己的语言叙述研究平行线性质的过程吗? (3)性质2和性质3是通过简单推理得到的,在推理论证中需要注意哪些问题?图形已知结果结论同位角内错角同旁内角两直线平行
同旁内角互补122324))))))abababccc平行线的性质a//b两直线平行
同位角相等a//b两直线平行
内错角相等a//b教科书 习题5.3 第2、4、6题6.布置作业
