3.4角的分类-四年级数学上册课后作业(含解析)人教版
文档属性
| 名称 | 3.4角的分类-四年级数学上册课后作业(含解析)人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 249.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 14:45:24 | ||
图片预览



文档简介
3.4 角的分类(同步练习)
一、填空题
1 .下图中,已知∠1+∠5 =138°,那么: ∠2 =( )° , ∠3 =( )°。
2 .下图中有( )个直角,有( )个钝角,有( )锐角。
3 .观察下面各个角,把合适的角填入合适的括号中。
锐角有:( ) 钝角有:( )
直角有:( ) 平角有:( )
4.下图中锐角有( )个,直角有( )个,钝角有( )个,平角有( )个。
二、判断题
5 .三个角组成一个平角,这三个角可能都是锐角。 ( )
6 .一个平角减去一个锐角,得到一个钝角.( )
7 .钟面上是 6 时整时,时针和分针所夹的角是平角。 ( )
8 .平角与锐角的差一定是钝角。 ( )
三、选择题
9 .下图中各角关系正确的是( )。
A . ∠ 1 = ∠2 B . ∠3 = ∠4 C . ∠2+∠3 =180°
10 .如图:正方形∠1=( ) °。
A .60° B .45° C .30°
11 . ∠ 1+∠2=平角,已知∠2 是锐角,则∠1 一定是( )
A .锐角 B .直角 C .钝角
12 .把一个平角分成两个角,其中一个是钝角,那么另一角肯定是( )。
A .直角 B .钝角 C .锐角
四、解答题
13.钟面上时针和分针组成的角, 哪一个是直角?哪一个角比直角大?哪一个角比直角
小?
14 .量出下面各角分别是多少度,并在图上标出来。再写出它们各是什么角。
( ) ( ) ( ) ( )
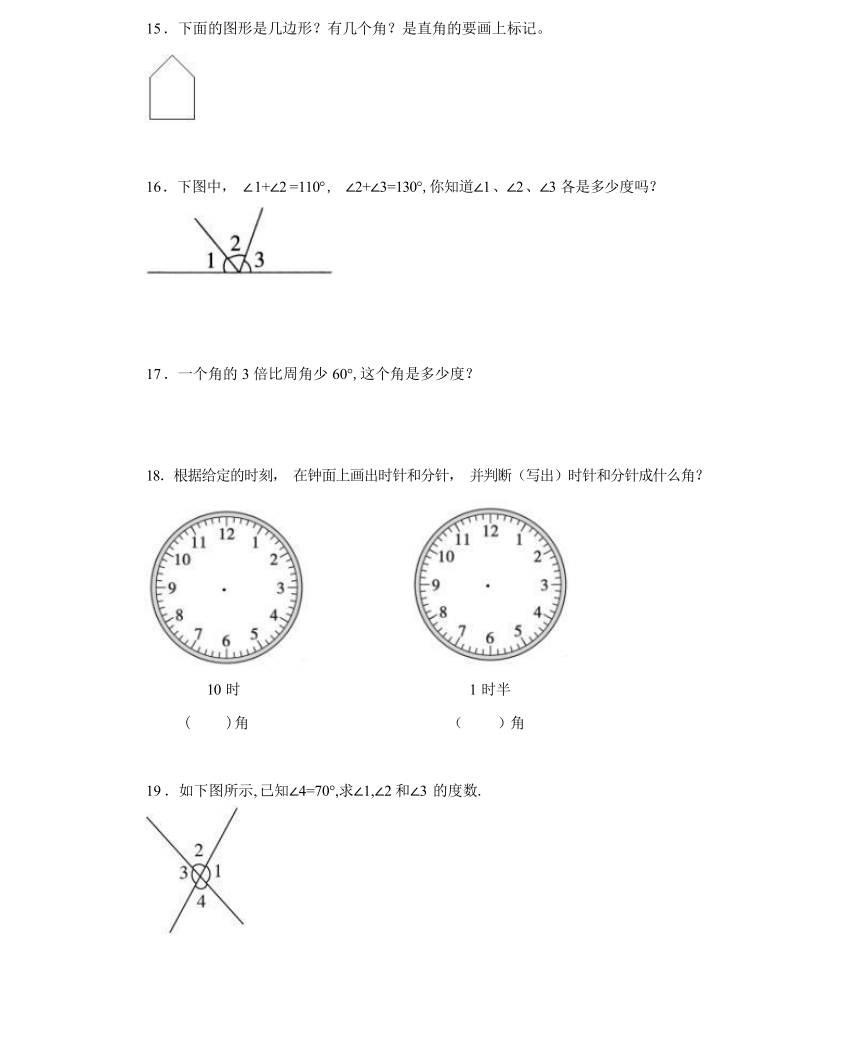
15 .下面的图形是几边形?有几个角?是直角的要画上标记。
16 .下图中, ∠ 1+∠2 =110° , ∠2+∠3=130°,你知道∠1 、∠2 、∠3 各是多少度吗?
17 .一个角的 3 倍比周角少 60°,这个角是多少度?
18.根据给定的时刻, 在钟面上画出时针和分针, 并判断(写出)时针和分针成什么角?
10 时 1 时半
( )角 ( )角
19 .如下图所示, 已知∠4=70°,求∠1,∠2 和∠3 的度数.
1 . 42 138
【分析】∠1+∠5+∠2 等于平角是 180°,让 180°减去 138°就是∠2 的度数; ∠2+∠3 等于平
角是 180°,让 180°减去∠2 的度数即可求解∠3,据此解答。
【详解】因为∠1+∠5+∠2 =180°,所以∠2 =180°-138° =42°
∠2+∠3 =180° , ∠3 =180°-42° = 138°
【点睛】本题考查角的分类和计算,掌握平角是 180 度是解题的关键。
2 . 1 1 4
3 . ∠2 ,∠4 ,∠8 ,∠ 12 ∠3 ,∠7 ,∠9 ,∠ 11 ∠ 1 ,∠5 ,∠ 10 ∠6
4 . 10 4 2 4
【分析】根据长方形的特征,每个角都是直角,根据角的分类, 0°<锐角<90°,直角=
90° , 90°<钝角<180°,平角=180°;据此解答。
【详解】锐角有 10 个:∠DAC 、∠CAB 、∠ABD 、∠DBC 、∠BCA 、∠ACD 、∠CDB 、∠BDA、
∠AOD 、∠BOC;直角有 4 个: ∠ABC 、∠BCD 、∠ADC 、∠BAD;钝角有 2 个: ∠AOB、
∠COD;平角有 4 个: ∠AOC 、∠BOD 、∠COA 、∠DOB。
【点睛】本题考查角的分类,关键注意在数角过程中不要漏数。
5 . √
【分析】小于 90°的角是锐角, 等于 90°的角是直角, 大于 90°小于 180°的角是钝角, 等于 180°
的角是平角,依此判断即可。
【详解】90°+30°+60° = 180°,此时 1 个直角、 2 个锐角组成一个平角。
80°+60°+40° = 180°,此时 3 个锐角组成一个平角。
100°+50°+30° = 180°,此时 1 个钝角、 2 个锐角组成一个平角。
故答案为: √
【点睛】熟练掌握角的分类标准,是解答此题的关键。
6 . √
7 . √
8 . √
【分析】平角是 180°的角, 锐角是小于 90°的角, 平角与锐角的差是大于 90°小于 180°。而
大于 90°小于 180°的角是钝角。据此判断。
【详解】根据分析可知,平角与锐角的差一定是钝角。
故答案为: √
【点睛】熟练掌握平角、锐角和钝角的定义是解决本题的关键。一个平角可以分成两个直角
或者一个锐角和一个钝角。
9 .C
【分析】读图可知, ∠1 和∠2 组成一个平角, ∠2 和∠3 组成一个平角, 则∠1 = ∠3,且∠2+∠3
= 180° 。∠ 1 和∠4 组成一个平角,则∠2 = ∠4。
【详解】根据分析可知, ∠ 1 = ∠3 ,∠2 = ∠4 ,∠2+∠3 =180°。
故答案为: C。
【点睛】解决本题的关键是明确平角为 180°。
10 .B
【分析】由正方形的特征可知,正方形有 4 条边、4 个角,4 个角都是直角;根据图形可知,
∠ 1 是正方形一个直角度数的一半,所以∠1 =90°÷2 =45°,据此解题即可。
【详解】根据分析可知, ∠ 1 =90°÷2 =45°。
故答案为: B
【点睛】熟记正方形的身高角是直角,是解答此题的关键。
11 .C
12 .C
【分析】平角是 180 度, 其中钝角是大于 90°, 小于 180°的角, 用“180°-钝角 ”所得的角的
度数小于 90 度,根据锐角的含义:大于 0 度,小于 90 度的角叫做锐角;进而得出结论。
【详解】由分析可知:
把一个平角分成两个角,其中一个是钝角,那么另一个角一定是锐角。
故答案为: C
【点睛】此题考查了锐角、平角和钝角的含义,应注意知识的灵活运用。
13 .图中②是直角, ③④比直角大, ①比直角小
14 .见详解
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,
角的另一边所对的量角器上的刻度, 就是这个角的度数, 依此测量即可。小于 90°的角是锐
角,等于 90°的角是直角,大于 90°小于 180°的角是钝角,依此填空即可。
【详解】
【点睛】此题考查的是角的度量,以及角的分类,应熟练掌握。
15 .
五边形 5 个角
【分析】具有公共端点的两条射线组成的图形叫做角。这个公共端点叫做角的顶点, 这两条
射线叫做角的两条边。直角是指等于 90°的角。据此数出即可。
【详解】五边形,五个角。
16 . ∠ 1=50°
∠2=60°
∠3=70°
【详解】 110°+130°=240°
∠2=240°-180°=60°
∠ 1=110°-∠2=110°-60°=50°
∠3=130°-∠2=130°-60°=70°
17 .100°
【详解】(360°-60°)÷3=100°
18 .见详解
【分析】钟面上 12 个数字, 以表芯为旋转点, 表针转一圈是 360°, 被 12 个数字平均分成 12 份,每一份也就是两数之间夹角是 30° 。10 时整,时针指向 10,分针指向 12,时针和分针 之间的夹角是: 2×30° =60°,是锐角。 1 时半,时针指在 1 与 2 之间,分针指向 6,时针和
分针之间的夹角是: 4×30°+30°÷2 =135°;据此解答即可。
【详解】2×30° =60°
4×30°+30°÷2
= 120°+15°
= 135°
所以, 10 时整,时针和分针成锐角, 1 时半,时针和分针成钝角。
画图如下:
【点睛】钟面上每相邻两个数字之间的夹角是 30°。小于 90°的角是锐角;大于 90°且小于 180°
的角为钝角。
19 . ∠ 1=110° ∠2==70° ∠3=110°
【详解】∠1=180°-∠4=180°-70°=110°
∠2=180°-∠ 1=180°-110°=70°
∠3=180°-∠4=180°-70°=110°
一、填空题
1 .下图中,已知∠1+∠5 =138°,那么: ∠2 =( )° , ∠3 =( )°。
2 .下图中有( )个直角,有( )个钝角,有( )锐角。
3 .观察下面各个角,把合适的角填入合适的括号中。
锐角有:( ) 钝角有:( )
直角有:( ) 平角有:( )
4.下图中锐角有( )个,直角有( )个,钝角有( )个,平角有( )个。
二、判断题
5 .三个角组成一个平角,这三个角可能都是锐角。 ( )
6 .一个平角减去一个锐角,得到一个钝角.( )
7 .钟面上是 6 时整时,时针和分针所夹的角是平角。 ( )
8 .平角与锐角的差一定是钝角。 ( )
三、选择题
9 .下图中各角关系正确的是( )。
A . ∠ 1 = ∠2 B . ∠3 = ∠4 C . ∠2+∠3 =180°
10 .如图:正方形∠1=( ) °。
A .60° B .45° C .30°
11 . ∠ 1+∠2=平角,已知∠2 是锐角,则∠1 一定是( )
A .锐角 B .直角 C .钝角
12 .把一个平角分成两个角,其中一个是钝角,那么另一角肯定是( )。
A .直角 B .钝角 C .锐角
四、解答题
13.钟面上时针和分针组成的角, 哪一个是直角?哪一个角比直角大?哪一个角比直角
小?
14 .量出下面各角分别是多少度,并在图上标出来。再写出它们各是什么角。
( ) ( ) ( ) ( )
15 .下面的图形是几边形?有几个角?是直角的要画上标记。
16 .下图中, ∠ 1+∠2 =110° , ∠2+∠3=130°,你知道∠1 、∠2 、∠3 各是多少度吗?
17 .一个角的 3 倍比周角少 60°,这个角是多少度?
18.根据给定的时刻, 在钟面上画出时针和分针, 并判断(写出)时针和分针成什么角?
10 时 1 时半
( )角 ( )角
19 .如下图所示, 已知∠4=70°,求∠1,∠2 和∠3 的度数.
1 . 42 138
【分析】∠1+∠5+∠2 等于平角是 180°,让 180°减去 138°就是∠2 的度数; ∠2+∠3 等于平
角是 180°,让 180°减去∠2 的度数即可求解∠3,据此解答。
【详解】因为∠1+∠5+∠2 =180°,所以∠2 =180°-138° =42°
∠2+∠3 =180° , ∠3 =180°-42° = 138°
【点睛】本题考查角的分类和计算,掌握平角是 180 度是解题的关键。
2 . 1 1 4
3 . ∠2 ,∠4 ,∠8 ,∠ 12 ∠3 ,∠7 ,∠9 ,∠ 11 ∠ 1 ,∠5 ,∠ 10 ∠6
4 . 10 4 2 4
【分析】根据长方形的特征,每个角都是直角,根据角的分类, 0°<锐角<90°,直角=
90° , 90°<钝角<180°,平角=180°;据此解答。
【详解】锐角有 10 个:∠DAC 、∠CAB 、∠ABD 、∠DBC 、∠BCA 、∠ACD 、∠CDB 、∠BDA、
∠AOD 、∠BOC;直角有 4 个: ∠ABC 、∠BCD 、∠ADC 、∠BAD;钝角有 2 个: ∠AOB、
∠COD;平角有 4 个: ∠AOC 、∠BOD 、∠COA 、∠DOB。
【点睛】本题考查角的分类,关键注意在数角过程中不要漏数。
5 . √
【分析】小于 90°的角是锐角, 等于 90°的角是直角, 大于 90°小于 180°的角是钝角, 等于 180°
的角是平角,依此判断即可。
【详解】90°+30°+60° = 180°,此时 1 个直角、 2 个锐角组成一个平角。
80°+60°+40° = 180°,此时 3 个锐角组成一个平角。
100°+50°+30° = 180°,此时 1 个钝角、 2 个锐角组成一个平角。
故答案为: √
【点睛】熟练掌握角的分类标准,是解答此题的关键。
6 . √
7 . √
8 . √
【分析】平角是 180°的角, 锐角是小于 90°的角, 平角与锐角的差是大于 90°小于 180°。而
大于 90°小于 180°的角是钝角。据此判断。
【详解】根据分析可知,平角与锐角的差一定是钝角。
故答案为: √
【点睛】熟练掌握平角、锐角和钝角的定义是解决本题的关键。一个平角可以分成两个直角
或者一个锐角和一个钝角。
9 .C
【分析】读图可知, ∠1 和∠2 组成一个平角, ∠2 和∠3 组成一个平角, 则∠1 = ∠3,且∠2+∠3
= 180° 。∠ 1 和∠4 组成一个平角,则∠2 = ∠4。
【详解】根据分析可知, ∠ 1 = ∠3 ,∠2 = ∠4 ,∠2+∠3 =180°。
故答案为: C。
【点睛】解决本题的关键是明确平角为 180°。
10 .B
【分析】由正方形的特征可知,正方形有 4 条边、4 个角,4 个角都是直角;根据图形可知,
∠ 1 是正方形一个直角度数的一半,所以∠1 =90°÷2 =45°,据此解题即可。
【详解】根据分析可知, ∠ 1 =90°÷2 =45°。
故答案为: B
【点睛】熟记正方形的身高角是直角,是解答此题的关键。
11 .C
12 .C
【分析】平角是 180 度, 其中钝角是大于 90°, 小于 180°的角, 用“180°-钝角 ”所得的角的
度数小于 90 度,根据锐角的含义:大于 0 度,小于 90 度的角叫做锐角;进而得出结论。
【详解】由分析可知:
把一个平角分成两个角,其中一个是钝角,那么另一个角一定是锐角。
故答案为: C
【点睛】此题考查了锐角、平角和钝角的含义,应注意知识的灵活运用。
13 .图中②是直角, ③④比直角大, ①比直角小
14 .见详解
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,
角的另一边所对的量角器上的刻度, 就是这个角的度数, 依此测量即可。小于 90°的角是锐
角,等于 90°的角是直角,大于 90°小于 180°的角是钝角,依此填空即可。
【详解】
【点睛】此题考查的是角的度量,以及角的分类,应熟练掌握。
15 .
五边形 5 个角
【分析】具有公共端点的两条射线组成的图形叫做角。这个公共端点叫做角的顶点, 这两条
射线叫做角的两条边。直角是指等于 90°的角。据此数出即可。
【详解】五边形,五个角。
16 . ∠ 1=50°
∠2=60°
∠3=70°
【详解】 110°+130°=240°
∠2=240°-180°=60°
∠ 1=110°-∠2=110°-60°=50°
∠3=130°-∠2=130°-60°=70°
17 .100°
【详解】(360°-60°)÷3=100°
18 .见详解
【分析】钟面上 12 个数字, 以表芯为旋转点, 表针转一圈是 360°, 被 12 个数字平均分成 12 份,每一份也就是两数之间夹角是 30° 。10 时整,时针指向 10,分针指向 12,时针和分针 之间的夹角是: 2×30° =60°,是锐角。 1 时半,时针指在 1 与 2 之间,分针指向 6,时针和
分针之间的夹角是: 4×30°+30°÷2 =135°;据此解答即可。
【详解】2×30° =60°
4×30°+30°÷2
= 120°+15°
= 135°
所以, 10 时整,时针和分针成锐角, 1 时半,时针和分针成钝角。
画图如下:
【点睛】钟面上每相邻两个数字之间的夹角是 30°。小于 90°的角是锐角;大于 90°且小于 180°
的角为钝角。
19 . ∠ 1=110° ∠2==70° ∠3=110°
【详解】∠1=180°-∠4=180°-70°=110°
∠2=180°-∠ 1=180°-110°=70°
∠3=180°-∠4=180°-70°=110°
