河北省石家庄市第二实验中学高中数学课件 必修一:2.2.2对数函数及其性质——反函数
文档属性
| 名称 | 河北省石家庄市第二实验中学高中数学课件 必修一:2.2.2对数函数及其性质——反函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-02 00:00:00 | ||
图片预览


文档简介
课件32张PPT。2.2.2 对 数 函 数
及其性质(二) 函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,函数的定义域是( 0 , +∞)
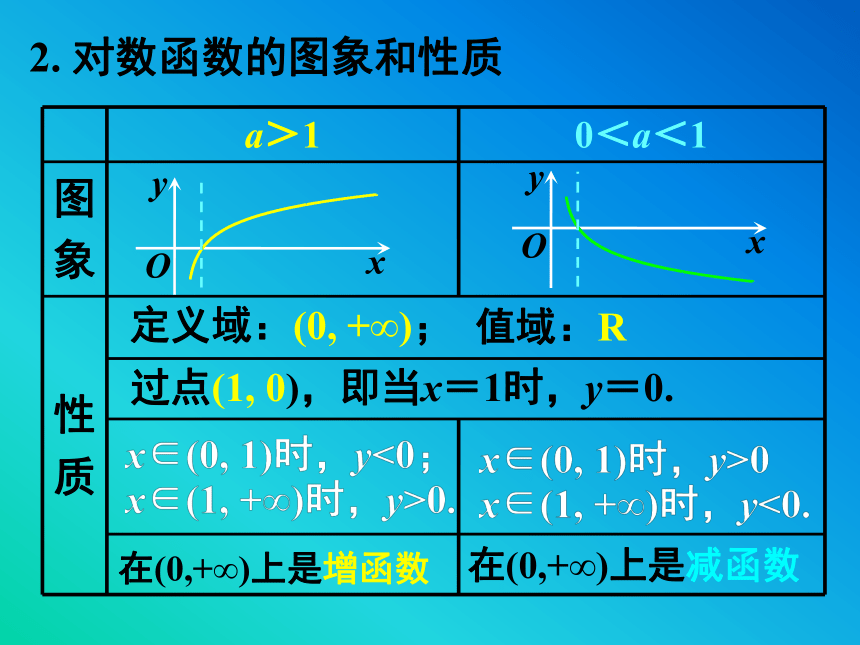
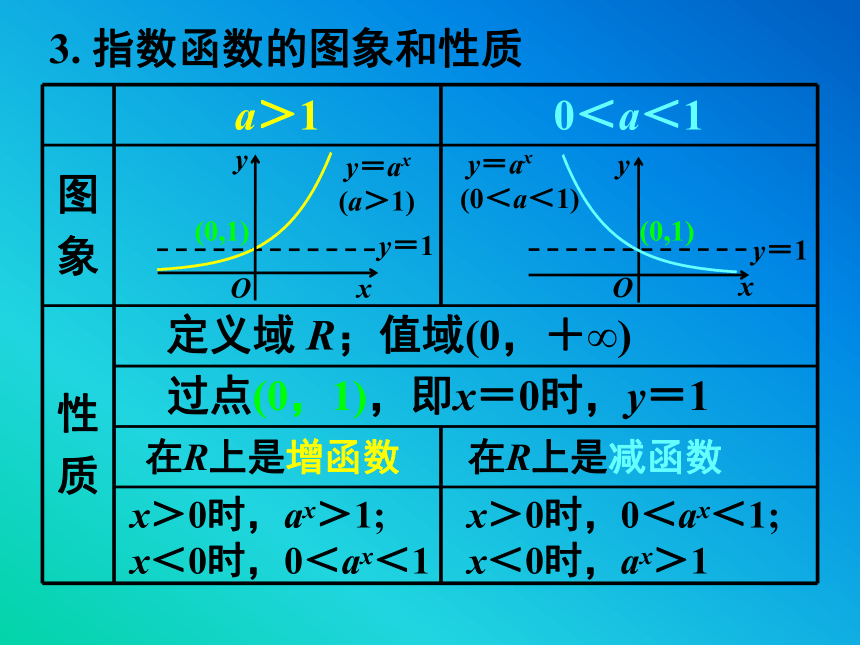
1.对数函数的定义:定义域:(0, +∞); 值域:R 过点(1, 0),即当x=1时,y=0. 在(0,+∞)上是减函数 在(0,+∞)上是增函数 2. 对数函数的图象和性质 y=1 y=1(0,1)(0,1)3. 指数函数的图象和性质过点(0,1),即x=0时,y=1在R上是增函数在R上是减函数x>0时,ax>1;
x<0时,0<ax<1x>0时,0<ax<1;
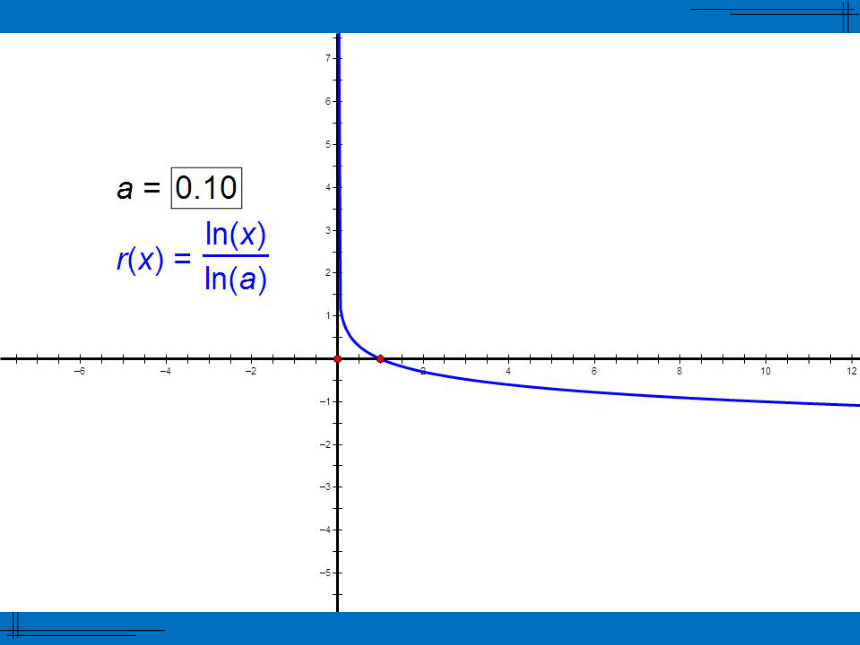
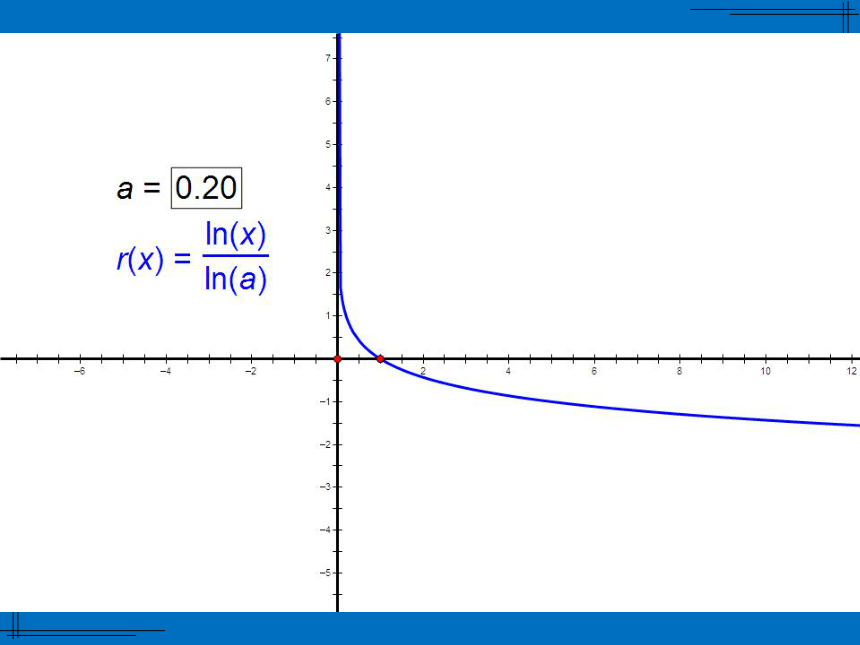
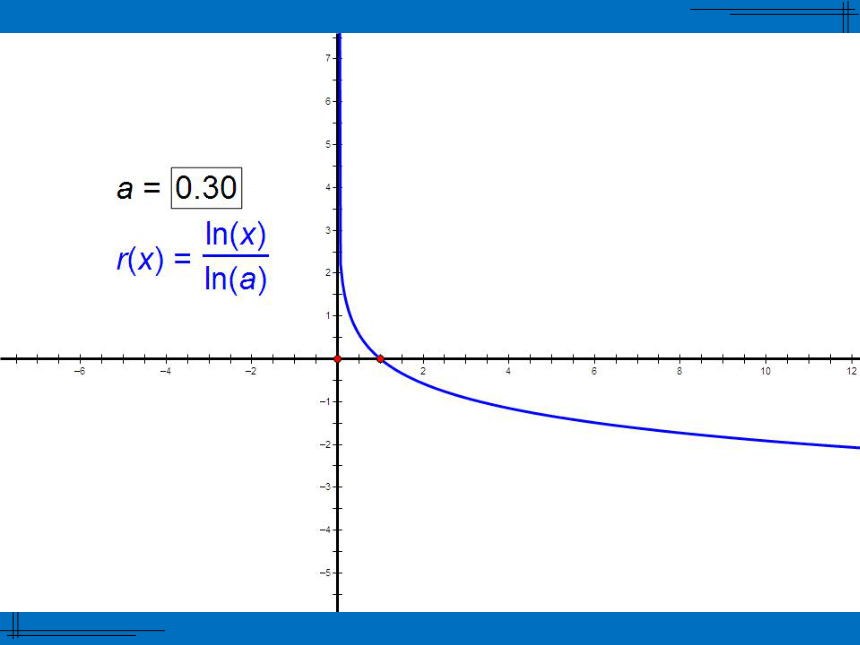
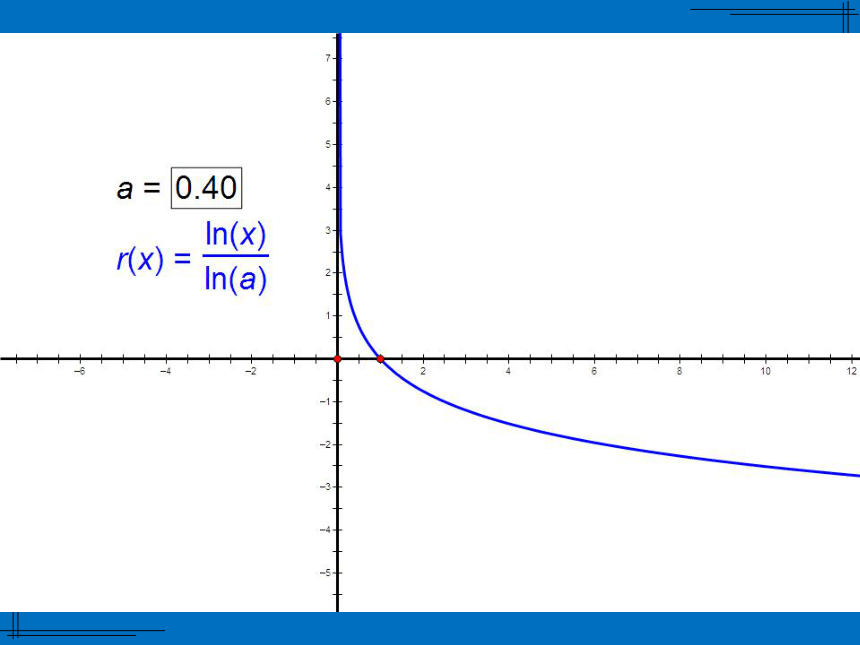
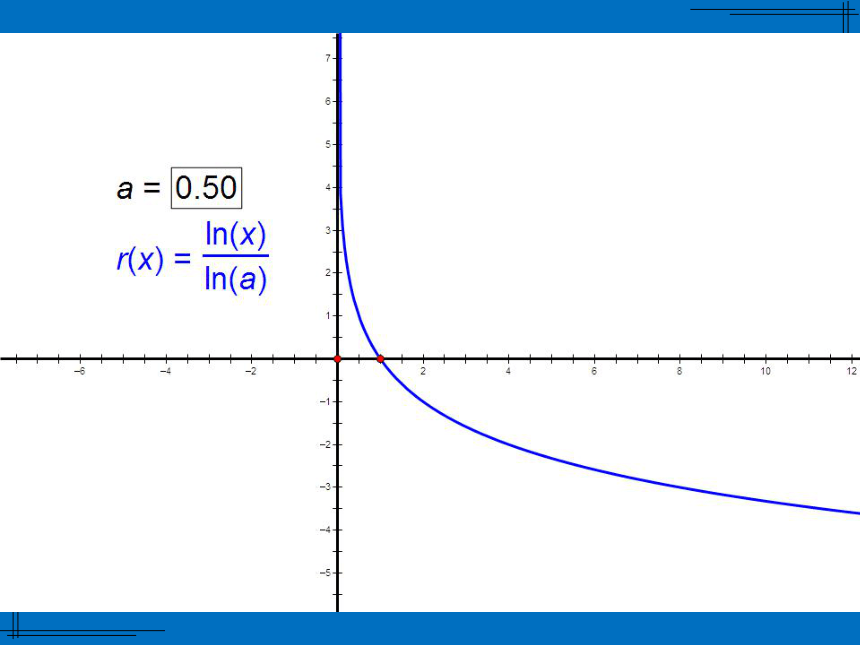
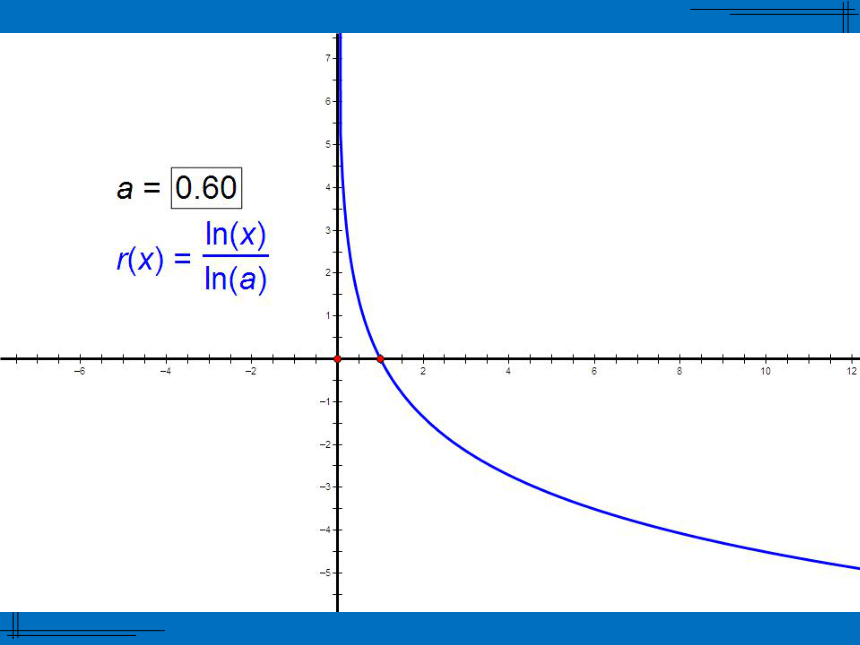
x<0时,ax>1定义域 R;值域(0,+∞) 当a>1时,a值越大,函数图像越靠近x轴;
当0 ⑴log 27 , log 3 7 ; x=7x=4 在指数函数 中,x为自变量,y为因变量.如果把y当成自变量,x当成因变量,那么x是y的函数吗?如果是,那么对应关系是什么?如果不是,请说明理由.结论1:同底的指数函数与对数函数互为反函数.(1)函数 与函数 的图象有什么关系?(2)函数 与函数
的图象有什么关系?结论2:互为反函数的两个函数图象关于直线y=x对称.二、反函数的有关概念与性质: y=log2xo(1,0)(0,1)y=x y=logax(01时,a值越大,函数图像越靠近x轴;当0 B: 2
精讲精练:
P48~49:1~5;9、11、12.
及其性质(二) 函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,函数的定义域是( 0 , +∞)
1.对数函数的定义:定义域:(0, +∞); 值域:R 过点(1, 0),即当x=1时,y=0. 在(0,+∞)上是减函数 在(0,+∞)上是增函数 2. 对数函数的图象和性质 y=1 y=1(0,1)(0,1)3. 指数函数的图象和性质过点(0,1),即x=0时,y=1在R上是增函数在R上是减函数x>0时,ax>1;
x<0时,0<ax<1x>0时,0<ax<1;
x<0时,ax>1定义域 R;值域(0,+∞) 当a>1时,a值越大,函数图像越靠近x轴;
当0
的图象有什么关系?结论2:互为反函数的两个函数图象关于直线y=x对称.二、反函数的有关概念与性质: y=log2xo(1,0)(0,1)y=x y=logax(0
精讲精练:
P48~49:1~5;9、11、12.
