河北省石家庄市第二实验中学高中数学课件 必修五:2.2等差数列
文档属性
| 名称 | 河北省石家庄市第二实验中学高中数学课件 必修五:2.2等差数列 |  | |
| 格式 | zip | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-02 07:28:44 | ||
图片预览










文档简介
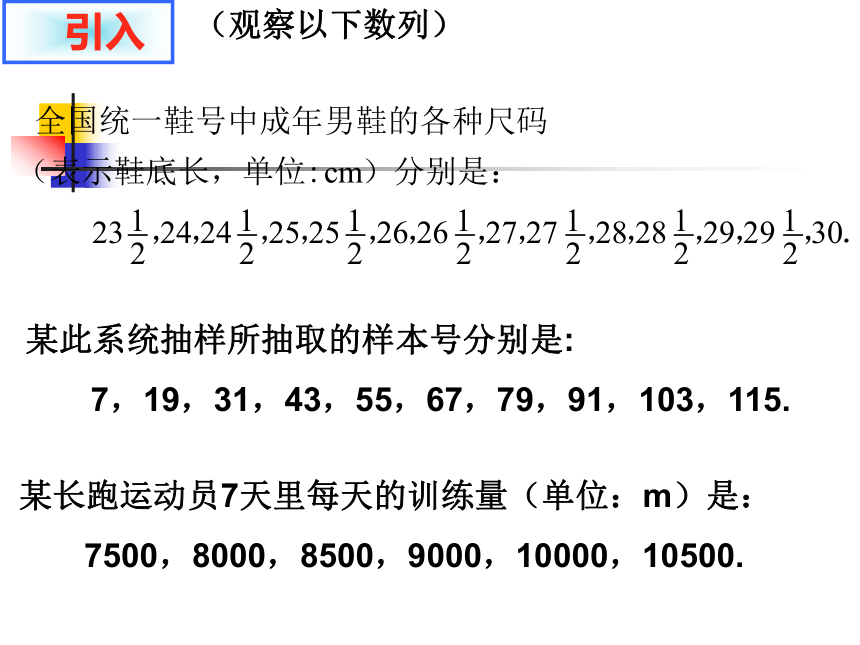
课件30张PPT。2.2 等差数列第二章 数列 第一课时 一、数列的定义,通项公式:按一定次序排成的一列数叫做数列。一般写成a1,a2,a3 ,… an,… 如果数列{an}的第n项an与n的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式。二、数列的简单表示:三、给出数列的方法:www.jkzyw.com 复习某此系统抽样所抽取的样本号分别是:
7,19,31,43,55,67,79,91,103,115.某长跑运动员7天里每天的训练量(单位:m)是:
7500,8000,8500,9000,10000,10500.(观察以下数列) 引入这三个数列有何共同特征从第2项起,每一项与其前一项之差等于同一个常数。请尝试着给具有上述特征的特殊数列
用数学的语言下定义 交流1、等差数列的定义
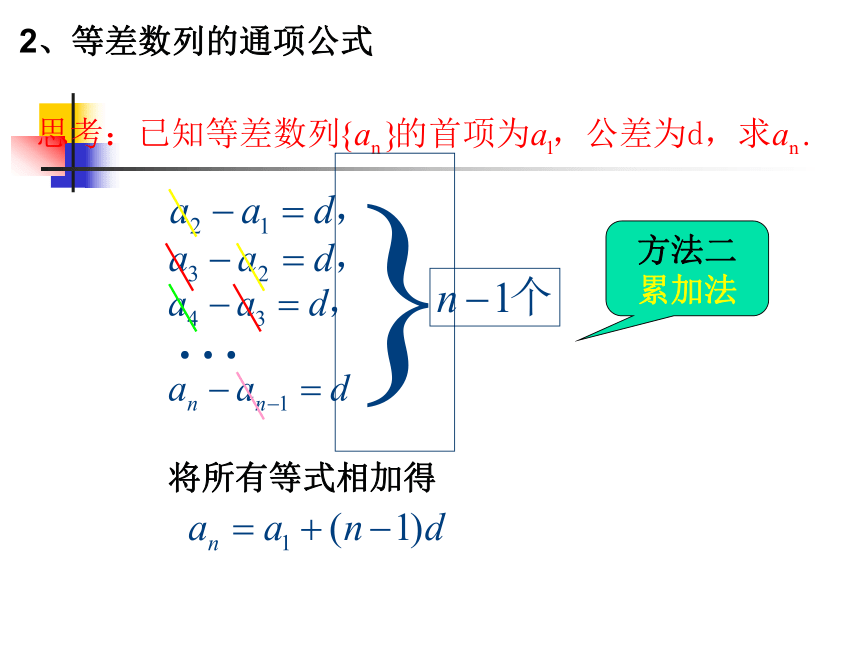
如果一个数列从第2项起,每一项与其前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。(1)指出定义中的关键词:从第2项起等于同一个常数⑵由定义得等差数列的递推公式: 说明:此公式是判断、证明一个数列是否为等差数列的主要依据.每一项与其前一项的差 探究 练习:判断下列数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d, 如果不是,说明理由。www.jkzyw.com2、等差数列的通项公式根据等差数列的定义得到方法一:不完全归纳法2、等差数列的通项公式将所有等式相加得方法二
累加法例1 ⑴求等差数列8,5,2,…的第20项.
⑵- 401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?解:⑴由a1=8,d=5-8=-3,n=20,得
a20=8+(20-1) ×(-3)=-49.⑵由a1=-5,d =-9-(-5)=-4,得到这个数列的通项公式为an=-5-4(n-1).
由题意得-401=-5-4(n-1),解这个关于n的方程,得n=100,即-401是这个数列的第100项.例2 在等差数列{an}中,已知
a5=10,a12=31,求首项a1与公差d .这是一个以a1和d 为未知数的二元一次方程组,解之得:小结:已知数列中任意两项,可求出首项和公差,主要是联立二元一次方程组。这种题型有简便方法吗?请同学们思考并做以下练习。1、已知等差数列的首项与公差,可求得其任何一项;2、在等差数列的通项公式中,a1,d,n,an四个量中知三求一.结论 跟踪训练3.等差中项 如果 a, A, b 成等差数列,那么 A 叫做 a 与 b 的等差中项 .由等差中项的定义可知, a, A, b 满足关系:意义:
任意两个数都有等差中项,并且这个等差中项是唯一的.当 a=b 时,A = a = b .例3 (1)在等差数列{an}中,是否有
(2)在数列{an}中,如果对于任意的正整数n(n≥2),都有
那么数列{an}一定是等差数列吗?4、等差数列通项公式的推广解析:由等差数列的通项公式得思考:已知等差数列{an}中,a3=9,a9=3,求a12,a3n.解法一: 依题意得:
a1+2d=9
a1+8d=3
解之得 a1 =11
d =-1∴这个数列的通项公式是:an=11- (n-1)=12-n
故 a12= 0, a 3n = 12 – 3 n.解法二:课本P40(A) 1、3、
(B) 2 作业2.2 等差数列第二章 数列 第二课时 2、等差数列的通项公式1、等差数列的定义3、等差数列的中项 复习通项公式的证明及推广100与180例4例5 已知三个数成等差数列,它们的和是12,积是48,求这三个数. 解:设三个数为a-d,a,a+d,则解之得故所求三数依次为2,4,6或6,4,2例6 如图,三个正方形的边AB,BC,CD的长组成等差数列,且AD=21cm,这三个正方形的面积之和是179cm2.
(1)求AB,BC,CD的长;
(2)以 AB,BC,CD的长为等差数列的前三项,以第9项为边长的正方形的面积是多少?3,7,11a9=35S9=12255、等差数列的通项及图象特征解析: 思考结论:首项是1,公差是2的无穷等差数列的通项公式为an =2n-1相应的图象是直线y=2x-1上均匀排开的无穷多个孤立的点,如右图例如:5、等差数列的性质已知数列 为等差数列,那么有性质1:若 成等差数列,则
成等差数列.证明:根据等差数列的定义,即 成等差数列.如 成等差数列, 成等差数列.推广:在等差数列有规律地取出若干项,所得新数列仍然为等差数列。(如奇数项,项数是7的倍数的项)性质2:设 若 则性质3:设 c, b 为常数,若数列 为等差数列,则数
列 及 为等差数列.性质4:设 p, q 为常数,若数列 、 均为等差数列,
则数列 为等差数列.例8(1)已知等差数列{an}中, a3 +a15=30,求a9, a7+a11解:(1)∵a9是a3和a15的等差中项∴(2)已知等差数列{an}中, a3 +a4+a5 +a6 +a7=150,求a2+a8的值∵7+11=3+15(2)∵3+7=4+6=5+5∴ a3 +a4+a5 +a6 +a7=5 a5=150即a5=30故a2+a8 =2 a5=60∴ a7+a11 =a3 +a15=30∴ a3+a7 =a4 +a6=2 a5(1)等差数列{an}中,a3 +a9+a15+a21=8,则a12 = (2)已知等差数列{an}中, a3 和a15是方程x2-6x-1=0的两个根,则a7 +a8 +a9+a10+a11= 2 (3)已知等差数列{an}中, a3 +a5= -14, 2a2+a6 = -15,则a8=-19 跟踪训练
7,19,31,43,55,67,79,91,103,115.某长跑运动员7天里每天的训练量(单位:m)是:
7500,8000,8500,9000,10000,10500.(观察以下数列) 引入这三个数列有何共同特征从第2项起,每一项与其前一项之差等于同一个常数。请尝试着给具有上述特征的特殊数列
用数学的语言下定义 交流1、等差数列的定义
如果一个数列从第2项起,每一项与其前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示。(1)指出定义中的关键词:从第2项起等于同一个常数⑵由定义得等差数列的递推公式: 说明:此公式是判断、证明一个数列是否为等差数列的主要依据.每一项与其前一项的差 探究 练习:判断下列数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d, 如果不是,说明理由。www.jkzyw.com2、等差数列的通项公式根据等差数列的定义得到方法一:不完全归纳法2、等差数列的通项公式将所有等式相加得方法二
累加法例1 ⑴求等差数列8,5,2,…的第20项.
⑵- 401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?解:⑴由a1=8,d=5-8=-3,n=20,得
a20=8+(20-1) ×(-3)=-49.⑵由a1=-5,d =-9-(-5)=-4,得到这个数列的通项公式为an=-5-4(n-1).
由题意得-401=-5-4(n-1),解这个关于n的方程,得n=100,即-401是这个数列的第100项.例2 在等差数列{an}中,已知
a5=10,a12=31,求首项a1与公差d .这是一个以a1和d 为未知数的二元一次方程组,解之得:小结:已知数列中任意两项,可求出首项和公差,主要是联立二元一次方程组。这种题型有简便方法吗?请同学们思考并做以下练习。1、已知等差数列的首项与公差,可求得其任何一项;2、在等差数列的通项公式中,a1,d,n,an四个量中知三求一.结论 跟踪训练3.等差中项 如果 a, A, b 成等差数列,那么 A 叫做 a 与 b 的等差中项 .由等差中项的定义可知, a, A, b 满足关系:意义:
任意两个数都有等差中项,并且这个等差中项是唯一的.当 a=b 时,A = a = b .例3 (1)在等差数列{an}中,是否有
(2)在数列{an}中,如果对于任意的正整数n(n≥2),都有
那么数列{an}一定是等差数列吗?4、等差数列通项公式的推广解析:由等差数列的通项公式得思考:已知等差数列{an}中,a3=9,a9=3,求a12,a3n.解法一: 依题意得:
a1+2d=9
a1+8d=3
解之得 a1 =11
d =-1∴这个数列的通项公式是:an=11- (n-1)=12-n
故 a12= 0, a 3n = 12 – 3 n.解法二:课本P40(A) 1、3、
(B) 2 作业2.2 等差数列第二章 数列 第二课时 2、等差数列的通项公式1、等差数列的定义3、等差数列的中项 复习通项公式的证明及推广100与180例4例5 已知三个数成等差数列,它们的和是12,积是48,求这三个数. 解:设三个数为a-d,a,a+d,则解之得故所求三数依次为2,4,6或6,4,2例6 如图,三个正方形的边AB,BC,CD的长组成等差数列,且AD=21cm,这三个正方形的面积之和是179cm2.
(1)求AB,BC,CD的长;
(2)以 AB,BC,CD的长为等差数列的前三项,以第9项为边长的正方形的面积是多少?3,7,11a9=35S9=12255、等差数列的通项及图象特征解析: 思考结论:首项是1,公差是2的无穷等差数列的通项公式为an =2n-1相应的图象是直线y=2x-1上均匀排开的无穷多个孤立的点,如右图例如:5、等差数列的性质已知数列 为等差数列,那么有性质1:若 成等差数列,则
成等差数列.证明:根据等差数列的定义,即 成等差数列.如 成等差数列, 成等差数列.推广:在等差数列有规律地取出若干项,所得新数列仍然为等差数列。(如奇数项,项数是7的倍数的项)性质2:设 若 则性质3:设 c, b 为常数,若数列 为等差数列,则数
列 及 为等差数列.性质4:设 p, q 为常数,若数列 、 均为等差数列,
则数列 为等差数列.例8(1)已知等差数列{an}中, a3 +a15=30,求a9, a7+a11解:(1)∵a9是a3和a15的等差中项∴(2)已知等差数列{an}中, a3 +a4+a5 +a6 +a7=150,求a2+a8的值∵7+11=3+15(2)∵3+7=4+6=5+5∴ a3 +a4+a5 +a6 +a7=5 a5=150即a5=30故a2+a8 =2 a5=60∴ a7+a11 =a3 +a15=30∴ a3+a7 =a4 +a6=2 a5(1)等差数列{an}中,a3 +a9+a15+a21=8,则a12 = (2)已知等差数列{an}中, a3 和a15是方程x2-6x-1=0的两个根,则a7 +a8 +a9+a10+a11= 2 (3)已知等差数列{an}中, a3 +a5= -14, 2a2+a6 = -15,则a8=-19 跟踪训练
