江苏省南京市联合体学校2023~2024学年上学期八年级上学期期中数学试题(含答案)
文档属性
| 名称 | 江苏省南京市联合体学校2023~2024学年上学期八年级上学期期中数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 09:06:51 | ||
图片预览


文档简介
2023~2024学年度第一学期期中学情分析样题
八年级数学
注意事项:
1.本试卷共6页.全卷满分100分.考试时间为100分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.下面是各届亚运会的会标,其中是轴对称图形的是
A. B. C. D.
2.下列各组数中,是勾股数的是
A.1,2,3 B.2,3,4 C.4,5,6 D.6,8,10
3.如图,用纸板挡住了三角形的一部分,小明根据所学知识重新画出了一个与原来完全一样的三角形,他的依据是
A.AAS B.ASA C.SAS D.SSS
(
(第
3
题)
(第
4
题)
D
B
C
A
E
)
(
(第
5
题)
1
3m
5m
)
4.如图,△ABC≌△ADE,∠B=30°,∠E=100°,∠CAD=20°,则∠BAD的度数为
A.20° B.25° C.30° D.50°
5.下列条件能判断△ABC为等腰三角形的是
A.∠A=40°,∠B=50° C.∠A=40°,∠B=70° B.∠A=40°,∠B=60° D.∠A=40°,∠B=80°
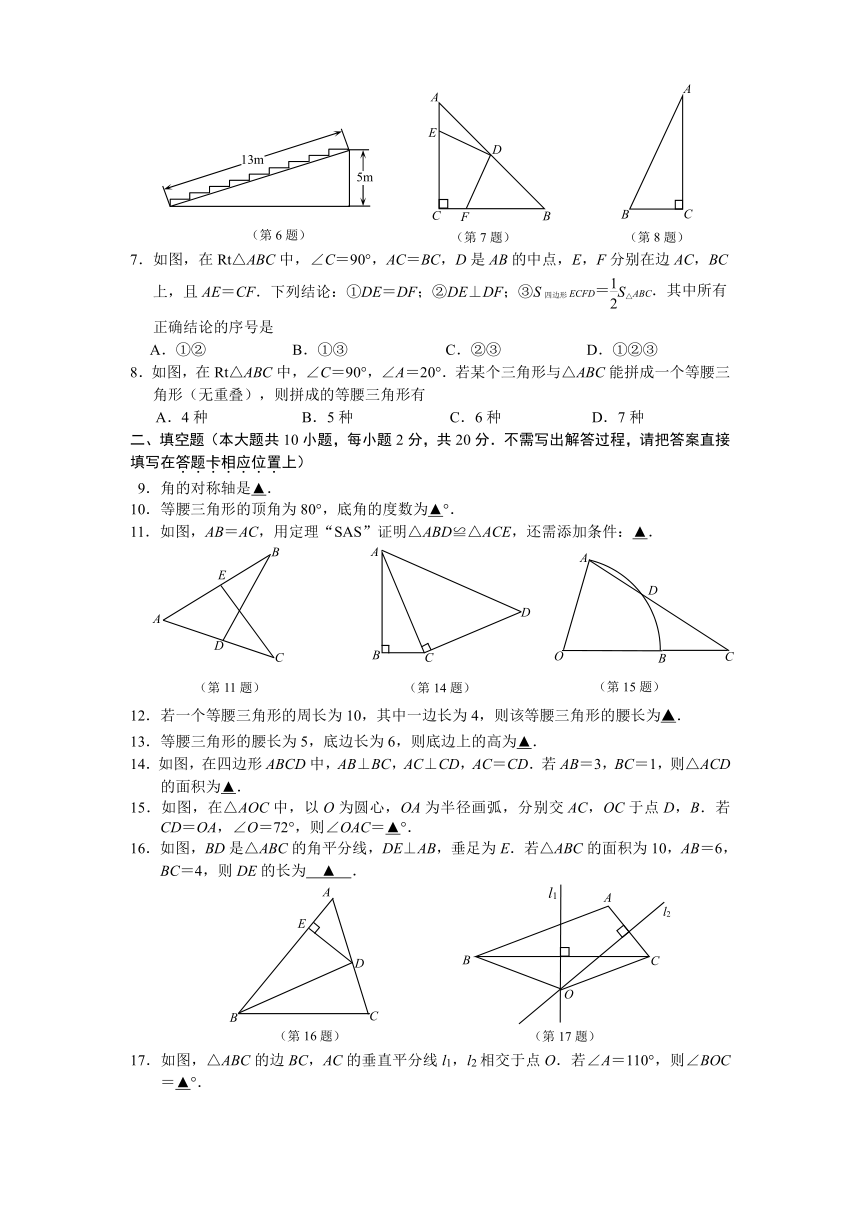
6.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要
A.13m B.17m C.18m D.25m
(
(第
6
题)
13m
5m
A
C
B
(第
8
题)
A
C
B
D
E
F
(第
7
题)
)
7.如图,在Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,E,F分别在边AC,BC上,且AE=CF.下列结论:①DE=DF;②DE⊥DF;③S四边形ECFD=S△ABC.其中所有正确结论的序号是
A.①② B.①③ C.②③ D.①②③
8.如图,在Rt△ABC中,∠C=90°,∠A=20°.若某个三角形与△ABC能拼成一个等腰三角形(无重叠),则拼成的等腰三角形有
A.4种 B.5种 C.6种 D.7种
二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9.角的对称轴是▲.
10.等腰三角形的顶角为80°,底角的度数为▲°.
(
A
B
C
D
(
第
14
题
)
A
B
C
D
E
(
第
11
题
)
A
C
B
D
O
(
第
15
题
)
)11.如图,AB=AC,用定理“SAS”证明△ABD≌△ACE,还需添加条件:▲.
12.若一个等腰三角形的周长为10,其中一边长为4,则该等腰三角形的腰长为▲.
13.等腰三角形的腰长为5,底边长为6,则底边上的高为▲.
14.如图,在四边形ABCD中,AB⊥BC,AC⊥CD,AC=CD.若AB=3,BC=1,则△ACD 的面积为▲.
15.如图,在△AOC中,以O为圆心,OA为半径画弧,分别交AC,OC于点D,B.若CD=OA,∠O=72°,则∠OAC=▲°.
(
A
B
C
D
E
(
第
16
题
)
O
l
1
l
2
B
C
A
(
第
17
题
)
)16.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.若△ABC的面积为10,AB=6,BC=4,则DE的长为 ▲ .
17.如图,△ABC的边BC,AC的垂直平分线l1,l2相交于点O.若∠A=110°,则∠BOC=▲°.
18.在△ABC中,∠A=30°,AB=2.若对于BC的每一个值,对应的△ABC的形状、大小都唯一确定,则BC长的取值范围是▲.
三、解答题(本大题共8小题,共64分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(7分)如图,在边长为1个单位长度的小正方形组成的网格中,点A,B在小正方形的顶点上.
(1)在图中画出与线段AB关于直线l成轴对称的线段A′B′;
(2)在直线l上确定一点P,使PA+PB最短.
(
A
B
l
(第
19
题)
)
(
(第
20
题)
A
C
1
2
B
E
)20.(7分)如图,AC=AE,∠1=∠2,AB=AD.求证BC=DE.
(
D
)
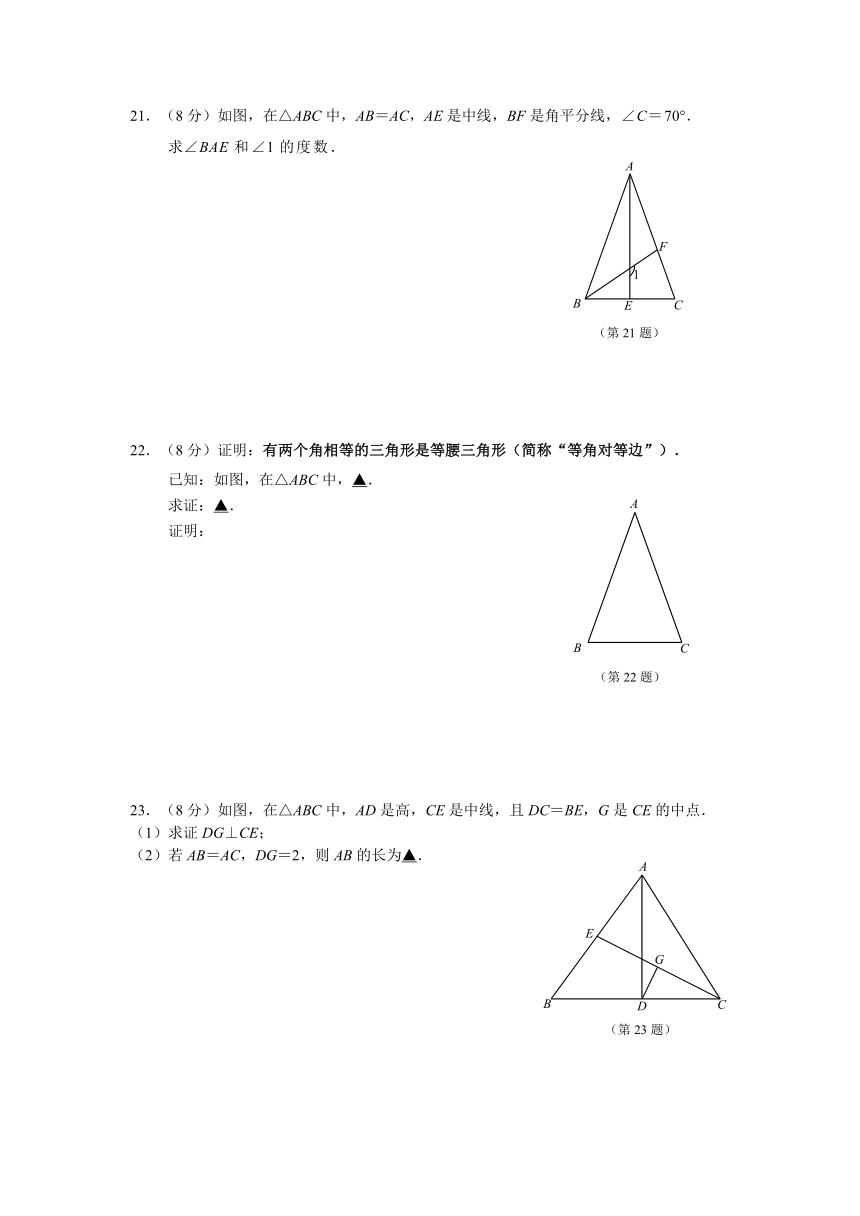
21.(8分)如图,在△ABC中,AB=AC,AE是中线,BF是角平分线,∠C=70°.
(
A
B
C
(第
2
1
题)
E
F
1
)求∠BAE和∠1的度数.
22.(8分)证明:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
(
A
B
C
(第
22
题)
)已知:如图,在△ABC中,▲.
求证:▲.
证明:
23.(8分)如图,在△ABC中,AD是高,CE是中线,且DC=BE,G是CE的中点.
(1)求证DG⊥CE;
(
A
B
C
D
E
G
(第
2
3
题)
)(2)若AB=AC,DG=2,则AB的长为▲.
24.(8分)如图,AB⊥BC,DC⊥BC,垂足分别为B,C,DE交BC于点E,AB=EC,AC=DE.
(1)求证AC⊥DE;
(
A
B
C
D
E
(第
24
题)
)(2)连接AD,若AB=a,BC=b,AC=c,通过用不同方法计算四边形ABCD的面积,验证勾股定理.
25.(8分)如图,已知线段a和∠MAN.在边AM上作点B,在边AN上作点C,分别满足下列条件:
(1)在图①中,AB=a,AC=BC;
(2)在图②中,BC=a,AB=AC.
(要求:用直尺和圆规作图,保留作图痕迹,写出必要的文字说明).
(
a
A
N
M
A
N
M
①
②
)
26.(10分)
【概念认识】
定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.当这个点是直角的顶点时,这个点又称为强勾股点.
(
C
A
B
①
)如图①,在Rt△ABC中,∠C=90°,A是B,C两点的勾股点,B是A,C两点的勾股点,C是A,B两点的勾股点,也是强勾股点.
(
②
A
B
C
D
)
【概念运用】
(1)如图②,方格纸中的每个小正方形的边长均为1,A,B两点均在格点上,线段CD上的8个格点中,是A,B两点的勾股点的有▲个.
(
C
A
B
D
③
)(2)如图③,在△ABC中,CD⊥AB,垂足为D,若AD=1,BD=4,CD=2.
(
C
A
B
D
)求证:C是A,B两点的强勾股点.
【拓展提升】
(
C
A
B
D
④
)(3)如图④,在Rt△ABC中,∠C=90°,AC=6,BC=4,D是AC的中点,P是射线BD上一个动点,当P是Rt△ABC任意两个顶点的强勾股点时,直接写出BP的长.
2023-2024学年度第一学期期中学情分析样题
八年级数学参考答案
说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.
一、选择题 (本大题共8小题,每小题2分,共16分)
题号 1 2 3 4 5 6 7 8
答案 C D B C C B D D
二、填空题 (本大题共10小题,每小题2分,共20分)
9.角平分线所在的直线 10.50° 11.AE=AD 12.3或4 13.4
(
C
A
B
l
(第
19
题)
A'
B
'
P
)14.5 15.72° 16.2 17.140° 18.BC=1或BC≥2
三、解答题(本大题共8小题,共64分)
19.(7分)
(1)画对A′B′;……………………4分
(2)画对点P.……………………7分
20.(7分)
证明:∵∠1=∠2,
(
D
(第
20
题)
A
C
1
2
E
)∴∠1+∠EAB=∠2+∠EAB.
即∠CAB=∠DAE.……………………2分
在△BAC和△DAE中, 4分
∴△BAC≌△DAE(SAS),…………………………………………………………6分
∴BC=DE.……………………………………………………………………………7分
(
A
B
C
(第
2
1
题)
E
F
1
P
)21.(8分)
解:∵ AB=AC,∠C=70°,
∴∠ABC=∠C=70°.…………………………………………………………2分
∵ AB=AC,AE是中线,
∴AE⊥BC,即∠AEB=90°.…………………………………………………………3分
∴∠BAE=90°-70°=20°.…………………………………………………………4分
∵∠ABC=70°,BF是∠ABC的平分线,
∴∠CBF=35°.…………………………………………………………………6分
∵∠1是△BPE的外角,
(
A
B
C
D
(第
22
题)
)∴∠1=90°+35°=125°.……………………………………………………………8分
22.(8分)
∠B=∠C; 1分
AB=AC. 2分
证明:过点A作AD⊥BC,垂足为D. 3分
∵AD⊥BC,
∴∠ADB=∠ADC=90°. 4分
∵ 在△ADB和△ADC中,∠B=∠C,∠ADB=∠ADC,AD=AD, 6分
∴ △ADB≌△ADC(AAS). 7分
(
A
B
C
D
E
G
(第
2
3
题)
)∴AB=AC. 8分
23.(8分)
证明:(1)①连接DE,
∵CE是△ABC的中线,
∴DE是△ABD的中线.
∵AD是高,
∴∠ADB=90°,又DE是△ABD的中线.
∴DE=AB=BE.…………………………………………………………………………2分
∵DC=BE,
∴DC=DE.…………………………………………………………………………4分
∵G是CE的中点,
∴DG⊥CE;…………………………………………………………………………6分
(2)8.……………………………8分
24.(8分)
(1)∵ AB⊥BC,DC⊥BC,
∴ ∠ABC=∠ECD=90°.………………1分
在Rt△ABC和Rt△ECD中,
∴△ABC≌△ECD(HL). ………………2分
(
A
B
C
D
E
F
(第
24
题)
)∴∠DEC=∠CAB.……………3分
∵ ∠ABC=90°,
∴∠CAB+∠BCA=90°.
∴∠DEC+∠BCA=90°.
∴∠EFB=90°.………………………………………………………………………………4分
即AC⊥DE.
(2)连接AE.
∵△ABC≌△ECD,
∴ EC=AB=a,DC=BC=b,DE=AC=c,BE=b-a.
∴ S四边形ABCD=(a+b)b=ab+b2.…………………………………………………5分
∵ AC⊥DE,
∴ S四边形ACBD=S四边形AECD+S△ABE=c2+a(b-a)=c2+ab-a2.……………………6分
∴ab+b2=c2+ab-a2. ………………………7分
即a2+b2=c2. ………………………………………………………………………………8分
25.(8分)
(
C
A
B
A
B
C
A
B
C
①
②
)(1)如图①所示.…………………………………………………………………………4分
(2)法一:如图②所示.………………………………………………………………8分
(
A
B
C
a
) 法二:如图所示.………………………………………………………………8分
法三:如图所示.………………………………………………………………8分
26.(10分)
(1)4. …………………………………………………………………………………2分
(2)证明:如图,∵CD⊥AB.
∴∠CDA=∠CDB=90°,
在Rt△ACD中,由勾股定理得:AD2+DC2=AC2,
∴AC2=12+22=5. ………………………………………………………………………3分
在Rt△BCD中,由勾股定理得:CD2+BD2=BC2,
∴BC2=22+42=20. …………………………4分
在△ACB中,
∵AC2+BC2=5+20=25,
又∵AB2=52=25,
∴AC2+BC2=BC2.…………………………………………………………………………5分
∴由勾股定理逆定理得:△ACB是直角三角形
∴点C是A,B两点的强勾股点.………………………………………………………6分
(3)2,,,8.………………………………………………………10分
(
C
A
B
D
BP
=
2
P
P
C
A
B
D
BP
=
8
C
A
B
D
BP
=
P
C
A
B
D
BP
=
P
)
八年级数学
注意事项:
1.本试卷共6页.全卷满分100分.考试时间为100分钟.考生答题全部答在答题卡上,答在本试卷上无效.
2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.
3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.
一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
1.下面是各届亚运会的会标,其中是轴对称图形的是
A. B. C. D.
2.下列各组数中,是勾股数的是
A.1,2,3 B.2,3,4 C.4,5,6 D.6,8,10
3.如图,用纸板挡住了三角形的一部分,小明根据所学知识重新画出了一个与原来完全一样的三角形,他的依据是
A.AAS B.ASA C.SAS D.SSS
(
(第
3
题)
(第
4
题)
D
B
C
A
E
)
(
(第
5
题)
1
3m
5m
)
4.如图,△ABC≌△ADE,∠B=30°,∠E=100°,∠CAD=20°,则∠BAD的度数为
A.20° B.25° C.30° D.50°
5.下列条件能判断△ABC为等腰三角形的是
A.∠A=40°,∠B=50° C.∠A=40°,∠B=70° B.∠A=40°,∠B=60° D.∠A=40°,∠B=80°
6.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要
A.13m B.17m C.18m D.25m
(
(第
6
题)
13m
5m
A
C
B
(第
8
题)
A
C
B
D
E
F
(第
7
题)
)
7.如图,在Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,E,F分别在边AC,BC上,且AE=CF.下列结论:①DE=DF;②DE⊥DF;③S四边形ECFD=S△ABC.其中所有正确结论的序号是
A.①② B.①③ C.②③ D.①②③
8.如图,在Rt△ABC中,∠C=90°,∠A=20°.若某个三角形与△ABC能拼成一个等腰三角形(无重叠),则拼成的等腰三角形有
A.4种 B.5种 C.6种 D.7种
二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
9.角的对称轴是▲.
10.等腰三角形的顶角为80°,底角的度数为▲°.
(
A
B
C
D
(
第
14
题
)
A
B
C
D
E
(
第
11
题
)
A
C
B
D
O
(
第
15
题
)
)11.如图,AB=AC,用定理“SAS”证明△ABD≌△ACE,还需添加条件:▲.
12.若一个等腰三角形的周长为10,其中一边长为4,则该等腰三角形的腰长为▲.
13.等腰三角形的腰长为5,底边长为6,则底边上的高为▲.
14.如图,在四边形ABCD中,AB⊥BC,AC⊥CD,AC=CD.若AB=3,BC=1,则△ACD 的面积为▲.
15.如图,在△AOC中,以O为圆心,OA为半径画弧,分别交AC,OC于点D,B.若CD=OA,∠O=72°,则∠OAC=▲°.
(
A
B
C
D
E
(
第
16
题
)
O
l
1
l
2
B
C
A
(
第
17
题
)
)16.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.若△ABC的面积为10,AB=6,BC=4,则DE的长为 ▲ .
17.如图,△ABC的边BC,AC的垂直平分线l1,l2相交于点O.若∠A=110°,则∠BOC=▲°.
18.在△ABC中,∠A=30°,AB=2.若对于BC的每一个值,对应的△ABC的形状、大小都唯一确定,则BC长的取值范围是▲.
三、解答题(本大题共8小题,共64分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(7分)如图,在边长为1个单位长度的小正方形组成的网格中,点A,B在小正方形的顶点上.
(1)在图中画出与线段AB关于直线l成轴对称的线段A′B′;
(2)在直线l上确定一点P,使PA+PB最短.
(
A
B
l
(第
19
题)
)
(
(第
20
题)
A
C
1
2
B
E
)20.(7分)如图,AC=AE,∠1=∠2,AB=AD.求证BC=DE.
(
D
)
21.(8分)如图,在△ABC中,AB=AC,AE是中线,BF是角平分线,∠C=70°.
(
A
B
C
(第
2
1
题)
E
F
1
)求∠BAE和∠1的度数.
22.(8分)证明:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
(
A
B
C
(第
22
题)
)已知:如图,在△ABC中,▲.
求证:▲.
证明:
23.(8分)如图,在△ABC中,AD是高,CE是中线,且DC=BE,G是CE的中点.
(1)求证DG⊥CE;
(
A
B
C
D
E
G
(第
2
3
题)
)(2)若AB=AC,DG=2,则AB的长为▲.
24.(8分)如图,AB⊥BC,DC⊥BC,垂足分别为B,C,DE交BC于点E,AB=EC,AC=DE.
(1)求证AC⊥DE;
(
A
B
C
D
E
(第
24
题)
)(2)连接AD,若AB=a,BC=b,AC=c,通过用不同方法计算四边形ABCD的面积,验证勾股定理.
25.(8分)如图,已知线段a和∠MAN.在边AM上作点B,在边AN上作点C,分别满足下列条件:
(1)在图①中,AB=a,AC=BC;
(2)在图②中,BC=a,AB=AC.
(要求:用直尺和圆规作图,保留作图痕迹,写出必要的文字说明).
(
a
A
N
M
A
N
M
①
②
)
26.(10分)
【概念认识】
定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.当这个点是直角的顶点时,这个点又称为强勾股点.
(
C
A
B
①
)如图①,在Rt△ABC中,∠C=90°,A是B,C两点的勾股点,B是A,C两点的勾股点,C是A,B两点的勾股点,也是强勾股点.
(
②
A
B
C
D
)
【概念运用】
(1)如图②,方格纸中的每个小正方形的边长均为1,A,B两点均在格点上,线段CD上的8个格点中,是A,B两点的勾股点的有▲个.
(
C
A
B
D
③
)(2)如图③,在△ABC中,CD⊥AB,垂足为D,若AD=1,BD=4,CD=2.
(
C
A
B
D
)求证:C是A,B两点的强勾股点.
【拓展提升】
(
C
A
B
D
④
)(3)如图④,在Rt△ABC中,∠C=90°,AC=6,BC=4,D是AC的中点,P是射线BD上一个动点,当P是Rt△ABC任意两个顶点的强勾股点时,直接写出BP的长.
2023-2024学年度第一学期期中学情分析样题
八年级数学参考答案
说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.
一、选择题 (本大题共8小题,每小题2分,共16分)
题号 1 2 3 4 5 6 7 8
答案 C D B C C B D D
二、填空题 (本大题共10小题,每小题2分,共20分)
9.角平分线所在的直线 10.50° 11.AE=AD 12.3或4 13.4
(
C
A
B
l
(第
19
题)
A'
B
'
P
)14.5 15.72° 16.2 17.140° 18.BC=1或BC≥2
三、解答题(本大题共8小题,共64分)
19.(7分)
(1)画对A′B′;……………………4分
(2)画对点P.……………………7分
20.(7分)
证明:∵∠1=∠2,
(
D
(第
20
题)
A
C
1
2
E
)∴∠1+∠EAB=∠2+∠EAB.
即∠CAB=∠DAE.……………………2分
在△BAC和△DAE中, 4分
∴△BAC≌△DAE(SAS),…………………………………………………………6分
∴BC=DE.……………………………………………………………………………7分
(
A
B
C
(第
2
1
题)
E
F
1
P
)21.(8分)
解:∵ AB=AC,∠C=70°,
∴∠ABC=∠C=70°.…………………………………………………………2分
∵ AB=AC,AE是中线,
∴AE⊥BC,即∠AEB=90°.…………………………………………………………3分
∴∠BAE=90°-70°=20°.…………………………………………………………4分
∵∠ABC=70°,BF是∠ABC的平分线,
∴∠CBF=35°.…………………………………………………………………6分
∵∠1是△BPE的外角,
(
A
B
C
D
(第
22
题)
)∴∠1=90°+35°=125°.……………………………………………………………8分
22.(8分)
∠B=∠C; 1分
AB=AC. 2分
证明:过点A作AD⊥BC,垂足为D. 3分
∵AD⊥BC,
∴∠ADB=∠ADC=90°. 4分
∵ 在△ADB和△ADC中,∠B=∠C,∠ADB=∠ADC,AD=AD, 6分
∴ △ADB≌△ADC(AAS). 7分
(
A
B
C
D
E
G
(第
2
3
题)
)∴AB=AC. 8分
23.(8分)
证明:(1)①连接DE,
∵CE是△ABC的中线,
∴DE是△ABD的中线.
∵AD是高,
∴∠ADB=90°,又DE是△ABD的中线.
∴DE=AB=BE.…………………………………………………………………………2分
∵DC=BE,
∴DC=DE.…………………………………………………………………………4分
∵G是CE的中点,
∴DG⊥CE;…………………………………………………………………………6分
(2)8.……………………………8分
24.(8分)
(1)∵ AB⊥BC,DC⊥BC,
∴ ∠ABC=∠ECD=90°.………………1分
在Rt△ABC和Rt△ECD中,
∴△ABC≌△ECD(HL). ………………2分
(
A
B
C
D
E
F
(第
24
题)
)∴∠DEC=∠CAB.……………3分
∵ ∠ABC=90°,
∴∠CAB+∠BCA=90°.
∴∠DEC+∠BCA=90°.
∴∠EFB=90°.………………………………………………………………………………4分
即AC⊥DE.
(2)连接AE.
∵△ABC≌△ECD,
∴ EC=AB=a,DC=BC=b,DE=AC=c,BE=b-a.
∴ S四边形ABCD=(a+b)b=ab+b2.…………………………………………………5分
∵ AC⊥DE,
∴ S四边形ACBD=S四边形AECD+S△ABE=c2+a(b-a)=c2+ab-a2.……………………6分
∴ab+b2=c2+ab-a2. ………………………7分
即a2+b2=c2. ………………………………………………………………………………8分
25.(8分)
(
C
A
B
A
B
C
A
B
C
①
②
)(1)如图①所示.…………………………………………………………………………4分
(2)法一:如图②所示.………………………………………………………………8分
(
A
B
C
a
) 法二:如图所示.………………………………………………………………8分
法三:如图所示.………………………………………………………………8分
26.(10分)
(1)4. …………………………………………………………………………………2分
(2)证明:如图,∵CD⊥AB.
∴∠CDA=∠CDB=90°,
在Rt△ACD中,由勾股定理得:AD2+DC2=AC2,
∴AC2=12+22=5. ………………………………………………………………………3分
在Rt△BCD中,由勾股定理得:CD2+BD2=BC2,
∴BC2=22+42=20. …………………………4分
在△ACB中,
∵AC2+BC2=5+20=25,
又∵AB2=52=25,
∴AC2+BC2=BC2.…………………………………………………………………………5分
∴由勾股定理逆定理得:△ACB是直角三角形
∴点C是A,B两点的强勾股点.………………………………………………………6分
(3)2,,,8.………………………………………………………10分
(
C
A
B
D
BP
=
2
P
P
C
A
B
D
BP
=
8
C
A
B
D
BP
=
P
C
A
B
D
BP
=
P
)
同课章节目录
