7.5 三角形内角和定理分层练习(含答案)
文档属性
| 名称 | 7.5 三角形内角和定理分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 806.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
7.5三角形内角和定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
A.120° B.80° C.60° D.40°
2.在三角形中,最大的内角不小于( )
A.30° B.45° C.60° D.90°
3.的,,则( )
A. B. C. D.
4.在中,,分别平分和,若,则等于( )
A. B. C. D.
5.如图,在中,,则( )
A. B. C. D.
6.光线a照射到平面镜上,然后在平面镜和之间来回反射.若已知,则( )
A. B. C. D.
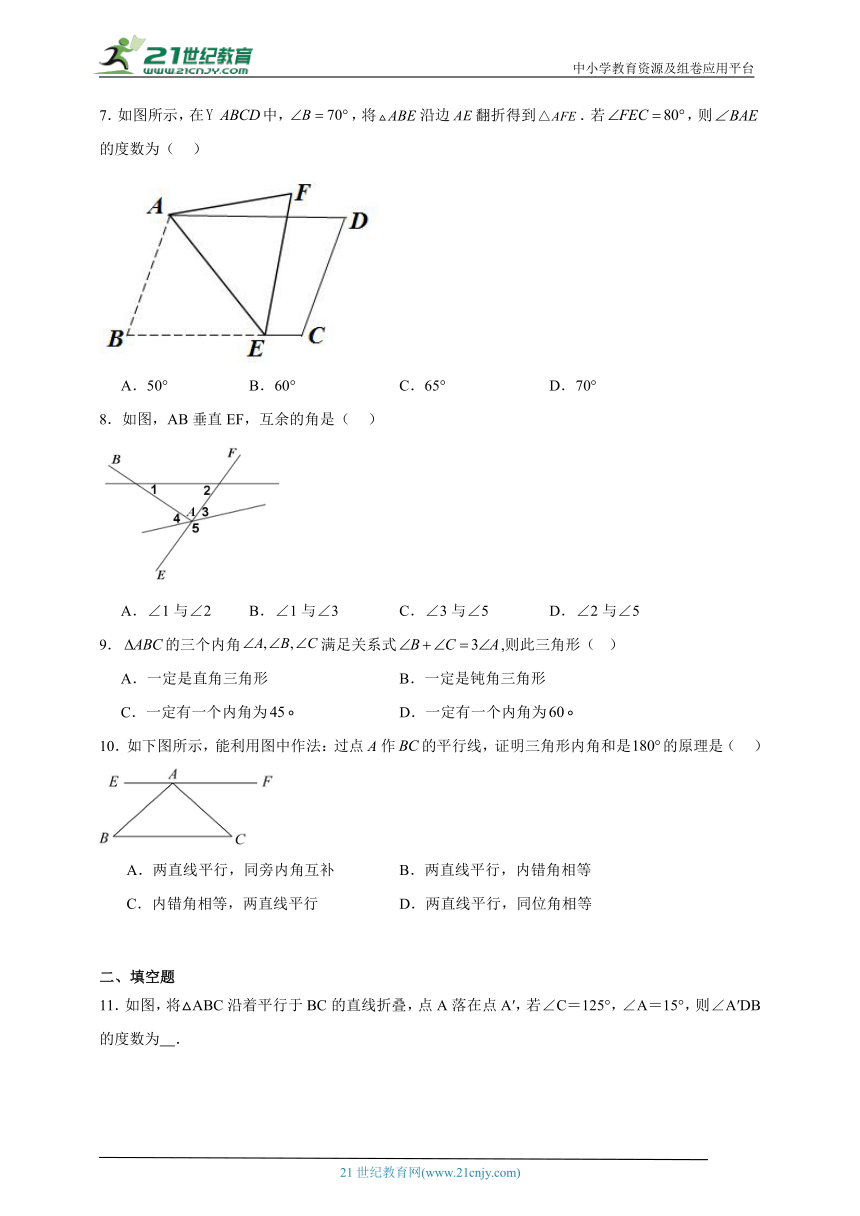
7.如图所示,在中,,将沿边翻折得到.若,则的度数为( )
A.50° B.60° C.65° D.70°
8.如图,AB垂直EF,互余的角是( )
A.∠1与∠2 B.∠1与∠3 C.∠3与∠5 D.∠2与∠5
9.的三个内角满足关系式,则此三角形( )
A.一定是直角三角形 B.一定是钝角三角形
C.一定有一个内角为 D.一定有一个内角为
10.如下图所示,能利用图中作法:过点A作的平行线,证明三角形内角和是的原理是( )
A.两直线平行,同旁内角互补 B.两直线平行,内错角相等
C.内错角相等,两直线平行 D.两直线平行,同位角相等
二、填空题
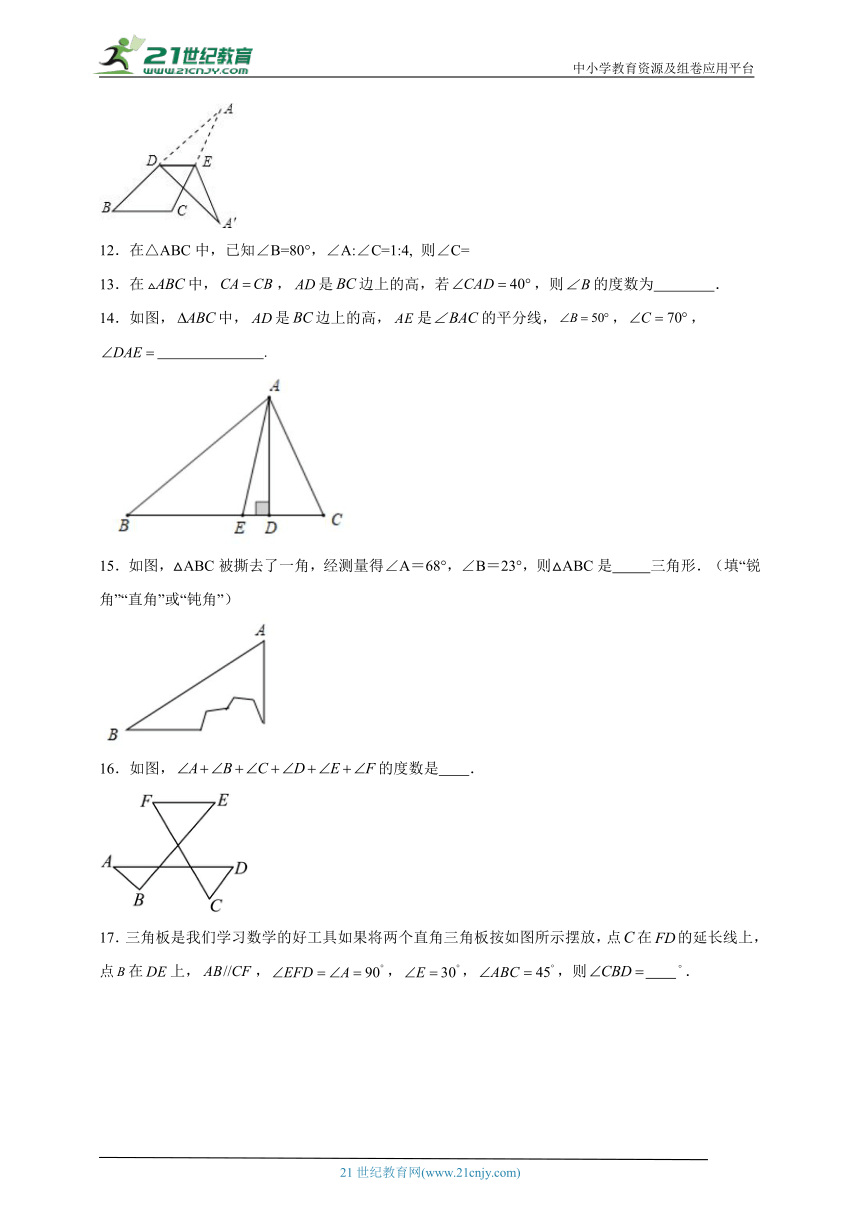
11.如图,将△ABC沿着平行于BC的直线折叠,点A落在点A′,若∠C=125°,∠A=15°,则∠A′DB的度数为 .
12.在△ABC中,已知∠B=80°,∠A:∠C=1:4, 则∠C=
13.在中,,是边上的高,若,则的度数为 .
14.如图,中,是边上的高,是的平分线,,, .
15.如图,△ABC被撕去了一角,经测量得∠A=68°,∠B=23°,则△ABC是 三角形.(填“锐角”“直角”或“钝角”)
16.如图,的度数是 .
17.三角板是我们学习数学的好工具如果将两个直角三角板按如图所示摆放,点在的延长线上,点在上,,,,,则 .
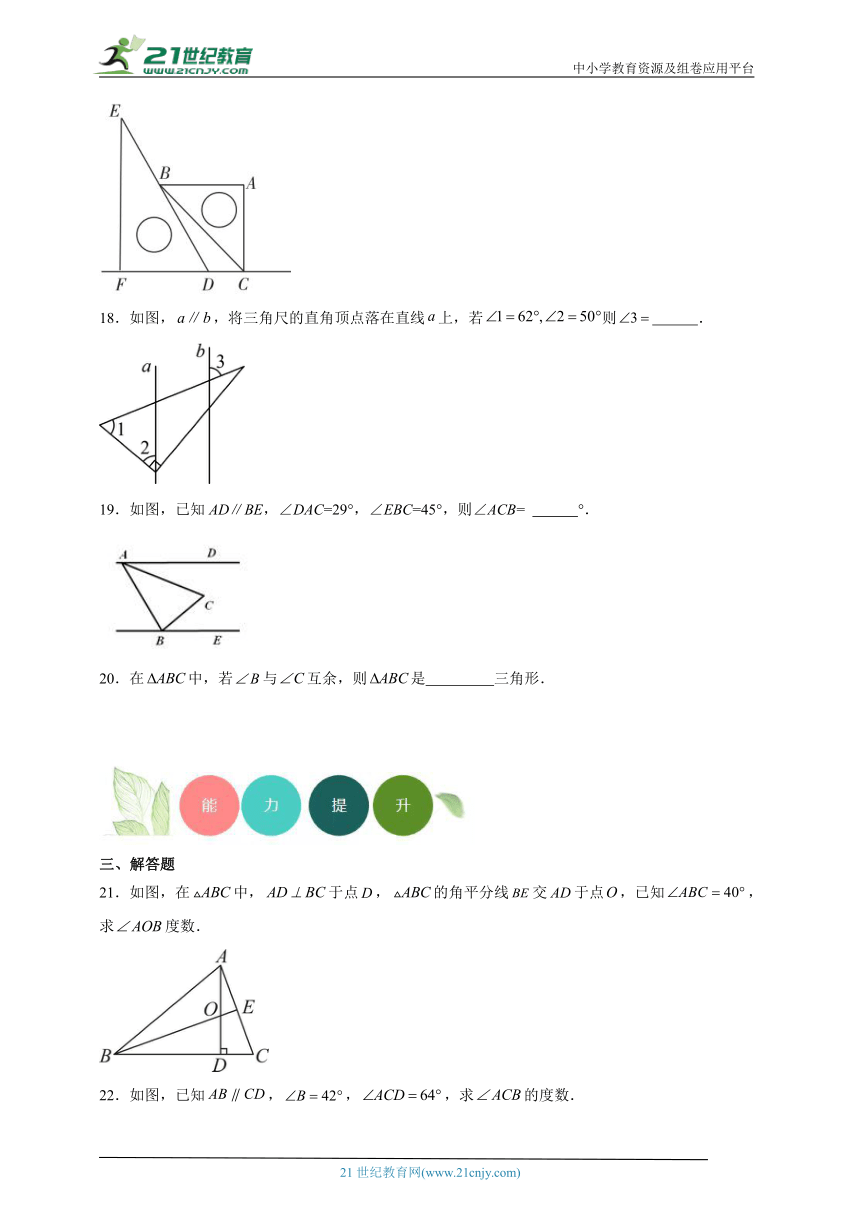
18.如图,,将三角尺的直角顶点落在直线上,若则 .
19.如图,已知AD∥BE,∠DAC=29°,∠EBC=45°,则∠ACB= °.
20.在中,若与互余,则是 三角形.
三、解答题
21.如图,在中,于点,的角平分线交于点,已知,求度数.
22.如图,已知,,,求的度数.
23.如图1,在平面直角坐标系中,的三个顶点为,,,且满足,线段交轴于点,,点是轴负半轴.上一动点(点不与点重合).
(1)求点、、的坐标.
(2)问题探究:
①如图2,过点作,小明发现在点的运动过程中,的度数为定值,为求出这个定值,小明过点作,请你帮他用表示出的度数,并说明理由;
②如图3,分别作,的平分线交于点,试问在点的运动过程中,的度数是否发生变化,若变化,请说明理由,若不变,请求出的度数.
24.如图,已知直线与直线、分别相交于点、,点是位于下方,上方,右侧的一点,.
(1)求证:;
(2)若,分别平分,,请在图1中画出点,并连接,.判断与是否垂直,并说明理由(不要求尺规作图);
(3)如图2,过点作垂直于直线,交于点,点是射线上一点,连接,,,作的角平分线,交于点,点是的邻补角平分线上一点,连接,若,试判断射线上是否存在一点,有,说明理由.
25.已知,如图,,直线交于点,交于点,点是线段上一点,,分别在射线,上,连接,,平分,平分.
(1)如图1,当时,直接写出的度数;
(2)如图2,求与之间的数量关系,并说明理由;
(3)如图3,在(1)问的条件下,若,,过点P作交的延长线于点,将绕点顺时针旋转,速度为每秒,直线旋转后的对应直线为,同时绕点P逆时针旋转,速度为每秒,旋转后的对应三角形为,当首次落到上时,整个运动停止,在此运动过程中,经过秒后,恰好平行于的其中一条边,请直接写出所有满足条件的t的值,并选择其中一种情况书写计算过程.
参考答案:
1.C
2.C
3.A
4.C
5.C
6.D
7.B
8.A
9.C
10.B
11.100°/100度
12.80°
13.或
14.
15.锐角
16.360°/360度
17.15
18./68度
19.74
20.直角
21.
22.
23.(1)A,B,C
(2)①②的度数不发生变化,
24.(1)略
(2)垂直
(3)不存在
25.(1)
(2)
(3)或6.5或12.5或16.5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.5三角形内角和定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
A.120° B.80° C.60° D.40°
2.在三角形中,最大的内角不小于( )
A.30° B.45° C.60° D.90°
3.的,,则( )
A. B. C. D.
4.在中,,分别平分和,若,则等于( )
A. B. C. D.
5.如图,在中,,则( )
A. B. C. D.
6.光线a照射到平面镜上,然后在平面镜和之间来回反射.若已知,则( )
A. B. C. D.
7.如图所示,在中,,将沿边翻折得到.若,则的度数为( )
A.50° B.60° C.65° D.70°
8.如图,AB垂直EF,互余的角是( )
A.∠1与∠2 B.∠1与∠3 C.∠3与∠5 D.∠2与∠5
9.的三个内角满足关系式,则此三角形( )
A.一定是直角三角形 B.一定是钝角三角形
C.一定有一个内角为 D.一定有一个内角为
10.如下图所示,能利用图中作法:过点A作的平行线,证明三角形内角和是的原理是( )
A.两直线平行,同旁内角互补 B.两直线平行,内错角相等
C.内错角相等,两直线平行 D.两直线平行,同位角相等
二、填空题
11.如图,将△ABC沿着平行于BC的直线折叠,点A落在点A′,若∠C=125°,∠A=15°,则∠A′DB的度数为 .
12.在△ABC中,已知∠B=80°,∠A:∠C=1:4, 则∠C=
13.在中,,是边上的高,若,则的度数为 .
14.如图,中,是边上的高,是的平分线,,, .
15.如图,△ABC被撕去了一角,经测量得∠A=68°,∠B=23°,则△ABC是 三角形.(填“锐角”“直角”或“钝角”)
16.如图,的度数是 .
17.三角板是我们学习数学的好工具如果将两个直角三角板按如图所示摆放,点在的延长线上,点在上,,,,,则 .
18.如图,,将三角尺的直角顶点落在直线上,若则 .
19.如图,已知AD∥BE,∠DAC=29°,∠EBC=45°,则∠ACB= °.
20.在中,若与互余,则是 三角形.
三、解答题
21.如图,在中,于点,的角平分线交于点,已知,求度数.
22.如图,已知,,,求的度数.
23.如图1,在平面直角坐标系中,的三个顶点为,,,且满足,线段交轴于点,,点是轴负半轴.上一动点(点不与点重合).
(1)求点、、的坐标.
(2)问题探究:
①如图2,过点作,小明发现在点的运动过程中,的度数为定值,为求出这个定值,小明过点作,请你帮他用表示出的度数,并说明理由;
②如图3,分别作,的平分线交于点,试问在点的运动过程中,的度数是否发生变化,若变化,请说明理由,若不变,请求出的度数.
24.如图,已知直线与直线、分别相交于点、,点是位于下方,上方,右侧的一点,.
(1)求证:;
(2)若,分别平分,,请在图1中画出点,并连接,.判断与是否垂直,并说明理由(不要求尺规作图);
(3)如图2,过点作垂直于直线,交于点,点是射线上一点,连接,,,作的角平分线,交于点,点是的邻补角平分线上一点,连接,若,试判断射线上是否存在一点,有,说明理由.
25.已知,如图,,直线交于点,交于点,点是线段上一点,,分别在射线,上,连接,,平分,平分.
(1)如图1,当时,直接写出的度数;
(2)如图2,求与之间的数量关系,并说明理由;
(3)如图3,在(1)问的条件下,若,,过点P作交的延长线于点,将绕点顺时针旋转,速度为每秒,直线旋转后的对应直线为,同时绕点P逆时针旋转,速度为每秒,旋转后的对应三角形为,当首次落到上时,整个运动停止,在此运动过程中,经过秒后,恰好平行于的其中一条边,请直接写出所有满足条件的t的值,并选择其中一种情况书写计算过程.
参考答案:
1.C
2.C
3.A
4.C
5.C
6.D
7.B
8.A
9.C
10.B
11.100°/100度
12.80°
13.或
14.
15.锐角
16.360°/360度
17.15
18./68度
19.74
20.直角
21.
22.
23.(1)A,B,C
(2)①②的度数不发生变化,
24.(1)略
(2)垂直
(3)不存在
25.(1)
(2)
(3)或6.5或12.5或16.5
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
