6.4 数据的离散程度分层练习(含答案)
文档属性
| 名称 | 6.4 数据的离散程度分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 697.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 21:10:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.4数据的离散程度
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为了解“五项管理”之“睡眠管理”的落实情况,教育局在某初中学校随机调查了60名学生每天的睡眠时间(小时),将样本数据绘制成如下统计表,其中有两个数据不慎被污渍遮盖,下列关于睡眠时间的统计量中,不受被遮盖的数据影响的是( )
睡眠时间/小时 7 8 9 10 11
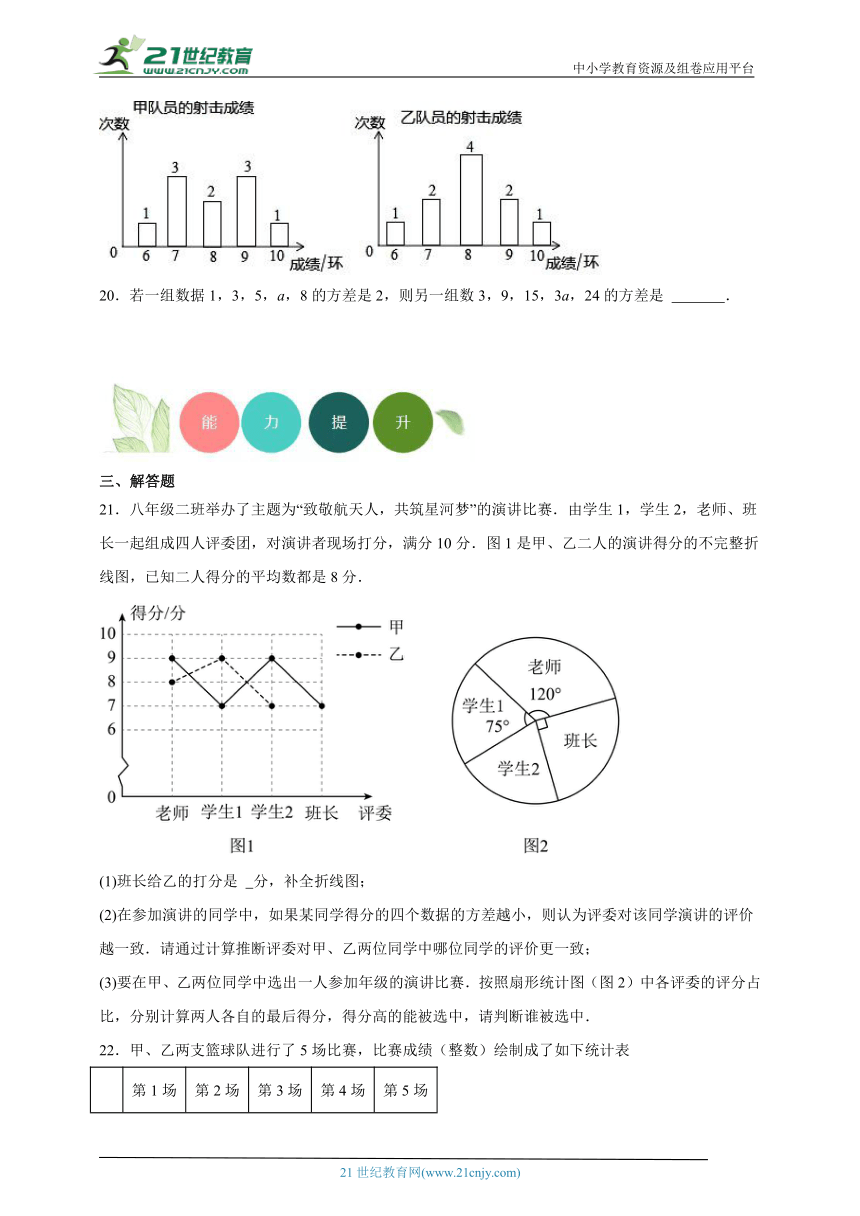
人数/人 2 6 25
A.平均数 B.中位数 C.众数 D.方差
2.某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,得到两个品种的平均产量相同,且方差分别为,,则( )
A.甲的产量稳定 B.乙的产量稳定
C.甲、乙的产量一样稳定 D.无法确定哪一品种的产量更稳定
3.2020年9月28日上午,2020中国企业500强榜单在郑州发布,本次河南共有10家企业上榜2020中国企业500强,18家企业上榜制造业企业500强,7家企业上榜服务业企业500强,上榜企业数较上年均有所增加.郑州某企业1~5月份利润的变化情况如图所示,则以下说法与图中反映的信息相符的是( )
A.1~2月份利润的增长快于2~3月份利润的增长
B.1~4月份利润的极差与1~5月份利润的极差不同
C.1~5月份利润的众数是130万元
D.1~5月份利润的中位数为120万元
4.一组数据1,2,2,3,5,将这组数据中的每一个数都加上,得到一组新数据,,,,,这两组数据的以下统计量相等的是( )
A.平均数 B.众数 C.中位数 D.方差
5.体育老师对亮亮和薇薇两名同学的立定跳远进行了五次测试(满分为10分),把他们的成绩绘制成如下统计图.根据图中信息,下列说法正确的是( )
A.亮亮的跳远成绩比薇薇的跳远成绩稳定
B.亮亮的成绩越来越好,如果再跳一次一定还是10分
C.亮亮的第三次成绩与第二次成绩相比,增长率超过
D.亮亮和薇薇的成绩都在8分上下波动,两个人的成绩稳定性一样
6.某班45名同学某天每人的生活费用统计如表:
对于这45名同学这天每人的生活费用,下列说法错误的是( )
A.平均数是20 B.众数是20 C.中位数是20 D.极差是20
7.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差是1.8.下列说法中不一定正确的是( )
A.甲、乙射中的总环数相同 B.甲的成绩稳定 C.乙的成绩波动较大 D.甲、乙的众数相同
8.甲、乙两组数据,它们都是由n个数据组成,甲组数据的方差是0.4,乙组数据的方差是0.2,那么下列关于甲乙两组数据波动说法正确的是( ).
A.甲的波动小 B.乙的波动小 C.甲、乙的波动相同 D.甲、乙的波动的大小无法比较
9.一组数据1,1,1,3,4,7,12,若加入一个整数,一定不会发生变化的统计量是( )
A.众数 B.平均数 C.中位数 D.方差
10.明明在对一组数据:9,1■,25,25,进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.众数 B.中位数 C.平均数 D.方差
二、填空题
11.数据-1,0,2,4,3的极差是 .
12.为参加校运会,小强同学进行立定跳远训练,其中6次的成绩如下(单位:):2.2,2.6,2.4,2.5,2.4,2.4,这6次成绩的极差是 .
13.若另一组数据的标准差是2,则方差是 .
14.在三次体育加试预测中,甲、乙两名同学的平均分都是47.5分,方差分别是,,则成绩较稳定的同学是 .
15.信阳是全国有名的板栗之乡,板栗年产量达数百万千克.某农场准备从甲、乙、丙三个品种的板栗树中选出一种产量既高又稳定的板栗树进行种植,现随机从这三个品种的板栗树中各选10棵,每棵产量的平均数(单位:千克)及方差如下表所示.该农场应选的品种
是
甲 乙 丙
43 43 41
1.2 1.1 1.2
16.在分析数据时,小明列出方差的计算公式.则这列数据的中位数是 .
17.甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:s甲2=2,s乙2=4,则射击成绩较稳定的是 (选填“甲”或“乙”).
18.近日,生态环境部公布第六批“绿水青山就是金山银山”实践创新基地名单,山西省6个县入选国家生态文明建设示范区,为了响应对环境保护的号召,某校要从报名的甲、乙、丙三人中选取一人去参加太原市举办的环保演讲比赛,经过两轮初赛后,甲、乙、丙三人的平均成绩都是90,方差分别是,,.你认为 参加决赛比较合适.
19.已知甲、乙两队员射击的成绩如图,设甲、乙两队员射击成绩的方差分别为S甲2、S乙2,则S甲2 S乙2(填“>”、“=”、“<”).
20.若一组数据1,3,5,a,8的方差是2,则另一组数3,9,15,3a,24的方差是 .
三、解答题
21.八年级二班举办了主题为“致敬航天人,共筑星河梦”的演讲比赛.由学生1,学生2,老师、班长一起组成四人评委团,对演讲者现场打分,满分10分.图1是甲、乙二人的演讲得分的不完整折线图,已知二人得分的平均数都是8分.
(1)班长给乙的打分是 分,补全折线图;
(2)在参加演讲的同学中,如果某同学得分的四个数据的方差越小,则认为评委对该同学演讲的评价越一致.请通过计算推断评委对甲、乙两位同学中哪位同学的评价更一致;
(3)要在甲、乙两位同学中选出一人参加年级的演讲比赛.按照扇形统计图(图2)中各评委的评分占比,分别计算两人各自的最后得分,得分高的能被选中,请判断谁被选中.
22.甲、乙两支篮球队进行了5场比赛,比赛成绩(整数)绘制成了如下统计表
第1场 第2场 第3场 第4场 第5场
甲
乙
(1)填写下表:
平均数 中位数 方差
甲 ______ ______
乙 ______
(2)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更有可能取得好成绩?
23.甲、乙两名队员练习射击,每次射击的环数为整数,两人各射击10次,其成绩分别绘制成如图1、图2所示的统计图,两幅图均有部分被污染,两名队员10次的射击成绩整理后,得到的统计表如下表所示.
平均数 中位数 众数 方差
甲 a 7 b 1.8
乙 7 c 8 3
(1)甲队员射中7环的次数为___________;
(2)统计表中___________;___________;___________;
(3)___________队员的发挥更稳定;
(4)乙队员补射1次后,成绩为m环,据统计乙队员这11次射击成绩的中位数比c大0.5,则m的最小值为___________.
24.某研究所甲、乙试验田各有水稻穗4万个,为了考察水稻穗长的情况,研究员于同一天在这两块试验田里分别随机抽取了50个稻穗进行测量,获得了它们的长度(单位:),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如表1所示(不完整):
b.乙试验田穗长的频数分布直方图如图1所示:
甲试验田穗长频数分布表
分组 频数 频率
4 0.08
9 0.18
11 0.22
0.20
2
合计 50 1.00
c.乙试验田穗长在这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 平均数 中位数 众数 方差
甲 5.924 5.8 5.8 0.454
乙 5.924 6.5 0.608
根据以上信息,回答下列问题:
(1)表1中的值为 ,的值为 ;
(2)表2中的值为 :
(3)根据考察的结果,将稻穗按穗长从长到短进行排序后,穗长为的稻穗的穗长排名更靠前的试验田是 ,穗长较稳定的试验田是
(4)若穗长在范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 个.
参考答案:
1.B
2.A
3.C
4.D
5.C
6.A
7.D
8.B
9.A
10.A
11.5.
12./
13.4
14.乙
15.乙
16.
17.甲
18.甲
19.>
20.18
21.(1)8
(2)评委对乙同学的评价更一致
(3)甲
22.(1),,
(2)略
23.(1)4
(2)7,7,7.5
(3)甲
(4)8
24.(1)14,10
(2)
(3)甲,甲
(4)万
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.4数据的离散程度
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为了解“五项管理”之“睡眠管理”的落实情况,教育局在某初中学校随机调查了60名学生每天的睡眠时间(小时),将样本数据绘制成如下统计表,其中有两个数据不慎被污渍遮盖,下列关于睡眠时间的统计量中,不受被遮盖的数据影响的是( )
睡眠时间/小时 7 8 9 10 11
人数/人 2 6 25
A.平均数 B.中位数 C.众数 D.方差
2.某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,得到两个品种的平均产量相同,且方差分别为,,则( )
A.甲的产量稳定 B.乙的产量稳定
C.甲、乙的产量一样稳定 D.无法确定哪一品种的产量更稳定
3.2020年9月28日上午,2020中国企业500强榜单在郑州发布,本次河南共有10家企业上榜2020中国企业500强,18家企业上榜制造业企业500强,7家企业上榜服务业企业500强,上榜企业数较上年均有所增加.郑州某企业1~5月份利润的变化情况如图所示,则以下说法与图中反映的信息相符的是( )
A.1~2月份利润的增长快于2~3月份利润的增长
B.1~4月份利润的极差与1~5月份利润的极差不同
C.1~5月份利润的众数是130万元
D.1~5月份利润的中位数为120万元
4.一组数据1,2,2,3,5,将这组数据中的每一个数都加上,得到一组新数据,,,,,这两组数据的以下统计量相等的是( )
A.平均数 B.众数 C.中位数 D.方差
5.体育老师对亮亮和薇薇两名同学的立定跳远进行了五次测试(满分为10分),把他们的成绩绘制成如下统计图.根据图中信息,下列说法正确的是( )
A.亮亮的跳远成绩比薇薇的跳远成绩稳定
B.亮亮的成绩越来越好,如果再跳一次一定还是10分
C.亮亮的第三次成绩与第二次成绩相比,增长率超过
D.亮亮和薇薇的成绩都在8分上下波动,两个人的成绩稳定性一样
6.某班45名同学某天每人的生活费用统计如表:
对于这45名同学这天每人的生活费用,下列说法错误的是( )
A.平均数是20 B.众数是20 C.中位数是20 D.极差是20
7.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差是1.8.下列说法中不一定正确的是( )
A.甲、乙射中的总环数相同 B.甲的成绩稳定 C.乙的成绩波动较大 D.甲、乙的众数相同
8.甲、乙两组数据,它们都是由n个数据组成,甲组数据的方差是0.4,乙组数据的方差是0.2,那么下列关于甲乙两组数据波动说法正确的是( ).
A.甲的波动小 B.乙的波动小 C.甲、乙的波动相同 D.甲、乙的波动的大小无法比较
9.一组数据1,1,1,3,4,7,12,若加入一个整数,一定不会发生变化的统计量是( )
A.众数 B.平均数 C.中位数 D.方差
10.明明在对一组数据:9,1■,25,25,进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.众数 B.中位数 C.平均数 D.方差
二、填空题
11.数据-1,0,2,4,3的极差是 .
12.为参加校运会,小强同学进行立定跳远训练,其中6次的成绩如下(单位:):2.2,2.6,2.4,2.5,2.4,2.4,这6次成绩的极差是 .
13.若另一组数据的标准差是2,则方差是 .
14.在三次体育加试预测中,甲、乙两名同学的平均分都是47.5分,方差分别是,,则成绩较稳定的同学是 .
15.信阳是全国有名的板栗之乡,板栗年产量达数百万千克.某农场准备从甲、乙、丙三个品种的板栗树中选出一种产量既高又稳定的板栗树进行种植,现随机从这三个品种的板栗树中各选10棵,每棵产量的平均数(单位:千克)及方差如下表所示.该农场应选的品种
是
甲 乙 丙
43 43 41
1.2 1.1 1.2
16.在分析数据时,小明列出方差的计算公式.则这列数据的中位数是 .
17.甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:s甲2=2,s乙2=4,则射击成绩较稳定的是 (选填“甲”或“乙”).
18.近日,生态环境部公布第六批“绿水青山就是金山银山”实践创新基地名单,山西省6个县入选国家生态文明建设示范区,为了响应对环境保护的号召,某校要从报名的甲、乙、丙三人中选取一人去参加太原市举办的环保演讲比赛,经过两轮初赛后,甲、乙、丙三人的平均成绩都是90,方差分别是,,.你认为 参加决赛比较合适.
19.已知甲、乙两队员射击的成绩如图,设甲、乙两队员射击成绩的方差分别为S甲2、S乙2,则S甲2 S乙2(填“>”、“=”、“<”).
20.若一组数据1,3,5,a,8的方差是2,则另一组数3,9,15,3a,24的方差是 .
三、解答题
21.八年级二班举办了主题为“致敬航天人,共筑星河梦”的演讲比赛.由学生1,学生2,老师、班长一起组成四人评委团,对演讲者现场打分,满分10分.图1是甲、乙二人的演讲得分的不完整折线图,已知二人得分的平均数都是8分.
(1)班长给乙的打分是 分,补全折线图;
(2)在参加演讲的同学中,如果某同学得分的四个数据的方差越小,则认为评委对该同学演讲的评价越一致.请通过计算推断评委对甲、乙两位同学中哪位同学的评价更一致;
(3)要在甲、乙两位同学中选出一人参加年级的演讲比赛.按照扇形统计图(图2)中各评委的评分占比,分别计算两人各自的最后得分,得分高的能被选中,请判断谁被选中.
22.甲、乙两支篮球队进行了5场比赛,比赛成绩(整数)绘制成了如下统计表
第1场 第2场 第3场 第4场 第5场
甲
乙
(1)填写下表:
平均数 中位数 方差
甲 ______ ______
乙 ______
(2)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更有可能取得好成绩?
23.甲、乙两名队员练习射击,每次射击的环数为整数,两人各射击10次,其成绩分别绘制成如图1、图2所示的统计图,两幅图均有部分被污染,两名队员10次的射击成绩整理后,得到的统计表如下表所示.
平均数 中位数 众数 方差
甲 a 7 b 1.8
乙 7 c 8 3
(1)甲队员射中7环的次数为___________;
(2)统计表中___________;___________;___________;
(3)___________队员的发挥更稳定;
(4)乙队员补射1次后,成绩为m环,据统计乙队员这11次射击成绩的中位数比c大0.5,则m的最小值为___________.
24.某研究所甲、乙试验田各有水稻穗4万个,为了考察水稻穗长的情况,研究员于同一天在这两块试验田里分别随机抽取了50个稻穗进行测量,获得了它们的长度(单位:),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如表1所示(不完整):
b.乙试验田穗长的频数分布直方图如图1所示:
甲试验田穗长频数分布表
分组 频数 频率
4 0.08
9 0.18
11 0.22
0.20
2
合计 50 1.00
c.乙试验田穗长在这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 平均数 中位数 众数 方差
甲 5.924 5.8 5.8 0.454
乙 5.924 6.5 0.608
根据以上信息,回答下列问题:
(1)表1中的值为 ,的值为 ;
(2)表2中的值为 :
(3)根据考察的结果,将稻穗按穗长从长到短进行排序后,穗长为的稻穗的穗长排名更靠前的试验田是 ,穗长较稳定的试验田是
(4)若穗长在范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 个.
参考答案:
1.B
2.A
3.C
4.D
5.C
6.A
7.D
8.B
9.A
10.A
11.5.
12./
13.4
14.乙
15.乙
16.
17.甲
18.甲
19.>
20.18
21.(1)8
(2)评委对乙同学的评价更一致
(3)甲
22.(1),,
(2)略
23.(1)4
(2)7,7,7.5
(3)甲
(4)8
24.(1)14,10
(2)
(3)甲,甲
(4)万
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
