18.2.1矩形
图片预览





文档简介
课件33张PPT。18.2 特殊的平行四边形 18.2.1 矩形
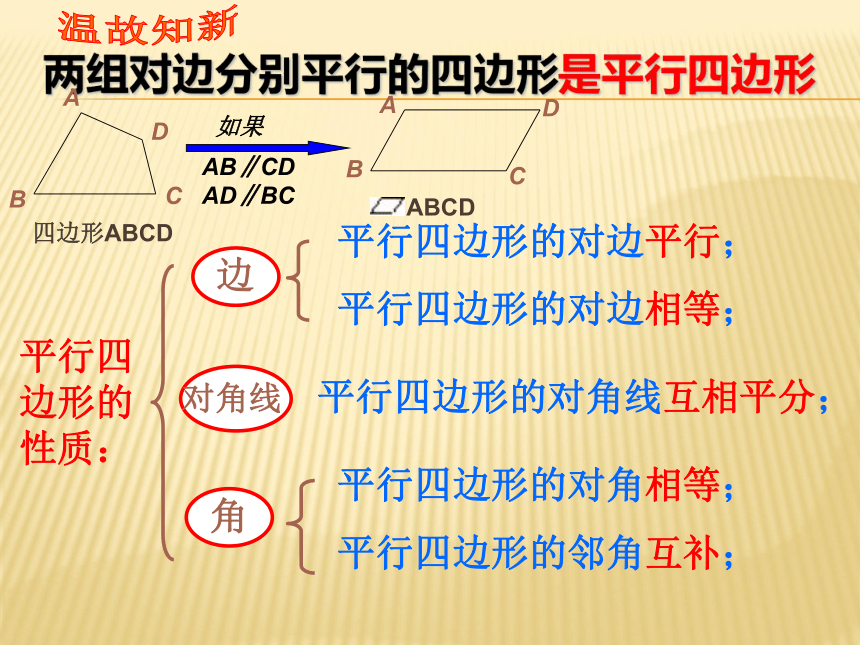
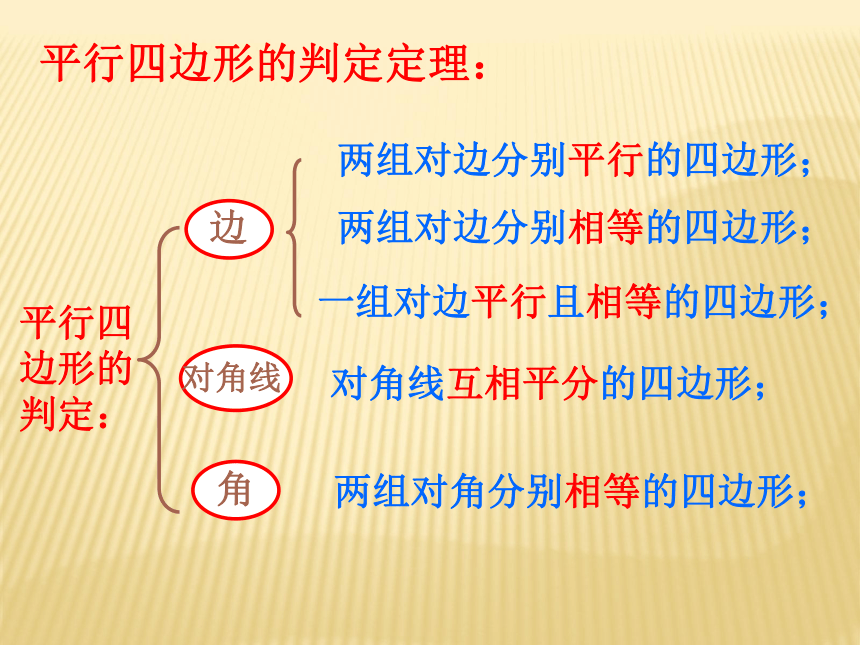
第一课时 两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理:一个角是
直角两组对边
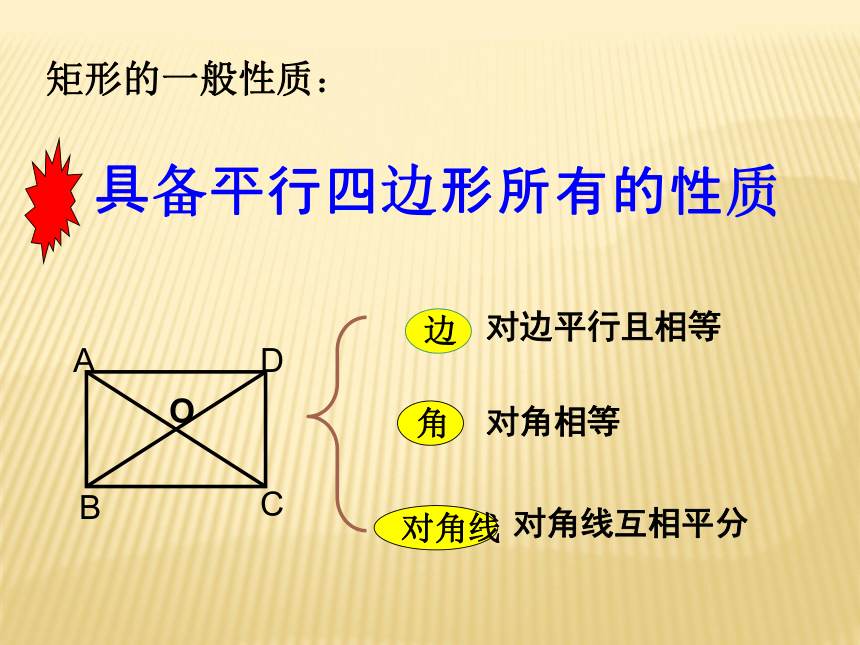
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形—— 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等对角线互相平分矩形的一般性质:探索新知:
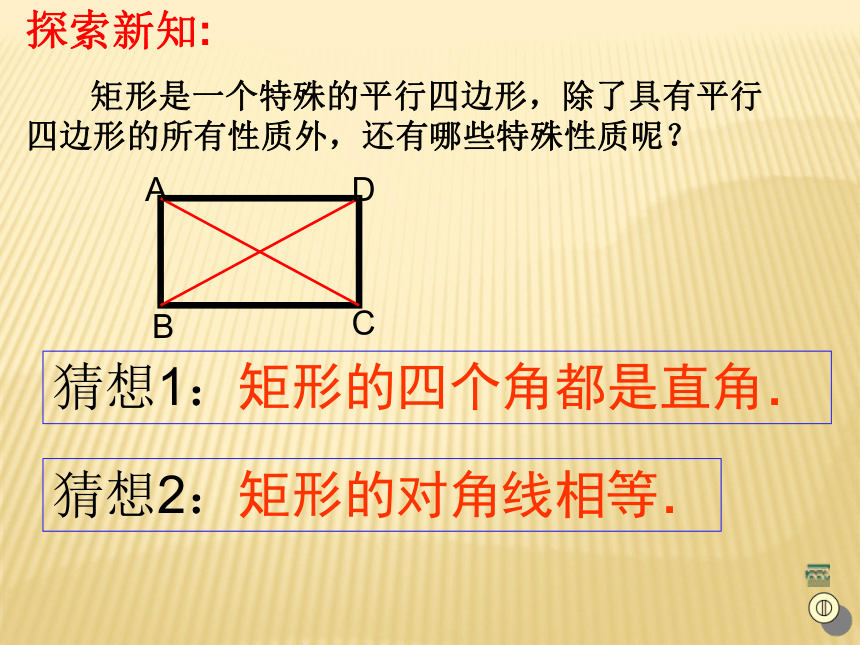
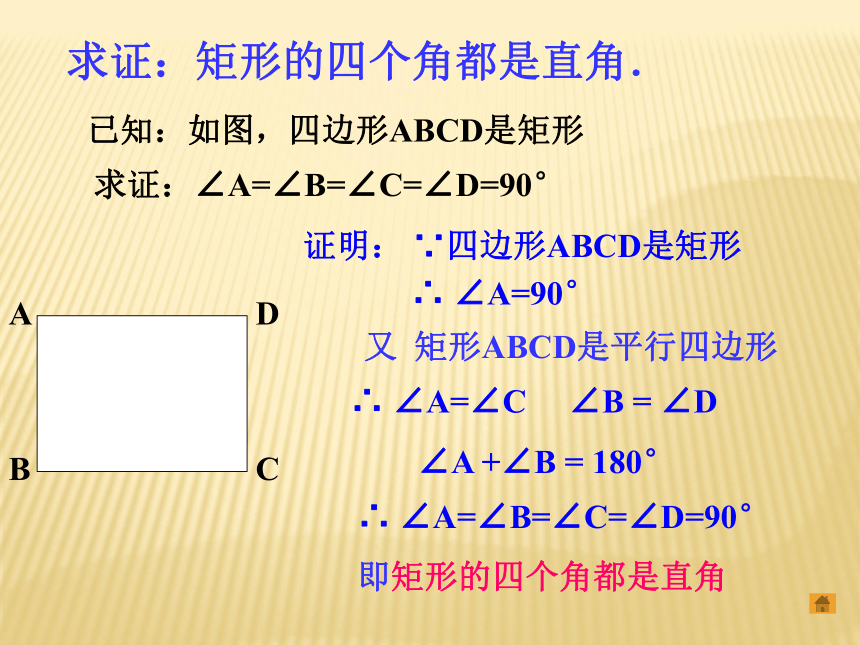
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
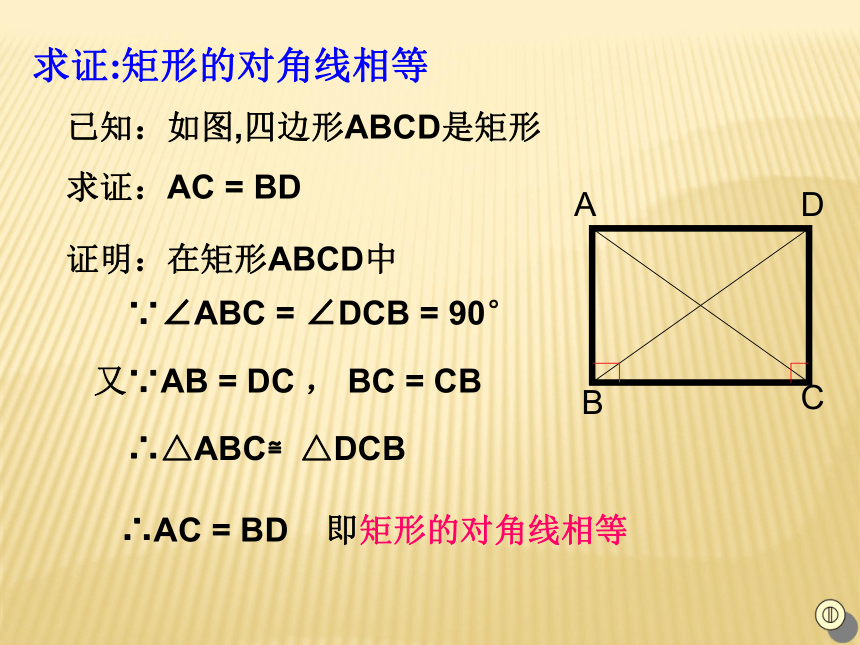
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
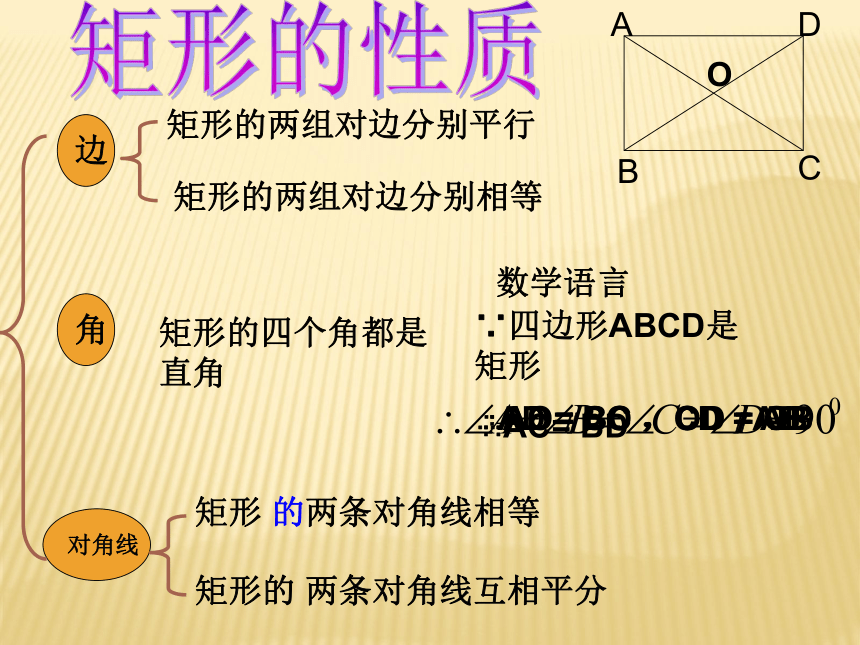
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的 两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD = BC ,CD = AB∴AD ∥BC ,CD ∥AB∴AC= BD ∴AO= CO ,OD = OB矩形的性质观察并思考下面这些物体是什么形状,它们是轴对称图形吗?是中心对称图形吗?有几条对称轴?比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形ABCDOOABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏 如图,在矩形ABCD中,找出相等的线段与相等的角。小试牛刀ODCBA相等的线段:AB=CD AD=BC AC=BD
OA=OC=OB=OD= AC= BD相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC
D证明: 延长BO至D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形. ∵∠ABC=900∴AC=BD再探新知推论:直角三角形斜边上的中线等于斜边的一半.例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形1.矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C练习1:2.四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
(2)若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
(3)若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
(4)若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°练一练3.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝, BD= 65 ㎝10本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半.18.2 特殊的平行四边形 18.2.1 矩形
第二课时 给我们一个四边形我们怎样才能判定它是一个矩形?判定定理1:(定义)
有一个角是直角的平行四边形是矩形。练习:如图,点M是平行四边形ABCD边
AB的中点,且MD=MC。
求证:四边形ABCD是矩形。对角线相等的平行四边形是矩形判定定理2: 同学们自己思考,证明看它是否成立练习:如图四边形ABCD为平行四边形,
两条对角线AC,BD相交于点O,并且AO=DO.
求证:ABCD是矩形。思考:小明同学用画“边——直角,边——直角,边——直角,边”这样四个步骤(如图)画出了一个四边形,她说这就是一个矩形。同学们相信吗?你能证明吗?判定定理3:有三个角是直角的四边形是矩形练习:如图,BD,BE分别是∠ABC与∠ABP的角平分线,AE⊥BE,AD⊥BD,E,D为垂足.
求证:四边形AEBD是矩形。推论:四个角都相等的四边形是矩形总结;判定一个四边形是矩形有几种方法?分别是什么?
F1.矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
2. 下面说法中正确的是 ( ).
A 有一个角是直角的四边形是矩形.
B 两条对角线相等的四边形是矩形.
C 两条对角线互相垂直的四边形是矩形.
D 四个角都是直角的四边形是矩形. 3.矩形的一组邻边长分别是3cm和4cm,则它的对角
线长是 cm. 一. 选择: 二. 填空: A D5课内练习4.已知:如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H。四边形EFGH是矩形吗 生活中的数学 给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理。学以致用本节课你有哪些收获?1. 矩形的定义:2. 矩形的性质:3. 矩形的判别:有一个内角是直角对角线相等 AC=BD,OA=OC,OB=OD.四边形ABCD
是矩形思想方法方面:1.有关矩形问题可化为直角三角形或等腰三角形的问题来解决.2.要判别一个四边形是矩形,一般要先判别它是平行四边形,然后再找直角或对角线相等”.
第一课时 两组对边分别平行的四边形是平行四边形平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新平行四边形的判定:两组对边分别平行的四边形;两组对边分别相等的四边形;两组对角分别相等的四边形;对角线互相平分的四边形;一组对边平行且相等的四边形;平行四边形的判定定理:一个角是
直角两组对边
分别平行矩形情景创设我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,也就是这堂课我们就来研究一种特殊的平行四边形—— 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等对角线互相平分矩形的一般性质:探索新知:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的 两条对角线互相平分矩形的两组对边分别相等矩形的两组对边分别平行矩形的四个角都是直角矩形 的两条对角线相等边对角线角数学语言∵四边形ABCD是矩形∴AD = BC ,CD = AB∴AD ∥BC ,CD ∥AB∴AC= BD ∴AO= CO ,OD = OB矩形的性质观察并思考下面这些物体是什么形状,它们是轴对称图形吗?是中心对称图形吗?有几条对称轴?比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形ABCDOOABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏 如图,在矩形ABCD中,找出相等的线段与相等的角。小试牛刀ODCBA相等的线段:AB=CD AD=BC AC=BD
OA=OC=OB=OD= AC= BD相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC
D证明: 延长BO至D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形. ∵∠ABC=900∴AC=BD再探新知推论:直角三角形斜边上的中线等于斜边的一半.例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形1.矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C练习1:2.四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
(2)若已知∠CAB=40°,则∠OCB=
∠OBA= ∠AOB= ∠AOD=
(3)若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
(4)若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝550°10100°40°12482880°练一练3.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝, BD= 65 ㎝10本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 推 论 直角三角形斜边上的中线等于斜边的一半.18.2 特殊的平行四边形 18.2.1 矩形
第二课时 给我们一个四边形我们怎样才能判定它是一个矩形?判定定理1:(定义)
有一个角是直角的平行四边形是矩形。练习:如图,点M是平行四边形ABCD边
AB的中点,且MD=MC。
求证:四边形ABCD是矩形。对角线相等的平行四边形是矩形判定定理2: 同学们自己思考,证明看它是否成立练习:如图四边形ABCD为平行四边形,
两条对角线AC,BD相交于点O,并且AO=DO.
求证:ABCD是矩形。思考:小明同学用画“边——直角,边——直角,边——直角,边”这样四个步骤(如图)画出了一个四边形,她说这就是一个矩形。同学们相信吗?你能证明吗?判定定理3:有三个角是直角的四边形是矩形练习:如图,BD,BE分别是∠ABC与∠ABP的角平分线,AE⊥BE,AD⊥BD,E,D为垂足.
求证:四边形AEBD是矩形。推论:四个角都相等的四边形是矩形总结;判定一个四边形是矩形有几种方法?分别是什么?
F1.矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
2. 下面说法中正确的是 ( ).
A 有一个角是直角的四边形是矩形.
B 两条对角线相等的四边形是矩形.
C 两条对角线互相垂直的四边形是矩形.
D 四个角都是直角的四边形是矩形. 3.矩形的一组邻边长分别是3cm和4cm,则它的对角
线长是 cm. 一. 选择: 二. 填空: A D5课内练习4.已知:如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H。四边形EFGH是矩形吗 生活中的数学 给你一根足够长的绳子,你能检查教室的门窗或你的桌子是不是矩形吗?你怎样检查?解释其中的道理。学以致用本节课你有哪些收获?1. 矩形的定义:2. 矩形的性质:3. 矩形的判别:有一个内角是直角对角线相等 AC=BD,OA=OC,OB=OD.四边形ABCD
是矩形思想方法方面:1.有关矩形问题可化为直角三角形或等腰三角形的问题来解决.2.要判别一个四边形是矩形,一般要先判别它是平行四边形,然后再找直角或对角线相等”.
