西安交通大学苏州附属初级中学 2023-2024学年上学期初二数学第十二周周练 (无答案)
文档属性
| 名称 | 西安交通大学苏州附属初级中学 2023-2024学年上学期初二数学第十二周周练 (无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 277.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 12:44:53 | ||
图片预览


文档简介
初二数学第十二周周练 卷一
一.选择题(共8小题,每题3分)
1.根据下列表述,能确定位置的是
A.东经,北纬 B.北京市二环路 C.东北 D.红星电影院2排
2.观察下列实数,,,,(相邻两个0之间的1的个数逐次增加,其中无理数的个数为
A.1 B.4 C.3 D.2
3.一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后的图形是
A. B. C. D.
4.若等腰三角形的顶角是,则它的一个底角的度数是
A. B. C.或 D.或
5.已知,那么化简代数式的结果是
A. B. C. D.3
6.设,,则,的大小关系是
A. B. C. D.
7.任何实数,可用表示不超过的最大整数,如,,现对72进行如下操作:,这样对72只需进行3次操作后变为1,类似的,对36只需进行 次操作后变为1.
A.1 B.2 C.3 D.4
8.已知三角形的三边长分别为、、,求其面积.
对此问题,中外数学家曾经进行过深入研究.
古希腊几何学家海伦,约公元50年),给出了求其面积的海伦公式:
,其中.①
我国南宋时期数学家秦九韶(约,给出了著名的秦九韶公式:
.②
若一个三角形的三边长依次为,,,请选用适当的公式求出这个三角形的面积为
A. B. C. D.
二.填空题(共8小题,每题3分)
9.比较大小: .
10.小明去市旅游,在从景点回酒店的路上迷路了,他连续问了3个人,得到下列3种回答:
甲:你住的酒店在这儿的东面;
乙:从这儿到你住的酒店大约要走两站路;
丙:你从这儿往东走,大约两站路的距离就是你住的酒店.
你认为 的回答能帮助小明准确找到所住的酒店.
11.小明从镜子中看到电子钟显示的时间是,那么实际时间为 .
第11题图 第13题图 第15题图
12.用四舍五入法把数2.345精确到十分位,所得的近似数是 .
13.如图,在中,,于点,,,则的长为 .
14.如果最简二次根式和是可以合并的二次根式,则 .
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点.若,,则 .
16.已知,,则的值 .
三.解答题(共8小题)
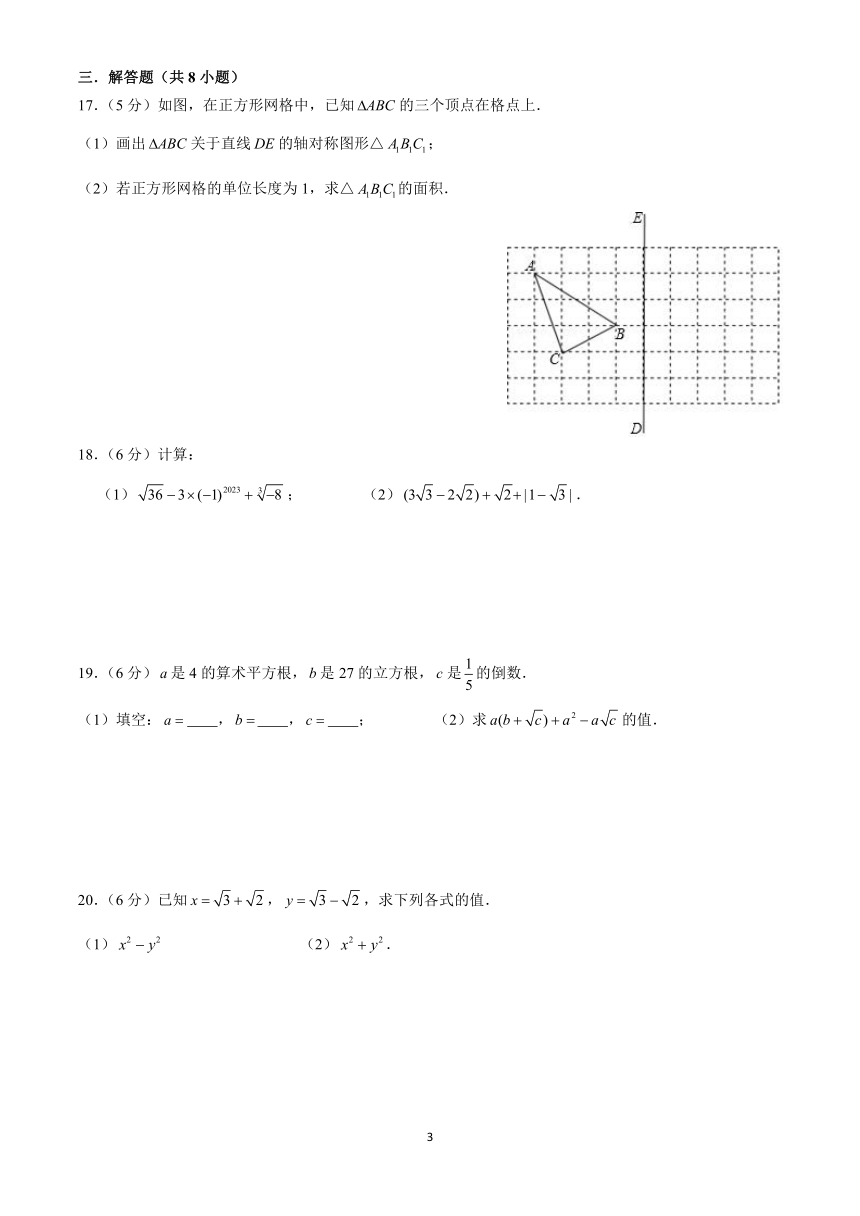
17.(5分)如图,在正方形网格中,已知的三个顶点在格点上.
(1)画出关于直线的轴对称图形△;
(2)若正方形网格的单位长度为1,求△的面积.
18.(6分)计算:
(1); (2).
19.(6分)是4的算术平方根,是27的立方根,是的倒数.
(1)填空: , , ; (2)求的值.
20.(6分)已知,,求下列各式的值.
(1) (2).
21.(6分)如图,在中,已知,是斜边的中点,交于点,连接.
(1)求证:;
(2)若,,求的周长.
22.(6分)观察下列计算,完成后面的问题:
验证:;
验证:;
验证:;
(1)按照上述三个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
(2)针对上述各式反映的规律,请用含的自然数)的等式表示出来.
23.(8分)阅读材料:
我们定义:如果一个数的平方等于,记作,那么这个就叫做虚数单位.虚数与我们学过的实数合在一起叫做复数.一个复数可以表示为,均为实数)的形式,其中叫做它的实部,叫做它的虚部.
复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似.
例如 计算:.
根据上述材料,解决下列问题:
(1)填空: , ;
(2)计算:;
(3)将化为,均为实数)的形式(即化为分母中不含的形式).
24.(9分)已知线段AB,CD相交于点O,且O为AB、CD的中点,AB=6cm,CD=16cm,∠AOC=60°点P在线段CD上由C向D运动,到点D后停止,速度为2cm/s,假设运动时间为t,在运动过程中,回答下列问题:
(1)连接AP,当△AOP为等腰三角形时,求出t的值;
(2)连接AP、BP,当△ABP为直角三角形时,求出t的值;
(3)当AP=6cm时,求出t的值;
(4)整个运动过程中,写出AP的取值范围:___________.
1
一.选择题(共8小题,每题3分)
1.根据下列表述,能确定位置的是
A.东经,北纬 B.北京市二环路 C.东北 D.红星电影院2排
2.观察下列实数,,,,(相邻两个0之间的1的个数逐次增加,其中无理数的个数为
A.1 B.4 C.3 D.2
3.一张正方形纸片经过两次对折,并在如图所示的位置上剪去一个小正方形,打开后的图形是
A. B. C. D.
4.若等腰三角形的顶角是,则它的一个底角的度数是
A. B. C.或 D.或
5.已知,那么化简代数式的结果是
A. B. C. D.3
6.设,,则,的大小关系是
A. B. C. D.
7.任何实数,可用表示不超过的最大整数,如,,现对72进行如下操作:,这样对72只需进行3次操作后变为1,类似的,对36只需进行 次操作后变为1.
A.1 B.2 C.3 D.4
8.已知三角形的三边长分别为、、,求其面积.
对此问题,中外数学家曾经进行过深入研究.
古希腊几何学家海伦,约公元50年),给出了求其面积的海伦公式:
,其中.①
我国南宋时期数学家秦九韶(约,给出了著名的秦九韶公式:
.②
若一个三角形的三边长依次为,,,请选用适当的公式求出这个三角形的面积为
A. B. C. D.
二.填空题(共8小题,每题3分)
9.比较大小: .
10.小明去市旅游,在从景点回酒店的路上迷路了,他连续问了3个人,得到下列3种回答:
甲:你住的酒店在这儿的东面;
乙:从这儿到你住的酒店大约要走两站路;
丙:你从这儿往东走,大约两站路的距离就是你住的酒店.
你认为 的回答能帮助小明准确找到所住的酒店.
11.小明从镜子中看到电子钟显示的时间是,那么实际时间为 .
第11题图 第13题图 第15题图
12.用四舍五入法把数2.345精确到十分位,所得的近似数是 .
13.如图,在中,,于点,,,则的长为 .
14.如果最简二次根式和是可以合并的二次根式,则 .
15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点.若,,则 .
16.已知,,则的值 .
三.解答题(共8小题)
17.(5分)如图,在正方形网格中,已知的三个顶点在格点上.
(1)画出关于直线的轴对称图形△;
(2)若正方形网格的单位长度为1,求△的面积.
18.(6分)计算:
(1); (2).
19.(6分)是4的算术平方根,是27的立方根,是的倒数.
(1)填空: , , ; (2)求的值.
20.(6分)已知,,求下列各式的值.
(1) (2).
21.(6分)如图,在中,已知,是斜边的中点,交于点,连接.
(1)求证:;
(2)若,,求的周长.
22.(6分)观察下列计算,完成后面的问题:
验证:;
验证:;
验证:;
(1)按照上述三个等式及其验证过程的基本思路,猜想的变形结果并进行验证;
(2)针对上述各式反映的规律,请用含的自然数)的等式表示出来.
23.(8分)阅读材料:
我们定义:如果一个数的平方等于,记作,那么这个就叫做虚数单位.虚数与我们学过的实数合在一起叫做复数.一个复数可以表示为,均为实数)的形式,其中叫做它的实部,叫做它的虚部.
复数的加、减、乘的运算与我们学过的整式加、减、乘的运算类似.
例如 计算:.
根据上述材料,解决下列问题:
(1)填空: , ;
(2)计算:;
(3)将化为,均为实数)的形式(即化为分母中不含的形式).
24.(9分)已知线段AB,CD相交于点O,且O为AB、CD的中点,AB=6cm,CD=16cm,∠AOC=60°点P在线段CD上由C向D运动,到点D后停止,速度为2cm/s,假设运动时间为t,在运动过程中,回答下列问题:
(1)连接AP,当△AOP为等腰三角形时,求出t的值;
(2)连接AP、BP,当△ABP为直角三角形时,求出t的值;
(3)当AP=6cm时,求出t的值;
(4)整个运动过程中,写出AP的取值范围:___________.
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
