第一章 三角形的证明单元测试卷(含答案)
文档属性
| 名称 | 第一章 三角形的证明单元测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024北师版数学八年级下学期
第一章 三角形的证明
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东清远期末)在△ABC中,∠B=∠C,AB=3,则AC的长为 ( )
A.2 B.3 C.4 D.5
2.下列命题的逆命题是假命题的是 ( )
A.同旁内角互补,两直线平行
B.全等三角形的对应边相等
C.全等三角形的对应角相等
D.线段垂直平分线上的点到线段两端的距离相等
3.(2022·广东广州黄埔区期末)如图,△ABC≌△AED,点D在BC边上.若∠EAB=50°,则∠ADE的度数是( )
A.50° B.60° C.65° D.30°
(第3题) (第4题)
4.(2021·山东济南槐荫区期末)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是点A(-3,0),B(-1,2),C(3,2),则到△ABC三个顶点距离相等的点的坐标是( )
A.(0,-1) B.(0,0)
C.(1,-1) D.(1,-2)
5.(2022·四川成都高新区段考)如图,Rt△ABC中,∠C=90°,∠CBA=60°.首先以顶点B为圆心、适当长为半径作弧,分别交边BC,BA于点E,D;然后分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若BG=8,P为边AB上一动点,连接GP,则GP的最小值为 ( )
A.2 B.4 C.8 D.无法确定
(第5题) (第6题)
6.(2022·四川成都青羊区期中)如图,在△ABC中,AB的垂直平分线DE分别与边AB,AC交于点D,E.已知△ABC与△BCE的周长分别为22 cm和14 cm,则BD的长为 ( )
A.3 cm B.5 cm C.6 cm D.4 cm
7.(2021·江苏苏州期末)定义:等腰三角形的一个底角与其顶角的度数的比值k(k>1)称为这个等腰三角形的“优美比”.若在等腰三角形ABC中,∠A=36°,则它的“优美比”k为 ( )
A. B.2 C. D.3
8.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO= ( )
A.2∶3∶4 B.1∶2∶3 C.1∶1∶1 D.3∶4∶5
(第8题) (第9题)
9. (2022·江苏泰州靖江实验学校期中)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E,F在斜边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD延长线上的点B'处,则线段B'F的长为 ( )
A. B. C.1 D.
10.如图,平面直角坐标系中存在点A(3,2),点B(1,0),以线段AB为边作等腰三角形ABP,且点P在坐标轴上,这样的点P有 ( )
A.4个 B.5个 C.6个 D.7个
二、填空题(共6小题,每小题3分,共18分)
11.如图,在Rt△ABC和Rt△EDF中,AB=DE,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.
(第11题) (第12题)
12.(2022·陕西渭南期末)如图,在Rt△ABC中,∠A=90°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且 MN平分∠AMC,若AN=2,则 NC的长为 .
13.(2022·陕西榆林期末)如图,点O在△ABC内,且到△ABC三边的距离相等,连接OB,OC,若∠BOC=120°,则∠A的度数是 .
(第13题) (第14题)
14.如图,在△ABC中,∠B=45°,∠C=30°,AB的垂直平分线分别交BC,AB于点D,E,AC的垂直平分线分别交BC,AC于点F,G,DF=1,则BC= .
15.(2022·河南洛阳期末)如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,则BC的长为 .
(第15题) (第16题)
16.(2021·湖南邵阳模拟)如图,在Rt△ACB中,∠ACB=90°,AB=13,AC=5,动点P从点B出发沿射线BC方向运动,当△APB为等腰三角形时,这个三角形的底边长可能为 .
三、解答题(共6小题,共52分)
17.(6分)(2022·江苏苏州期末)如图,△ABC中,EF垂直平分AC,交AC于点F,交BC于点E,连接AE且AE=AB.求证:∠B=2∠C.
18.(7分)(2021·广东佛山期中)如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.
(1)求证:AD垂直平分EF;
(2)若AB+AC=10,=15,∠EAF=60°,求AD的长.
19.(8分)(2022·江西赣州三中期中)如图,在等边三角形ABC的边AC,BC上分别取一点D,E,使AD=CE,AE,BD相交于点M.
(1)求证:AE=BD;
(2)若BE=2EC=4,求△ABC的面积.
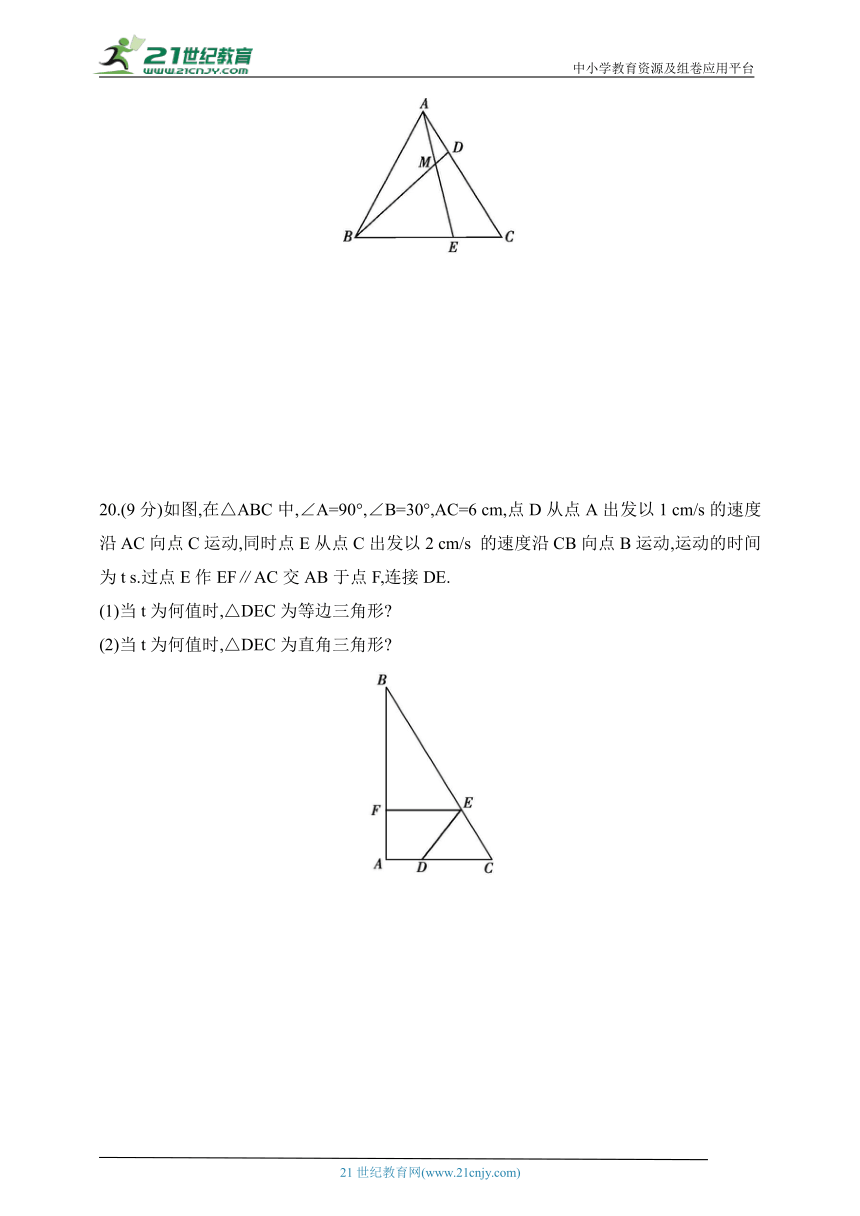
20.(9分)如图,在△ABC中,∠A=90°,∠B=30°,AC=6 cm,点D从点A出发以1 cm/s的速度沿AC向点C运动,同时点E从点C出发以2 cm/s 的速度沿CB向点B运动,运动的时间为t s.过点E作EF∥AC交AB于点F,连接DE.
(1)当t为何值时,△DEC为等边三角形
(2)当t为何值时,△DEC为直角三角形
21.(10分)(2022·广东广州黄埔区期末)如图,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,DE,AE分别为∠ADC,∠DAB的平分线.
(1)∠DEA= °;
(2)求证:CE=EB;
(3)探究CD,DA,AB三条线段之间的数量关系,并说明理由.
22.(12分)(1)如图(1),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①求证:△ADC≌△BEC;
②线段AD,BE之间的数量关系为 .
(2)如图(2),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE的高,连接BE.
①求∠AEB的度数;
②判断线段CM,AE,BE之间的数量关系,并证明.
(3)如图(3),△ABC是以BC为底的等腰直角三角形,点D是△ABC所在平面内一点,且满足AD=4,BD=6,CD=2,直接写出∠ADC的度数.
图(1) 图(2) 图(3)
第一章 三角形的证明
1 2 3 4 5 6 7 8 9 10
B C C D B D B A B D
11.BC=DF(答案不唯一) 12.4 13.60°
14.3+ 15.4 16.24,或13
1.B
如图,∵∠B=∠C,AB=3,∴AC=AB=3.
2.C A选项中的逆命题为“两直线平行,同旁内角互补”,是真命题;B选项中的逆命题为“对应边相等的两个三角形全等”,是真命题;C选项中的逆命题为“对应角相等的两个三角形全等”,是假命题;D选项中的逆命题为“到线段两端点距离相等的点在线段的垂直平分线上”,是真命题.故选C.
3.C ∵△ABC≌△AED,∴∠BAC=∠EAD,AD=AC,∠C=∠ADE,∴∠EAB+∠BAD =
∠DAC+∠BAD,∴∠DAC=∠EAB=50°.∵AD=AC,∴∠ADC=∠C=(180°-∠DAC)=65°,∴∠ADE=∠C=65°.故选C.
4.D
由题意可得,该点是线段BC与线段AB的垂直平分线的交点,如图,交点P的坐标为(1,-2).
5.B 由尺规作图步骤可得,BG平分ABC,∵∠C=90°,∠CBA=60°,∴∠CBG=∠ABG=
30°.∵BG=8,∴CG=BG=4.∵点G到AB的距离等于GC的长,GP长的最小值等于点G到AB的距离,∴GP长的最小值为4.
6.D ∵DE是AB的垂直平分线,∴EA=EB,AD=BD=AB.∵△BCE的周长是14 cm,
∴BC+BE+EC=14 cm,即AC+BC=14 cm.∵△ABC的周长是22 cm,∴AB+AC+BC=22 cm,
∴AB=22-14=8(cm),∴BD=AB=×8=4(cm).
7.B 当∠A为顶角时,一个底角为(180°-36°)=72°,此时,“优美比”k==2;当∠A为底角时,顶角为180°-36°-36°=108°,此时,“优美比”k==<1,不合题意,舍去.
8.A 根据角平分线的性质,可知点O到△ABC三边的距离相等,从而可得S△ABO∶
S△BCO∶S△CAO=AB∶BC∶CA=20∶30∶40=2∶3∶4.故选A.
9.B ∠ACB=90°,AC=3,BC=4,∴AB==5.由折叠得B'F=BF,∠AEC=∠DEC=
90°,∠ACE=∠DCE,∠B'CF=∠BCF,∴S△ABC=AB·CE=AC·BC,即×5CE=×3×4,解
得CE=,∴AE==.∵∠ACE=∠DCE,∠B'CF=∠BCF,∠ACB=90°,∴∠DCE+
∠B'CF=∠ACB=45°,即∠ECF=45°,∴△CEF是等腰直角三角形,∴EF=CE=,
∴BF=AB-AE-EF=,∴B'F=BF=.
10.D 由题意可知,以BP,BA为腰的等腰三角形有4个;以AP,BP为腰的等腰三角形有2个;以AP,AB为腰的等腰三角形有1个.所以这样的点P有7个.故选D.
本题的易错点是以AP,AB为腰的等腰三角形误以为有2个,其实只有1个,点P在x轴上,由A点的坐标与AB的长可以判断出点P与y轴没有交点.
11.BC=DF(AC=EF,AE=CF,∠B=∠D或∠BCA=∠F,答案不唯一) 添加BC=DF,在Rt△ABC和Rt△EDF中∴Rt△ABC≌Rt△EDF(HL).
12.4 ∵CM平分∠ACB,∴∠ACM=∠BCM.∵MN∥BC,∴∠CMN=∠BCM,∴∠CMN=∠ACM,
∴MN=CN,∴△MNC是等腰三角形.∵MN平分∠AMC,∴∠AMN=∠CMN,∴∠AMN=∠CMN=
∠ACM=∠BCM.∵∠A=90°,∴∠AMN=30°.∵AN=2,∴CN=MN=2AN=4.
13.60° ∵点O在△ABC内,且到△ABC三边的距离相等,∴OB平分∠ABC,OC平分∠ACB,∴∠ABC=2∠OBC,∠ACB=2∠OCB.∵∠OBC+∠OCB=180°-∠BOC=180°-120°=60°,∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2×60°=120°,∴∠A=180°-(∠ABC+∠ACB)=60°.
14.3+ 如图,过点D作DH⊥AF于点H,∴∠DHF=90°.∵∠B=45°,∠C=30°,DE,
FG分别为AB,AC的垂直平分线,∴AD=BD,AF=CF,∴∠BAD=∠B=45°,∠FAC=∠C=
30°,∴∠AFD=60°,∴∠HDF=30°.∵DF=1,∴FH=,DH=.易得AD=,AH=,∴AD=
BD=,FC=AF=AH+HF=2,∴BC=3+.
∵DE,FG分别为AB,AC的垂直平分线,∴AD=BD,AF=CF,∴∠DAB=∠B=45°,∠FAC=∠C=30°,∴∠ADF=90°,∠AFD=60°,∴∠DAF=30°,∴AF=2DF=2,AD=,∴BC=BD+DF+FC=AD+DF+AF=3+.
15.4 如图, 延长AD到点E,使DE=AD,连接CE.在△ADB和△EDC中,
∴△ABD≌△ECD(SAS),∴EC=AB=6,DE=DA=4.∵AE=2AD=8,AC=10,
∴AE2+EC2=AC2,∴△AEC是直角三角形,∴CD==2,∴CB=2CD=4.
遇到“中点”或“中线”,常考虑倍长中线模型,构造两个三角形全等.
图(1)
图(2)
16.24,或13 (分类讨论思想)由勾股定理可得BC===12,分以下三种情况讨论:①如图(1),当点A为等腰三角形APB的顶点时,AB=AP,此时BP=
2BC=2×12=24;②如图(2),当点B为等腰三角形APB的顶点时,BA=BP=13,此时,在Rt△ACP中,由勾股定理得AP===;③如图(3),当点P为等腰三角形APB的顶点时,PA=PB,此时,底边AB=13.综上所述,当△ABP为等腰三角形时,这个三角形的底边长可能为24,或13.
17.【参考答案】证明:∵AE=AB,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,∠B=∠AEB,
∴∠B=∠AEB=∠C+∠CAE=2∠C. (6分)
18.【参考答案】(1)证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF. (2分)
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),∴AE=AF. (3分)
∵DE=DF,∴AD垂直平分EF. (4分)
(2)∵DE=DF,
∴S△ABC=S△ABD+S△ACD=AB·DE+AC·DF=DE·(AB+AC)=15. (6分)
∵AB+AC=10,
∴×10×DE=15,∴DE=3.
∵∠EAF=60°,∴∠DAF=∠EAD=30°,
∴AD=2DE=6. (7分)
19.
(1)→△ACE≌△BAD→AE=BD
【参考答案】(1)证明:∵△ABC为等边三角形,
∴AB=CA,∠BAD=∠ACE=60°.
在△BAD和△ACE中,
∴△ACE≌△BAD,∴AE=BD. (4分)
(2)如图,作AF⊥BC于点F,
由“三线合一”知,∠BAF=30°.
∵BE=2EC=4,∴BC=BE+EC=4+2=6,
∴AB=6,BF=3.
由勾股定理得AF==3,
∴S△ABC=BC·AF=×6×3=9. (8分)
20.【参考答案】由题意得CD=6-t,CE=2t.
(1)若△DEC为等边三角形,则EC=DC,
即2t=6-t,
解得t=2.
故当t为2时,△DEC为等边三角形. (2分)
(2)当∠CED=90°时,CD=2EC,即6-t=2×2t,
解得t=1.2; (5分)
当∠CDE=90°时,CE=2CD,即2t=2(6-t),
解得t=3. (7分)
故当t为1.2或3时,△DEC为直角三角形. (9分)
21.
(1)∠B=∠C=90°→AB∥CD→∠ADC+∠DAB=180°
→∠EDA+∠DAE=90°→∠DEA
(2)作EF⊥AD于点F→CE=EB
(3)→CD+AB=AD
【参考答案】(1)90° (2分)
解法提示:∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,
∴∠ADC+∠DAB=180°.
∵DE,AE分别为∠ADC,∠DAB的平分线,
∴∠EDA=∠ADC,∠DAE=∠DAB,
∴∠EDA+∠DAE=(∠ADC + ∠DAB )=×180°=90°,
∴∠DEA=180°-(∠EDA+∠DAE)=90°.
(2)证明:如图,作EF⊥AD于点F,
∵DE平分∠ADC,且∠C=90°,EF⊥AD,
∴CE=FE.
∵AE平分∠DAB,且∠B=90°,EF⊥AD,
∴EF=EB,∴CE=EB. (5分)
(3)如图,在Rt△DCE和Rt△DFE中,
∴Rt△DCE≌Rt△DFE,∴DC=DF.
同理可证Rt△AFE≌Rt△ABE,∴AF=AB,
∴CD+AB=DF+AF=AD. (10分)
本题第(3)问,除上述方法外,还有以下两种解题方法:
方法一 如图,延长DE交AB的延长线于点F,
由(1)知∠DEA=90°,
∴∠DEA=∠FEA=90°.
∵AE平分∠DAB,∴∠DAE=∠FAE.
∵AE=AE,∴△DAE≌△FAE,
∴AD=AF,DE=EF.
∵∠ABC=∠C=90°,∠DEC=∠FEB,
∴△DCE≌△FBE,∴CD=BF,
∴AD=AF=BF+AB=CD+AB. (10分)
方法二 如图,延长DE交AB的延长线于点F,
∵∠ABC=∠C=90°,∴CD∥AB, ∴∠CDE=∠AFD.
∵DE为∠ADC的平分线,∴∠CDE=∠ADE,
∴∠ADE=∠AFD,∴AD=AF.
由(1)知∠DEA=90°,∴DE=FE.
∵∠CDE=∠AFD,∠CED=∠BEF,
∴△DCE≌△FBE,∴CD=BF,
∴AD=AF=BF+AB=CD+AB. (10分)
22.【参考答案】(1)①证明:∵△ACB和△DCE均为等边三角形,
∴AC=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠ECB,
∴△ADC≌△BEC(SAS). (2分)
②AD=BE (4分)
(2)①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=CB,CD=CE.
又∠ACB=∠DCE=90°,
∴∠ACD+∠DCB=∠ECB+∠DCB=90°,
∴∠ACD=∠ECB.
在△ACD和△BCE中,
∴△ACD≌△BCE,
∴∠ADC=∠BEC.
∵点A,D,E在同一直线上,
∴∠BEC=∠ADC=180°-∠CDE=180°-45°=135°,
∴∠AEB=135°-∠CED=135°-45°=90°. (7分)
②AE=BE+2CM. (8分)
证明:∵△CDA≌△CEB,
∴AD=BE.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DE=2CM,
∴AE=AD+DE=BE+2CM. (9分)
(3)135°或45°. (12分)
解法提示:当点D在△ABC内时,如图(1),过点A作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△CAE≌△BAD(SAS),
∴CE=BD=6.
∵DE=AD=4,CD=2,
∴EC2=ED2+CD2,
∴∠EDC=90°.
∵∠ADE=45°,
∴∠ADC=45°+90°=135°.
②当点D在△ABC外时,如图(2),过点A作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴CE=BD=6.
∵DE=AD=4,CD=2,
∴EC2=ED2+CD2,
∴∠EDC=90°.
∵∠ADE=45°,
∴∠ADC=45°.
综上所述,∠ADC的度数为135°或45°.
图(1) 图(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版数学八年级下学期
第一章 三角形的证明
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东清远期末)在△ABC中,∠B=∠C,AB=3,则AC的长为 ( )
A.2 B.3 C.4 D.5
2.下列命题的逆命题是假命题的是 ( )
A.同旁内角互补,两直线平行
B.全等三角形的对应边相等
C.全等三角形的对应角相等
D.线段垂直平分线上的点到线段两端的距离相等
3.(2022·广东广州黄埔区期末)如图,△ABC≌△AED,点D在BC边上.若∠EAB=50°,则∠ADE的度数是( )
A.50° B.60° C.65° D.30°
(第3题) (第4题)
4.(2021·山东济南槐荫区期末)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是点A(-3,0),B(-1,2),C(3,2),则到△ABC三个顶点距离相等的点的坐标是( )
A.(0,-1) B.(0,0)
C.(1,-1) D.(1,-2)
5.(2022·四川成都高新区段考)如图,Rt△ABC中,∠C=90°,∠CBA=60°.首先以顶点B为圆心、适当长为半径作弧,分别交边BC,BA于点E,D;然后分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若BG=8,P为边AB上一动点,连接GP,则GP的最小值为 ( )
A.2 B.4 C.8 D.无法确定
(第5题) (第6题)
6.(2022·四川成都青羊区期中)如图,在△ABC中,AB的垂直平分线DE分别与边AB,AC交于点D,E.已知△ABC与△BCE的周长分别为22 cm和14 cm,则BD的长为 ( )
A.3 cm B.5 cm C.6 cm D.4 cm
7.(2021·江苏苏州期末)定义:等腰三角形的一个底角与其顶角的度数的比值k(k>1)称为这个等腰三角形的“优美比”.若在等腰三角形ABC中,∠A=36°,则它的“优美比”k为 ( )
A. B.2 C. D.3
8.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO= ( )
A.2∶3∶4 B.1∶2∶3 C.1∶1∶1 D.3∶4∶5
(第8题) (第9题)
9. (2022·江苏泰州靖江实验学校期中)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E,F在斜边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD延长线上的点B'处,则线段B'F的长为 ( )
A. B. C.1 D.
10.如图,平面直角坐标系中存在点A(3,2),点B(1,0),以线段AB为边作等腰三角形ABP,且点P在坐标轴上,这样的点P有 ( )
A.4个 B.5个 C.6个 D.7个
二、填空题(共6小题,每小题3分,共18分)
11.如图,在Rt△ABC和Rt△EDF中,AB=DE,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.
(第11题) (第12题)
12.(2022·陕西渭南期末)如图,在Rt△ABC中,∠A=90°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且 MN平分∠AMC,若AN=2,则 NC的长为 .
13.(2022·陕西榆林期末)如图,点O在△ABC内,且到△ABC三边的距离相等,连接OB,OC,若∠BOC=120°,则∠A的度数是 .
(第13题) (第14题)
14.如图,在△ABC中,∠B=45°,∠C=30°,AB的垂直平分线分别交BC,AB于点D,E,AC的垂直平分线分别交BC,AC于点F,G,DF=1,则BC= .
15.(2022·河南洛阳期末)如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,则BC的长为 .
(第15题) (第16题)
16.(2021·湖南邵阳模拟)如图,在Rt△ACB中,∠ACB=90°,AB=13,AC=5,动点P从点B出发沿射线BC方向运动,当△APB为等腰三角形时,这个三角形的底边长可能为 .
三、解答题(共6小题,共52分)
17.(6分)(2022·江苏苏州期末)如图,△ABC中,EF垂直平分AC,交AC于点F,交BC于点E,连接AE且AE=AB.求证:∠B=2∠C.
18.(7分)(2021·广东佛山期中)如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.
(1)求证:AD垂直平分EF;
(2)若AB+AC=10,=15,∠EAF=60°,求AD的长.
19.(8分)(2022·江西赣州三中期中)如图,在等边三角形ABC的边AC,BC上分别取一点D,E,使AD=CE,AE,BD相交于点M.
(1)求证:AE=BD;
(2)若BE=2EC=4,求△ABC的面积.
20.(9分)如图,在△ABC中,∠A=90°,∠B=30°,AC=6 cm,点D从点A出发以1 cm/s的速度沿AC向点C运动,同时点E从点C出发以2 cm/s 的速度沿CB向点B运动,运动的时间为t s.过点E作EF∥AC交AB于点F,连接DE.
(1)当t为何值时,△DEC为等边三角形
(2)当t为何值时,△DEC为直角三角形
21.(10分)(2022·广东广州黄埔区期末)如图,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,DE,AE分别为∠ADC,∠DAB的平分线.
(1)∠DEA= °;
(2)求证:CE=EB;
(3)探究CD,DA,AB三条线段之间的数量关系,并说明理由.
22.(12分)(1)如图(1),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①求证:△ADC≌△BEC;
②线段AD,BE之间的数量关系为 .
(2)如图(2),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE的高,连接BE.
①求∠AEB的度数;
②判断线段CM,AE,BE之间的数量关系,并证明.
(3)如图(3),△ABC是以BC为底的等腰直角三角形,点D是△ABC所在平面内一点,且满足AD=4,BD=6,CD=2,直接写出∠ADC的度数.
图(1) 图(2) 图(3)
第一章 三角形的证明
1 2 3 4 5 6 7 8 9 10
B C C D B D B A B D
11.BC=DF(答案不唯一) 12.4 13.60°
14.3+ 15.4 16.24,或13
1.B
如图,∵∠B=∠C,AB=3,∴AC=AB=3.
2.C A选项中的逆命题为“两直线平行,同旁内角互补”,是真命题;B选项中的逆命题为“对应边相等的两个三角形全等”,是真命题;C选项中的逆命题为“对应角相等的两个三角形全等”,是假命题;D选项中的逆命题为“到线段两端点距离相等的点在线段的垂直平分线上”,是真命题.故选C.
3.C ∵△ABC≌△AED,∴∠BAC=∠EAD,AD=AC,∠C=∠ADE,∴∠EAB+∠BAD =
∠DAC+∠BAD,∴∠DAC=∠EAB=50°.∵AD=AC,∴∠ADC=∠C=(180°-∠DAC)=65°,∴∠ADE=∠C=65°.故选C.
4.D
由题意可得,该点是线段BC与线段AB的垂直平分线的交点,如图,交点P的坐标为(1,-2).
5.B 由尺规作图步骤可得,BG平分ABC,∵∠C=90°,∠CBA=60°,∴∠CBG=∠ABG=
30°.∵BG=8,∴CG=BG=4.∵点G到AB的距离等于GC的长,GP长的最小值等于点G到AB的距离,∴GP长的最小值为4.
6.D ∵DE是AB的垂直平分线,∴EA=EB,AD=BD=AB.∵△BCE的周长是14 cm,
∴BC+BE+EC=14 cm,即AC+BC=14 cm.∵△ABC的周长是22 cm,∴AB+AC+BC=22 cm,
∴AB=22-14=8(cm),∴BD=AB=×8=4(cm).
7.B 当∠A为顶角时,一个底角为(180°-36°)=72°,此时,“优美比”k==2;当∠A为底角时,顶角为180°-36°-36°=108°,此时,“优美比”k==<1,不合题意,舍去.
8.A 根据角平分线的性质,可知点O到△ABC三边的距离相等,从而可得S△ABO∶
S△BCO∶S△CAO=AB∶BC∶CA=20∶30∶40=2∶3∶4.故选A.
9.B ∠ACB=90°,AC=3,BC=4,∴AB==5.由折叠得B'F=BF,∠AEC=∠DEC=
90°,∠ACE=∠DCE,∠B'CF=∠BCF,∴S△ABC=AB·CE=AC·BC,即×5CE=×3×4,解
得CE=,∴AE==.∵∠ACE=∠DCE,∠B'CF=∠BCF,∠ACB=90°,∴∠DCE+
∠B'CF=∠ACB=45°,即∠ECF=45°,∴△CEF是等腰直角三角形,∴EF=CE=,
∴BF=AB-AE-EF=,∴B'F=BF=.
10.D 由题意可知,以BP,BA为腰的等腰三角形有4个;以AP,BP为腰的等腰三角形有2个;以AP,AB为腰的等腰三角形有1个.所以这样的点P有7个.故选D.
本题的易错点是以AP,AB为腰的等腰三角形误以为有2个,其实只有1个,点P在x轴上,由A点的坐标与AB的长可以判断出点P与y轴没有交点.
11.BC=DF(AC=EF,AE=CF,∠B=∠D或∠BCA=∠F,答案不唯一) 添加BC=DF,在Rt△ABC和Rt△EDF中∴Rt△ABC≌Rt△EDF(HL).
12.4 ∵CM平分∠ACB,∴∠ACM=∠BCM.∵MN∥BC,∴∠CMN=∠BCM,∴∠CMN=∠ACM,
∴MN=CN,∴△MNC是等腰三角形.∵MN平分∠AMC,∴∠AMN=∠CMN,∴∠AMN=∠CMN=
∠ACM=∠BCM.∵∠A=90°,∴∠AMN=30°.∵AN=2,∴CN=MN=2AN=4.
13.60° ∵点O在△ABC内,且到△ABC三边的距离相等,∴OB平分∠ABC,OC平分∠ACB,∴∠ABC=2∠OBC,∠ACB=2∠OCB.∵∠OBC+∠OCB=180°-∠BOC=180°-120°=60°,∴∠ABC+∠ACB=2(∠OBC+∠OCB)=2×60°=120°,∴∠A=180°-(∠ABC+∠ACB)=60°.
14.3+ 如图,过点D作DH⊥AF于点H,∴∠DHF=90°.∵∠B=45°,∠C=30°,DE,
FG分别为AB,AC的垂直平分线,∴AD=BD,AF=CF,∴∠BAD=∠B=45°,∠FAC=∠C=
30°,∴∠AFD=60°,∴∠HDF=30°.∵DF=1,∴FH=,DH=.易得AD=,AH=,∴AD=
BD=,FC=AF=AH+HF=2,∴BC=3+.
∵DE,FG分别为AB,AC的垂直平分线,∴AD=BD,AF=CF,∴∠DAB=∠B=45°,∠FAC=∠C=30°,∴∠ADF=90°,∠AFD=60°,∴∠DAF=30°,∴AF=2DF=2,AD=,∴BC=BD+DF+FC=AD+DF+AF=3+.
15.4 如图, 延长AD到点E,使DE=AD,连接CE.在△ADB和△EDC中,
∴△ABD≌△ECD(SAS),∴EC=AB=6,DE=DA=4.∵AE=2AD=8,AC=10,
∴AE2+EC2=AC2,∴△AEC是直角三角形,∴CD==2,∴CB=2CD=4.
遇到“中点”或“中线”,常考虑倍长中线模型,构造两个三角形全等.
图(1)
图(2)
16.24,或13 (分类讨论思想)由勾股定理可得BC===12,分以下三种情况讨论:①如图(1),当点A为等腰三角形APB的顶点时,AB=AP,此时BP=
2BC=2×12=24;②如图(2),当点B为等腰三角形APB的顶点时,BA=BP=13,此时,在Rt△ACP中,由勾股定理得AP===;③如图(3),当点P为等腰三角形APB的顶点时,PA=PB,此时,底边AB=13.综上所述,当△ABP为等腰三角形时,这个三角形的底边长可能为24,或13.
17.【参考答案】证明:∵AE=AB,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,∠B=∠AEB,
∴∠B=∠AEB=∠C+∠CAE=2∠C. (6分)
18.【参考答案】(1)证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF. (2分)
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),∴AE=AF. (3分)
∵DE=DF,∴AD垂直平分EF. (4分)
(2)∵DE=DF,
∴S△ABC=S△ABD+S△ACD=AB·DE+AC·DF=DE·(AB+AC)=15. (6分)
∵AB+AC=10,
∴×10×DE=15,∴DE=3.
∵∠EAF=60°,∴∠DAF=∠EAD=30°,
∴AD=2DE=6. (7分)
19.
(1)→△ACE≌△BAD→AE=BD
【参考答案】(1)证明:∵△ABC为等边三角形,
∴AB=CA,∠BAD=∠ACE=60°.
在△BAD和△ACE中,
∴△ACE≌△BAD,∴AE=BD. (4分)
(2)如图,作AF⊥BC于点F,
由“三线合一”知,∠BAF=30°.
∵BE=2EC=4,∴BC=BE+EC=4+2=6,
∴AB=6,BF=3.
由勾股定理得AF==3,
∴S△ABC=BC·AF=×6×3=9. (8分)
20.【参考答案】由题意得CD=6-t,CE=2t.
(1)若△DEC为等边三角形,则EC=DC,
即2t=6-t,
解得t=2.
故当t为2时,△DEC为等边三角形. (2分)
(2)当∠CED=90°时,CD=2EC,即6-t=2×2t,
解得t=1.2; (5分)
当∠CDE=90°时,CE=2CD,即2t=2(6-t),
解得t=3. (7分)
故当t为1.2或3时,△DEC为直角三角形. (9分)
21.
(1)∠B=∠C=90°→AB∥CD→∠ADC+∠DAB=180°
→∠EDA+∠DAE=90°→∠DEA
(2)作EF⊥AD于点F→CE=EB
(3)→CD+AB=AD
【参考答案】(1)90° (2分)
解法提示:∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,
∴∠ADC+∠DAB=180°.
∵DE,AE分别为∠ADC,∠DAB的平分线,
∴∠EDA=∠ADC,∠DAE=∠DAB,
∴∠EDA+∠DAE=(∠ADC + ∠DAB )=×180°=90°,
∴∠DEA=180°-(∠EDA+∠DAE)=90°.
(2)证明:如图,作EF⊥AD于点F,
∵DE平分∠ADC,且∠C=90°,EF⊥AD,
∴CE=FE.
∵AE平分∠DAB,且∠B=90°,EF⊥AD,
∴EF=EB,∴CE=EB. (5分)
(3)如图,在Rt△DCE和Rt△DFE中,
∴Rt△DCE≌Rt△DFE,∴DC=DF.
同理可证Rt△AFE≌Rt△ABE,∴AF=AB,
∴CD+AB=DF+AF=AD. (10分)
本题第(3)问,除上述方法外,还有以下两种解题方法:
方法一 如图,延长DE交AB的延长线于点F,
由(1)知∠DEA=90°,
∴∠DEA=∠FEA=90°.
∵AE平分∠DAB,∴∠DAE=∠FAE.
∵AE=AE,∴△DAE≌△FAE,
∴AD=AF,DE=EF.
∵∠ABC=∠C=90°,∠DEC=∠FEB,
∴△DCE≌△FBE,∴CD=BF,
∴AD=AF=BF+AB=CD+AB. (10分)
方法二 如图,延长DE交AB的延长线于点F,
∵∠ABC=∠C=90°,∴CD∥AB, ∴∠CDE=∠AFD.
∵DE为∠ADC的平分线,∴∠CDE=∠ADE,
∴∠ADE=∠AFD,∴AD=AF.
由(1)知∠DEA=90°,∴DE=FE.
∵∠CDE=∠AFD,∠CED=∠BEF,
∴△DCE≌△FBE,∴CD=BF,
∴AD=AF=BF+AB=CD+AB. (10分)
22.【参考答案】(1)①证明:∵△ACB和△DCE均为等边三角形,
∴AC=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠ECB+∠DCB=60°,
∴∠ACD=∠ECB,
∴△ADC≌△BEC(SAS). (2分)
②AD=BE (4分)
(2)①∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=CB,CD=CE.
又∠ACB=∠DCE=90°,
∴∠ACD+∠DCB=∠ECB+∠DCB=90°,
∴∠ACD=∠ECB.
在△ACD和△BCE中,
∴△ACD≌△BCE,
∴∠ADC=∠BEC.
∵点A,D,E在同一直线上,
∴∠BEC=∠ADC=180°-∠CDE=180°-45°=135°,
∴∠AEB=135°-∠CED=135°-45°=90°. (7分)
②AE=BE+2CM. (8分)
证明:∵△CDA≌△CEB,
∴AD=BE.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DE=2CM,
∴AE=AD+DE=BE+2CM. (9分)
(3)135°或45°. (12分)
解法提示:当点D在△ABC内时,如图(1),过点A作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△CAE≌△BAD(SAS),
∴CE=BD=6.
∵DE=AD=4,CD=2,
∴EC2=ED2+CD2,
∴∠EDC=90°.
∵∠ADE=45°,
∴∠ADC=45°+90°=135°.
②当点D在△ABC外时,如图(2),过点A作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴CE=BD=6.
∵DE=AD=4,CD=2,
∴EC2=ED2+CD2,
∴∠EDC=90°.
∵∠ADE=45°,
∴∠ADC=45°.
综上所述,∠ADC的度数为135°或45°.
图(1) 图(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
