第六章 平行四边形单元测试卷(含答案)
文档属性
| 名称 | 第六章 平行四边形单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 17:17:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师版数学八年级下学期
第六章 平行四边形
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东中考)如图,在△ABC中,BC=4,点D,E分别为AB,AC的中点,则DE= ( )
A. B.
C.1 D.2
(第1题) (第2题)
2.(2022·福建南平期末)如图,在平行四边形ABCD中,若∠A+∠C=120°,则∠D的度数为( )
A.120° B.60°
C.30° D.150°
3.(2022·四川凉山期末)如图,在平行四边形ABCD中,AC,BD相交于点O,AC=8,BD=10,则AD的长的取值范围是 ( )
A.AD>1 B.AD<9
C.19
(第3题) (第4题)
4.(2021·山西模拟改编)如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判定四边形ABCD是平行四边形的是 ( )
A.AB=CD B.AD∥BC
C.OA=OC D.AD=BC
5.[贴近校园生活](2022·山东济南期末)足球表面为什么由正六边形和正五边形构成 因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角,而又不足一个周角.这样,由平面折叠而成的多面体充气后最终就呈现为球形.如图,在折叠前的平面上,拼接点处的缝隙∠AOB的大小为 ( )
A.10° B.12° C.14° D.16°
6.(2021·重庆期末)如图,△AOB与△AOD的周长之差为5,且AB=2AD,则 ABCD的周长是( )
A.15 B.20 C.30 D.40
(第6题) (第7题)
7.(2022·四川乐山中考)如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为 ( )
A.4 B.3 C. D.2
8.(2021·河北中考)如图(1), ABCD中,AD>AB,∠ABC为锐角,要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图(2)中的甲、乙、丙三种方案,则正确的方案( )
取BD中点O,作BN=NO,OM=MD
作CM⊥BD于M,AN⊥BD于N
作AN,CM分别平分∠BAD,∠BCD
图(1) 图(2)
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
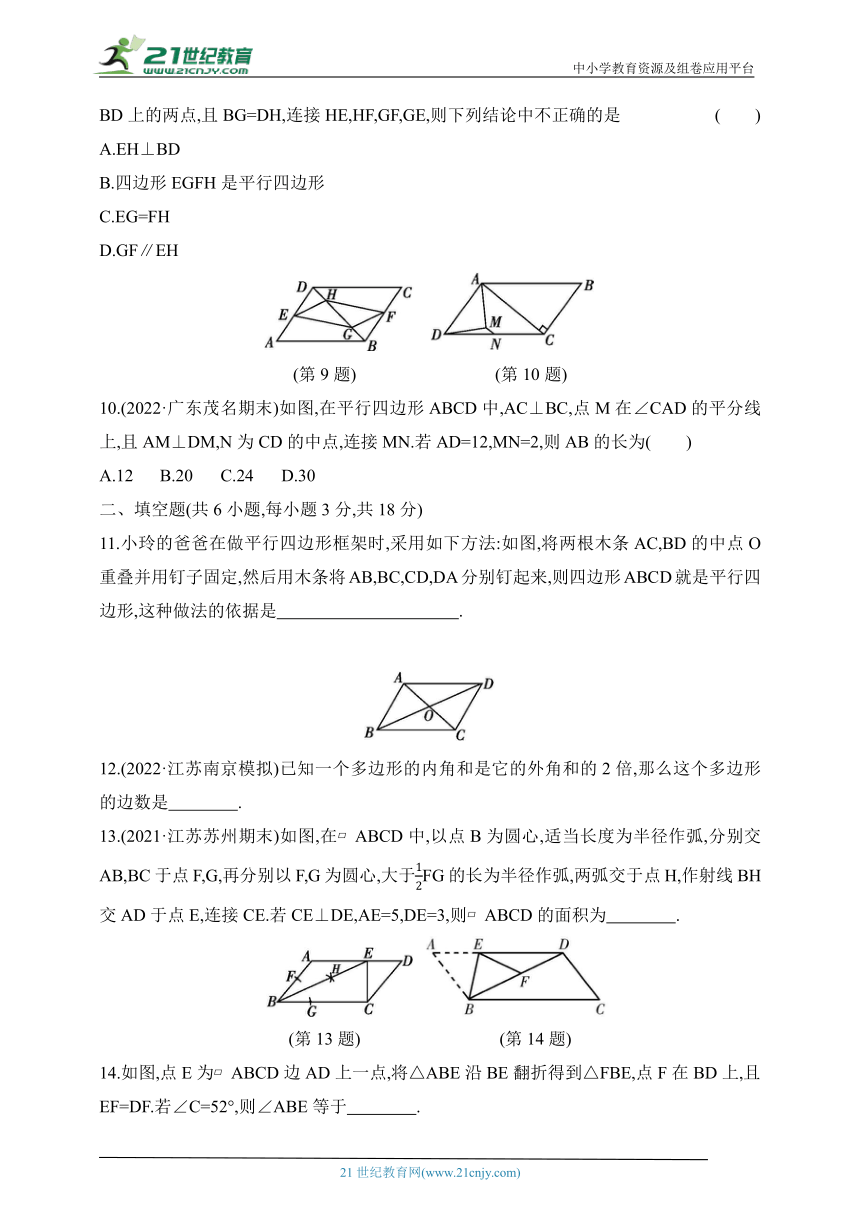
9.(2022·河北保定期末)如图,点E,F分别是 ABCD的边AD,BC的中点,点G,H是对角线BD上的两点,且BG=DH,连接HE,HF,GF,GE,则下列结论中不正确的是 ( )
A.EH⊥BD
B.四边形EGFH是平行四边形
C.EG=FH
D.GF∥EH
(第9题) (第10题)
10.(2022·广东茂名期末)如图,在平行四边形ABCD中,AC⊥BC,点M在∠CAD的平分线上,且AM⊥DM,N为CD的中点,连接MN.若AD=12,MN=2,则AB的长为( )
A.12 B.20 C.24 D.30
二、填空题(共6小题,每小题3分,共18分)
11.小玲的爸爸在做平行四边形框架时,采用如下方法:如图,将两根木条AC,BD的中点O重叠并用钉子固定,然后用木条将AB,BC,CD,DA分别钉起来,则四边形ABCD就是平行四边形,这种做法的依据是 .
12.(2022·江苏南京模拟)已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是 .
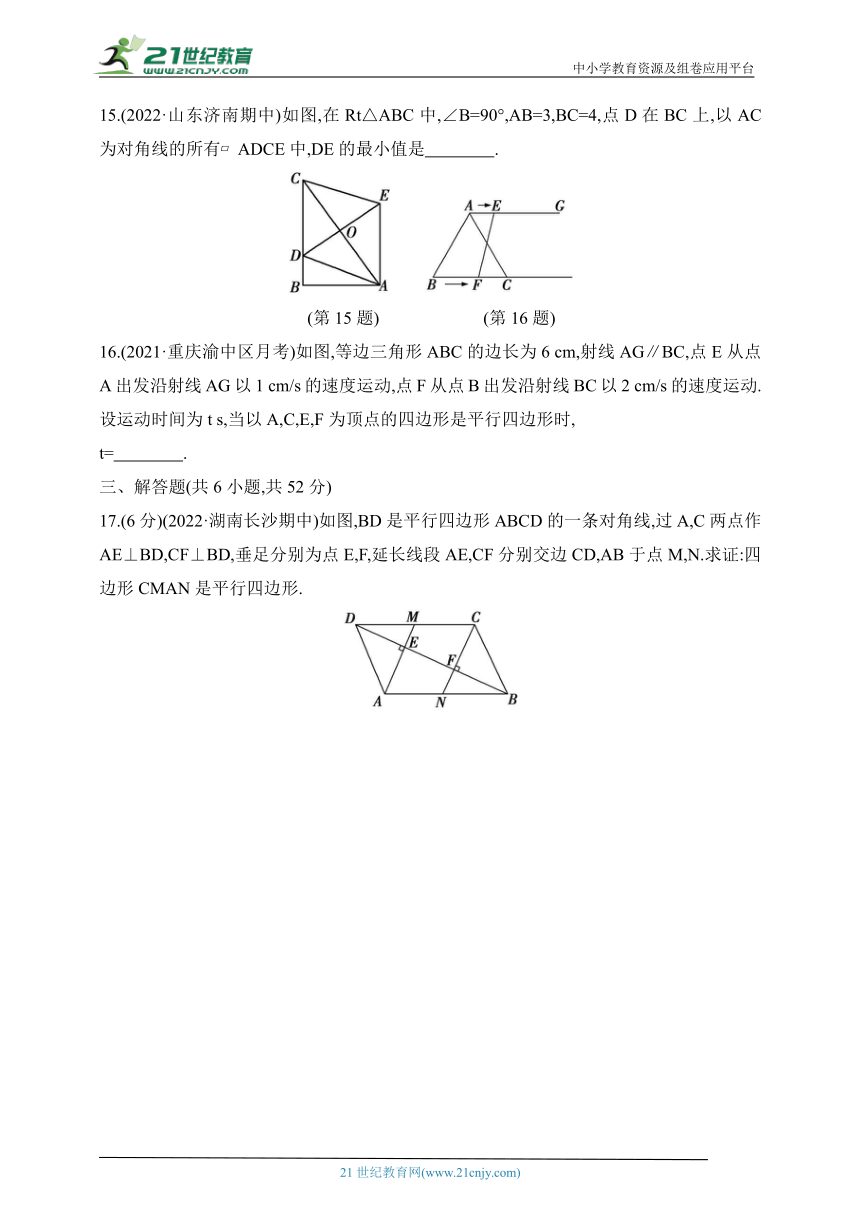
13.(2021·江苏苏州期末)如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以F,G为圆心,大于FG的长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥DE,AE=5,DE=3,则 ABCD的面积为 .
(第13题) (第14题)
14.如图,点E为 ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE等于 .
15.(2022·山东济南期中)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有 ADCE中,DE的最小值是 .
(第15题) (第16题)
16.(2021·重庆渝中区月考)如图,等边三角形ABC的边长为6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t s,当以A,C,E,F为顶点的四边形是平行四边形时,
t= .
三、解答题(共6小题,共52分)
17.(6分)(2022·湖南长沙期中)如图,BD是平行四边形ABCD的一条对角线,过A,C两点作AE⊥BD,CF⊥BD,垂足分别为点E,F,延长线段AE,CF分别交边CD,AB于点M,N.求证:四边形CMAN是平行四边形.
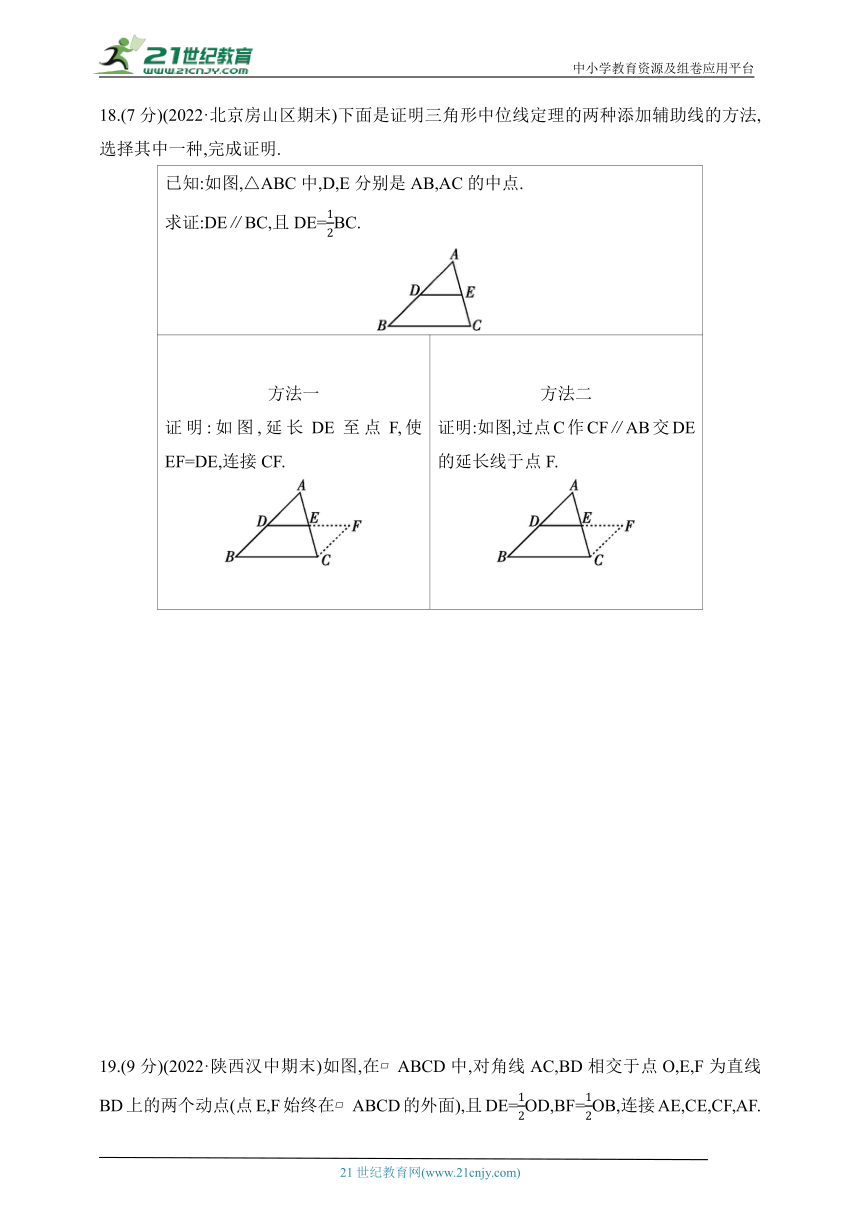
18.(7分)(2022·北京房山区期末)下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
已知:如图,△ABC中,D,E分别是AB,AC的中点. 求证:DE∥BC,且DE=BC.
方法一 证明:如图,延长DE至点F,使EF=DE,连接CF. 方法二 证明:如图,过点C作CF∥AB交DE的延长线于点F.
19.(9分)(2022·陕西汉中期末)如图,在 ABCD中,对角线AC,BD相交于点O,E,F为直线BD上的两个动点(点E,F始终在 ABCD的外面),且DE=OD,BF=OB,连接AE,CE,CF,AF.
(1)求证:四边形AFCE为平行四边形.
(2)若AC=6,EF=10,AF=4,求平行四边形AFCE的周长.
20.(9分)(2021·湖南长沙望城区期末)如图,根据下列对话,回答问题:
(1)多边形的内角和为2 022°,为什么不可能
(2)明明求的是几边形的内角和
21.(10分)(2021·浙江杭州余杭区期中)如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC.E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF.求证:ED=EF.
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形,并证明你的结论(请补全图形,再解答).
22.(11分)如图(1),Rt△ABC的直角边BC在直线l上,AB=6 cm,∠ACB=30°,∠ABC=90°.将Rt△ABC在直线l上向右平移得到Rt△DEF,连接AD,如图(2).
图(1) 图(2)
(1)求证:四边形ABED是平行四边形.
(2)如图(2),点E在边BC上,AC与DE交于点H.
①若四边形DHCF的面积是10 cm2,则四边形ABEH的面积为 cm2.
②当点E位于BC的中点处时,求四边形DHCF的面积.
(3)当点E与点C重合时,求Rt△ABC平移过程中扫过的面积.
第六章 平行四边形
1 2 3 4 5 6 7 8 9 10
D A C D B C B A A B
11.对角线互相平分的四边形是平行四边形
12.6 13.32 14.51° 15.3 16.2或6
1.D ∵点D,E分别为AB,AC的中点,BC=4,∴DE是△ABC的中位线,DE=BC=×4=2.
2.A ∵四边形ABCD是平行四边形,∴∠A=∠C,∠A+∠D=180°.∵∠A+∠C=120°,∴∠A=60°,∴∠D=180°-∠A=
120°.
3.C ∵平行四边形的对角线互相平分,∴AO=CO=AC=4,BO=DO=BD=5,∴根据三角形的三边关系,可得14.D 添加AB=CD,由“一组对边平行且相等的四边形是平行四边形”可判定四边形ABCD是平行四边形;添加AD∥BC,由“两组对边分别平行的四边形是平行四边形”可判定四边形ABCD是平行四边形;由AB∥CD可得∠BAO=∠DCO,∠ABO=∠CDO,结合OA=OC可证△ABO≌△CDO,所以AB=CD,由“一组对边平行且相等的四边形是平行四边形”可判定四边形ABCD是平行四边形;由AB∥CD,AD=BC无法判定四边形ABCD是平行四边形.故选D.
5.B ∵正多边形的内角和度数为(n-2)·180°,且每个内角都相等,∴正五边形的每个内角的度数为(5-2)·180°=108°,正六边形的每个内角的度数为(6-2)·
180°=120°,∴∠AOB=360°-108°-120°×2=12°.
6.C (转化思想)∵四边形ABCD是平行四边形,∴OB=OD,AB=CD,AD=BC.∵△AOB的周长与△AOD的周长之差为5,∴(OA+OB+AB)-(OA+OD+AD)=AB-AD=5.又AB=2AD,∴AB=
10,AD=5,∴ ABCD的周长=2(AB+AD)=30.
7.B 在平行四边形ABCD中,S△ABC=S ABCD.∵DE⊥AB,BF⊥AC,∴AC·BF=AB·DE.∵AB=6,AC=8,DE=4,∴8BF=
6×4,解得BF=3.
8.A 甲方案中,连接AC,∵四边形ABCD是平行四边形,∴AC经过BD的中点O,且AO=CO.∵BO=DO,BN=NO,OM=MD,∴NO=OM,∴四边形ANCM是平行四边形(对角线互相平分的四边形是平行四边形);乙方案中,显然可证得ABN≌△CDM,∴AN=CM.∵AN⊥BD,
CM⊥BD,∴AN∥CM,∴四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形);丙方案中,由平行四边形的性质及角平分线的性质可证BAN≌△DCM,
∴AN=CM,∠ANB=∠CMD,∴∠ANM=∠CMN,∴AN∥CM,∴四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形).综上可知,甲、乙、丙三种方案都是正确的.
9.A ∵四边形ABCD是平行四边形,∴BC∥AD,AD=BC,∴∠GBF=∠HDE.∵点E,F分别是平行四边形ABCD的边AD,BC的中点,∴BF=DE.在△GBF和△HDE中,
∴△GBF≌△HDE,∴GF=EH,∠BGF=∠DHE,∴∠FGH=∠EHG,∴GF∥EH,∴四边形EGFH是平行四边形,∴EG=FH.∵∠EHG不一定等于90°,∴EH⊥BD不正确,故选A.
10.B 如图,延长DM交AC于点E,∵AM平分∠CAD,AM⊥DM,∴∠DAM=∠EAM,∠AMD=
∠AME=90°.在△ADM和△AEM中,∴△ADM≌△AEM,∴DM=EM,AE=AD=
12,∴M是DE的中点.∵N是CD的中点,∴MN是△CDE的中位线.∵MN=2,∴CE=2MN=4,
∴AC=AE+CE=12+4=16,在平行四边形ABCD中,BC=AD=12,AC⊥BC,∴∠ACB=90°,
∴AB===20.
11.对角线互相平分的四边形是平行四边形
12.6 设这个多边形的边数为n,∵n边形的内角和为(n-2)×180°,多边形的外角和为360°,∴(n-2)×180°=360°×2,解得n=6,∴此多边形的边数是6.
13.32 由作法得BE平分∠ABC.∴∠ABE=∠CBE.∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD=AE+DE=5+3=8,AB=CD,∴∠CBE=∠AEB,∴∠ABE=∠AEB,∴AB=AE=5,∴CD=5.∵CE⊥DE,∴在Rt△CDE中,CE===4,∴ ABCD的面积为AD·CE=8×4=32.
14.51° ∵四边形ABCD是平行四边形,∠C=52°,∴∠A=∠C=52°.由翻折得∠BFE=∠A=52°,∠ABE=∠ABD.∵EF=DF,∴∠FED=∠EDF.由三角形外角的性质,得∠BFE=∠FED+∠EDF=2∠EDF,∴∠EDF=∠BFE=×52°=26°.在△ABD中,∠ABD=
180°-∠A-∠EDF=102°,∴∠ABE=∠ABD=51°.
15.3 ∵四边形ADCE是平行四边形,∴OD=OE,OA=OC.当OD取最小值时,线段DE最短,此时BC⊥DE.易知此时OD为△ABC的中位线,∴OD最小值=AB=,∴ED最小值=2OD最小值=3.
16.2或6 (分类讨论思想)根据题意,可以分以下两种情况讨论:①当点F在点C的左侧时,根据题意得AE=t cm,BF=2t cm,则CF=BC-BF=(6-2t)cm.∵AG∥BC,∴当AE=CF时,四边形AECF是平行四边形,即t=6-2t,解得t=2.②当点F在点C的右侧时,根据题意得AE=t cm,BF=2t cm,则CF=BF-BC=(2t-6)cm.∵AG∥BC,∴当AE=CF时,四边形AEFC是平行四边形,即t=2t-6,解得t=6.综上可得,当以A,C,E,F为顶点的四边形是平行四边形时,t=2或6.
17.【参考答案】证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN.
∵四边形ABCD是平行四边形,
∴CM∥AN,
∴四边形CMAN是平行四边形. (6分)
18.【参考答案】证明:选择方法一. (1分)
∵D,E分别是AB,AC的中点,
∴AD=BD,AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE,
∴∠ADE=∠F,AD=CF,
∴CF∥AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC. (7分)
证明:选择方法二. (1分)
∵D,E分别是AB,AC的中点,
∴AD=BD,AE=CE.
∵CF∥AB,
∴∠ADE=∠F.
在△ADE和△CFE中,
∴△ADE≌△CFE,
∴AD=CF,DE=FE,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC. (7分)
19.【参考答案】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵DE=OD,BF=OB,
∴DE=BF,
∴OD+DE=OB+BF,
即OE=OF,
∴四边形AFCE为平行四边形. (5分)
(2)∵OA=OC=AC=3,OE=OF=EF=5,AF=4,
∴OA2+AF2=OF2,
∴△AOF是直角三角形,∠OAF=90°,
∴在Rt△FAC中,CF===2.
∵四边形AFCE是平行四边形,
∴CE=AF=4,AE=CF=2,
∴平行四边形AFCE的周长=2(AF+CF)=8+4. (9分)
20.【参考答案】(1)设多边形的边数为n,
则180°(n-2)=2 022°,
解得n=13.
∵n为正整数,
∴多边形的内角和不可能为2 022°. (3分)
(2)设应加的内角为x,多加的外角为y,多边形的边为m,
依题意可列方程180°(m-2)=2 022°+x-y,
∵-180°∴2 022°-180°<180°(m-2)<2 022°+180°,
∴12∵m为正整数,
∴m=13或m=14,
故明明求的是十三边形或十四边形的内角和. (9分)
21.【参考答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵AD=AC,AD⊥AC,
∴AC=BC,AC⊥BC.
如图(1),连接CE,∵E是AB的中点,
∴AE=EC,CE⊥AB,
∴∠ACE=∠BCE=45°,
∴∠ECF=∠EAD=135°.
∵ED⊥EF,
∴∠CEF=∠AED=90°-∠CED. (4分)
在△CEF和△AED中,
∴△CEF≌△AED,
∴ED=EF. (6分)
(2)四边形ACPE是平行四边形.
证明:如图(2),连接CE,由(1)得△CEF≌△AED,
∴CF=AD.
∵AD=AC,
∴AC=CF. (8分)
∵DP∥AB,
∴CP是△ABF的中位线,
∴CP=AB=AE,
∴四边形ACPE是平行四边形. (10分)
22.
(1)平移的性质AD BE即可得证
(2)①S△HEC+S四边形ABEH=S四边形DHCF+S△HECS四边形ABEH=
S四边形DHCF
②根据S△HEC+S四边形DHCF=S△DEF=S△ABCS四边形DHCF
(3)Rt△ABC平移过程中扫过的面积=S ABED+S△DEF
【参考答案】(1)证明:由平移的性质可得,
AD=BE,AD∥BE,
故四边形ABED是平行四边形. (2分)
(2)①10 (3分)
②由AB=6 cm,∠ACB=30°,∠ABC=90°,
可得AC=12 cm,
根据勾股定理,
可得BC==6 cm.
∵点E位于BC的中点处,
∴BE=CE=3 cm,
此时EH为Rt△ABC的中位线,
即HE=3 cm,
故S△HEC=3×3×=(cm2),
故S四边形DHCF=S△DEF-S△HEC
=6×6×-
=(cm2). (8分)
(3)当点E与点C重合时,
Rt△ABC平移过程中扫过的面积为
S ABED+S△DEF
=6×6+6×6×
=54(cm2). (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版数学八年级下学期
第六章 平行四边形
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·广东中考)如图,在△ABC中,BC=4,点D,E分别为AB,AC的中点,则DE= ( )
A. B.
C.1 D.2
(第1题) (第2题)
2.(2022·福建南平期末)如图,在平行四边形ABCD中,若∠A+∠C=120°,则∠D的度数为( )
A.120° B.60°
C.30° D.150°
3.(2022·四川凉山期末)如图,在平行四边形ABCD中,AC,BD相交于点O,AC=8,BD=10,则AD的长的取值范围是 ( )
A.AD>1 B.AD<9
C.1
(第3题) (第4题)
4.(2021·山西模拟改编)如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判定四边形ABCD是平行四边形的是 ( )
A.AB=CD B.AD∥BC
C.OA=OC D.AD=BC
5.[贴近校园生活](2022·山东济南期末)足球表面为什么由正六边形和正五边形构成 因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角,而又不足一个周角.这样,由平面折叠而成的多面体充气后最终就呈现为球形.如图,在折叠前的平面上,拼接点处的缝隙∠AOB的大小为 ( )
A.10° B.12° C.14° D.16°
6.(2021·重庆期末)如图,△AOB与△AOD的周长之差为5,且AB=2AD,则 ABCD的周长是( )
A.15 B.20 C.30 D.40
(第6题) (第7题)
7.(2022·四川乐山中考)如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为 ( )
A.4 B.3 C. D.2
8.(2021·河北中考)如图(1), ABCD中,AD>AB,∠ABC为锐角,要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图(2)中的甲、乙、丙三种方案,则正确的方案( )
取BD中点O,作BN=NO,OM=MD
作CM⊥BD于M,AN⊥BD于N
作AN,CM分别平分∠BAD,∠BCD
图(1) 图(2)
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
9.(2022·河北保定期末)如图,点E,F分别是 ABCD的边AD,BC的中点,点G,H是对角线BD上的两点,且BG=DH,连接HE,HF,GF,GE,则下列结论中不正确的是 ( )
A.EH⊥BD
B.四边形EGFH是平行四边形
C.EG=FH
D.GF∥EH
(第9题) (第10题)
10.(2022·广东茂名期末)如图,在平行四边形ABCD中,AC⊥BC,点M在∠CAD的平分线上,且AM⊥DM,N为CD的中点,连接MN.若AD=12,MN=2,则AB的长为( )
A.12 B.20 C.24 D.30
二、填空题(共6小题,每小题3分,共18分)
11.小玲的爸爸在做平行四边形框架时,采用如下方法:如图,将两根木条AC,BD的中点O重叠并用钉子固定,然后用木条将AB,BC,CD,DA分别钉起来,则四边形ABCD就是平行四边形,这种做法的依据是 .
12.(2022·江苏南京模拟)已知一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数是 .
13.(2021·江苏苏州期末)如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以F,G为圆心,大于FG的长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥DE,AE=5,DE=3,则 ABCD的面积为 .
(第13题) (第14题)
14.如图,点E为 ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE等于 .
15.(2022·山东济南期中)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有 ADCE中,DE的最小值是 .
(第15题) (第16题)
16.(2021·重庆渝中区月考)如图,等边三角形ABC的边长为6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t s,当以A,C,E,F为顶点的四边形是平行四边形时,
t= .
三、解答题(共6小题,共52分)
17.(6分)(2022·湖南长沙期中)如图,BD是平行四边形ABCD的一条对角线,过A,C两点作AE⊥BD,CF⊥BD,垂足分别为点E,F,延长线段AE,CF分别交边CD,AB于点M,N.求证:四边形CMAN是平行四边形.
18.(7分)(2022·北京房山区期末)下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
已知:如图,△ABC中,D,E分别是AB,AC的中点. 求证:DE∥BC,且DE=BC.
方法一 证明:如图,延长DE至点F,使EF=DE,连接CF. 方法二 证明:如图,过点C作CF∥AB交DE的延长线于点F.
19.(9分)(2022·陕西汉中期末)如图,在 ABCD中,对角线AC,BD相交于点O,E,F为直线BD上的两个动点(点E,F始终在 ABCD的外面),且DE=OD,BF=OB,连接AE,CE,CF,AF.
(1)求证:四边形AFCE为平行四边形.
(2)若AC=6,EF=10,AF=4,求平行四边形AFCE的周长.
20.(9分)(2021·湖南长沙望城区期末)如图,根据下列对话,回答问题:
(1)多边形的内角和为2 022°,为什么不可能
(2)明明求的是几边形的内角和
21.(10分)(2021·浙江杭州余杭区期中)如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC.E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF.求证:ED=EF.
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形,并证明你的结论(请补全图形,再解答).
22.(11分)如图(1),Rt△ABC的直角边BC在直线l上,AB=6 cm,∠ACB=30°,∠ABC=90°.将Rt△ABC在直线l上向右平移得到Rt△DEF,连接AD,如图(2).
图(1) 图(2)
(1)求证:四边形ABED是平行四边形.
(2)如图(2),点E在边BC上,AC与DE交于点H.
①若四边形DHCF的面积是10 cm2,则四边形ABEH的面积为 cm2.
②当点E位于BC的中点处时,求四边形DHCF的面积.
(3)当点E与点C重合时,求Rt△ABC平移过程中扫过的面积.
第六章 平行四边形
1 2 3 4 5 6 7 8 9 10
D A C D B C B A A B
11.对角线互相平分的四边形是平行四边形
12.6 13.32 14.51° 15.3 16.2或6
1.D ∵点D,E分别为AB,AC的中点,BC=4,∴DE是△ABC的中位线,DE=BC=×4=2.
2.A ∵四边形ABCD是平行四边形,∴∠A=∠C,∠A+∠D=180°.∵∠A+∠C=120°,∴∠A=60°,∴∠D=180°-∠A=
120°.
3.C ∵平行四边形的对角线互相平分,∴AO=CO=AC=4,BO=DO=BD=5,∴根据三角形的三边关系,可得1
5.B ∵正多边形的内角和度数为(n-2)·180°,且每个内角都相等,∴正五边形的每个内角的度数为(5-2)·180°=108°,正六边形的每个内角的度数为(6-2)·
180°=120°,∴∠AOB=360°-108°-120°×2=12°.
6.C (转化思想)∵四边形ABCD是平行四边形,∴OB=OD,AB=CD,AD=BC.∵△AOB的周长与△AOD的周长之差为5,∴(OA+OB+AB)-(OA+OD+AD)=AB-AD=5.又AB=2AD,∴AB=
10,AD=5,∴ ABCD的周长=2(AB+AD)=30.
7.B 在平行四边形ABCD中,S△ABC=S ABCD.∵DE⊥AB,BF⊥AC,∴AC·BF=AB·DE.∵AB=6,AC=8,DE=4,∴8BF=
6×4,解得BF=3.
8.A 甲方案中,连接AC,∵四边形ABCD是平行四边形,∴AC经过BD的中点O,且AO=CO.∵BO=DO,BN=NO,OM=MD,∴NO=OM,∴四边形ANCM是平行四边形(对角线互相平分的四边形是平行四边形);乙方案中,显然可证得ABN≌△CDM,∴AN=CM.∵AN⊥BD,
CM⊥BD,∴AN∥CM,∴四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形);丙方案中,由平行四边形的性质及角平分线的性质可证BAN≌△DCM,
∴AN=CM,∠ANB=∠CMD,∴∠ANM=∠CMN,∴AN∥CM,∴四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形).综上可知,甲、乙、丙三种方案都是正确的.
9.A ∵四边形ABCD是平行四边形,∴BC∥AD,AD=BC,∴∠GBF=∠HDE.∵点E,F分别是平行四边形ABCD的边AD,BC的中点,∴BF=DE.在△GBF和△HDE中,
∴△GBF≌△HDE,∴GF=EH,∠BGF=∠DHE,∴∠FGH=∠EHG,∴GF∥EH,∴四边形EGFH是平行四边形,∴EG=FH.∵∠EHG不一定等于90°,∴EH⊥BD不正确,故选A.
10.B 如图,延长DM交AC于点E,∵AM平分∠CAD,AM⊥DM,∴∠DAM=∠EAM,∠AMD=
∠AME=90°.在△ADM和△AEM中,∴△ADM≌△AEM,∴DM=EM,AE=AD=
12,∴M是DE的中点.∵N是CD的中点,∴MN是△CDE的中位线.∵MN=2,∴CE=2MN=4,
∴AC=AE+CE=12+4=16,在平行四边形ABCD中,BC=AD=12,AC⊥BC,∴∠ACB=90°,
∴AB===20.
11.对角线互相平分的四边形是平行四边形
12.6 设这个多边形的边数为n,∵n边形的内角和为(n-2)×180°,多边形的外角和为360°,∴(n-2)×180°=360°×2,解得n=6,∴此多边形的边数是6.
13.32 由作法得BE平分∠ABC.∴∠ABE=∠CBE.∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD=AE+DE=5+3=8,AB=CD,∴∠CBE=∠AEB,∴∠ABE=∠AEB,∴AB=AE=5,∴CD=5.∵CE⊥DE,∴在Rt△CDE中,CE===4,∴ ABCD的面积为AD·CE=8×4=32.
14.51° ∵四边形ABCD是平行四边形,∠C=52°,∴∠A=∠C=52°.由翻折得∠BFE=∠A=52°,∠ABE=∠ABD.∵EF=DF,∴∠FED=∠EDF.由三角形外角的性质,得∠BFE=∠FED+∠EDF=2∠EDF,∴∠EDF=∠BFE=×52°=26°.在△ABD中,∠ABD=
180°-∠A-∠EDF=102°,∴∠ABE=∠ABD=51°.
15.3 ∵四边形ADCE是平行四边形,∴OD=OE,OA=OC.当OD取最小值时,线段DE最短,此时BC⊥DE.易知此时OD为△ABC的中位线,∴OD最小值=AB=,∴ED最小值=2OD最小值=3.
16.2或6 (分类讨论思想)根据题意,可以分以下两种情况讨论:①当点F在点C的左侧时,根据题意得AE=t cm,BF=2t cm,则CF=BC-BF=(6-2t)cm.∵AG∥BC,∴当AE=CF时,四边形AECF是平行四边形,即t=6-2t,解得t=2.②当点F在点C的右侧时,根据题意得AE=t cm,BF=2t cm,则CF=BF-BC=(2t-6)cm.∵AG∥BC,∴当AE=CF时,四边形AEFC是平行四边形,即t=2t-6,解得t=6.综上可得,当以A,C,E,F为顶点的四边形是平行四边形时,t=2或6.
17.【参考答案】证明:∵AE⊥BD,CF⊥BD,
∴AM∥CN.
∵四边形ABCD是平行四边形,
∴CM∥AN,
∴四边形CMAN是平行四边形. (6分)
18.【参考答案】证明:选择方法一. (1分)
∵D,E分别是AB,AC的中点,
∴AD=BD,AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE,
∴∠ADE=∠F,AD=CF,
∴CF∥AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC. (7分)
证明:选择方法二. (1分)
∵D,E分别是AB,AC的中点,
∴AD=BD,AE=CE.
∵CF∥AB,
∴∠ADE=∠F.
在△ADE和△CFE中,
∴△ADE≌△CFE,
∴AD=CF,DE=FE,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC. (7分)
19.【参考答案】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵DE=OD,BF=OB,
∴DE=BF,
∴OD+DE=OB+BF,
即OE=OF,
∴四边形AFCE为平行四边形. (5分)
(2)∵OA=OC=AC=3,OE=OF=EF=5,AF=4,
∴OA2+AF2=OF2,
∴△AOF是直角三角形,∠OAF=90°,
∴在Rt△FAC中,CF===2.
∵四边形AFCE是平行四边形,
∴CE=AF=4,AE=CF=2,
∴平行四边形AFCE的周长=2(AF+CF)=8+4. (9分)
20.【参考答案】(1)设多边形的边数为n,
则180°(n-2)=2 022°,
解得n=13.
∵n为正整数,
∴多边形的内角和不可能为2 022°. (3分)
(2)设应加的内角为x,多加的外角为y,多边形的边为m,
依题意可列方程180°(m-2)=2 022°+x-y,
∵-180°
∴12
∴m=13或m=14,
故明明求的是十三边形或十四边形的内角和. (9分)
21.【参考答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵AD=AC,AD⊥AC,
∴AC=BC,AC⊥BC.
如图(1),连接CE,∵E是AB的中点,
∴AE=EC,CE⊥AB,
∴∠ACE=∠BCE=45°,
∴∠ECF=∠EAD=135°.
∵ED⊥EF,
∴∠CEF=∠AED=90°-∠CED. (4分)
在△CEF和△AED中,
∴△CEF≌△AED,
∴ED=EF. (6分)
(2)四边形ACPE是平行四边形.
证明:如图(2),连接CE,由(1)得△CEF≌△AED,
∴CF=AD.
∵AD=AC,
∴AC=CF. (8分)
∵DP∥AB,
∴CP是△ABF的中位线,
∴CP=AB=AE,
∴四边形ACPE是平行四边形. (10分)
22.
(1)平移的性质AD BE即可得证
(2)①S△HEC+S四边形ABEH=S四边形DHCF+S△HECS四边形ABEH=
S四边形DHCF
②根据S△HEC+S四边形DHCF=S△DEF=S△ABCS四边形DHCF
(3)Rt△ABC平移过程中扫过的面积=S ABED+S△DEF
【参考答案】(1)证明:由平移的性质可得,
AD=BE,AD∥BE,
故四边形ABED是平行四边形. (2分)
(2)①10 (3分)
②由AB=6 cm,∠ACB=30°,∠ABC=90°,
可得AC=12 cm,
根据勾股定理,
可得BC==6 cm.
∵点E位于BC的中点处,
∴BE=CE=3 cm,
此时EH为Rt△ABC的中位线,
即HE=3 cm,
故S△HEC=3×3×=(cm2),
故S四边形DHCF=S△DEF-S△HEC
=6×6×-
=(cm2). (8分)
(3)当点E与点C重合时,
Rt△ABC平移过程中扫过的面积为
S ABED+S△DEF
=6×6+6×6×
=54(cm2). (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
