第19章 四边形单元测试题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版数学八年级下学期
第19章 四边形
时间:60分钟 满分:100分
题号 一 二 三 评价
错题
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
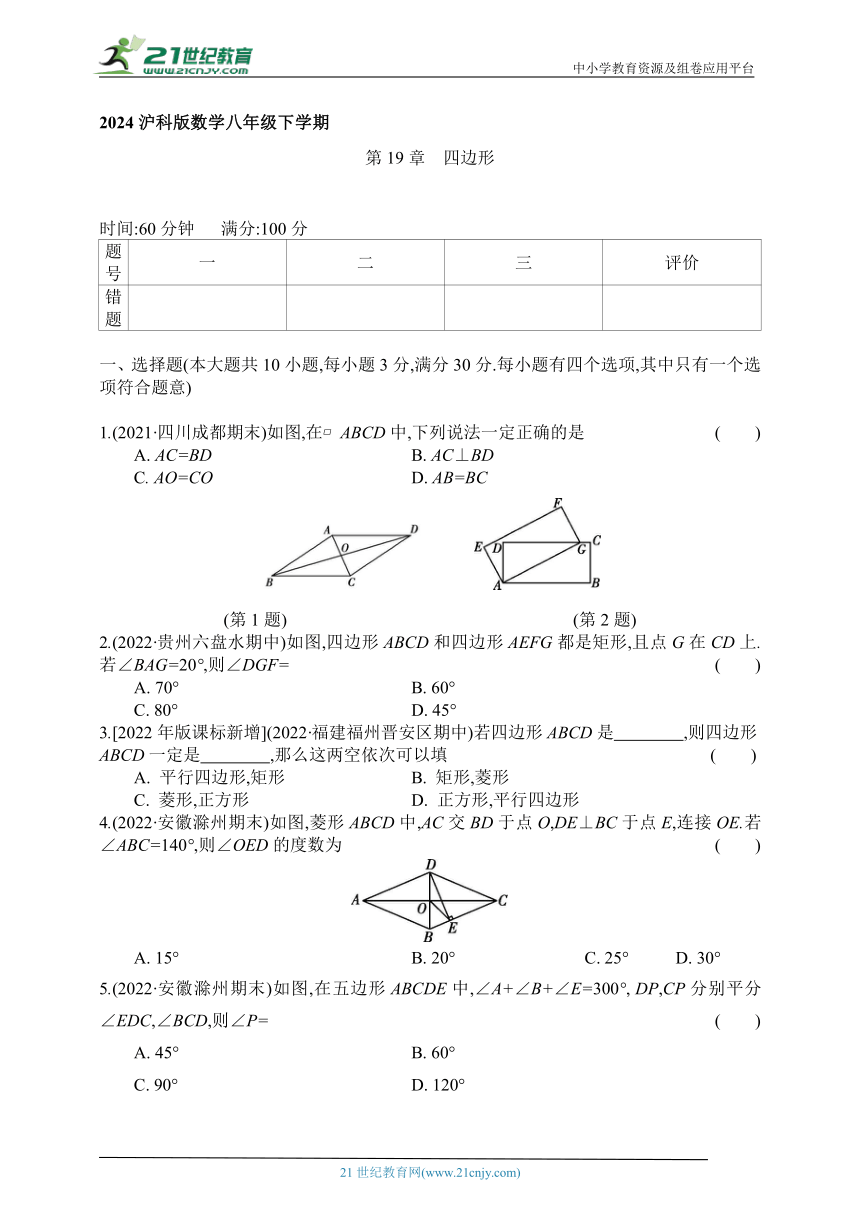
1.(2021·四川成都期末)如图,在 ABCD中,下列说法一定正确的是 ( )
A. AC=BD B. AC⊥BD
C. AO=CO D. AB=BC
(第1题) (第2题)
2.(2022·贵州六盘水期中)如图,四边形ABCD和四边形AEFG都是矩形,且点G在CD上.若∠BAG=20°,则∠DGF= ( )
A. 70° B. 60°
C. 80° D. 45°
3.[2022年版课标新增](2022·福建福州晋安区期中)若四边形ABCD是 ,则四边形ABCD一定是 ,那么这两空依次可以填 ( )
A. 平行四边形,矩形 B. 矩形,菱形
C. 菱形,正方形 D. 正方形,平行四边形
4.(2022·安徽滁州期末)如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE.若∠ABC=140°,则∠OED的度数为 ( )
A. 15° B. 20° C. 25° D. 30°
5.(2022·安徽滁州期末)如图,在五边形ABCDE中,∠A+∠B+∠E=300°, DP,CP分别平分∠EDC,∠BCD,则∠P= ( )
A. 45° B. 60°
C. 90° D. 120°
(第5题) (第6题)
6.(2022·江苏南京模拟)如图,以正方形ABCD的一边AD为边向外作等边三角形ADE,则∠BED的度数是 ( )
A. 30° B. 36°
C. 45° D. 52°
7.(2022·北京东城区期中)如图,点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.则下列说法中正确的是 ( )
A. 若AC=BD,则四边形EFGH为矩形
B. 若AC⊥BD,则四边形EFGH为菱形
C. 若四边形EFGH是平行四边形,则AC与BD互相平分
D. 若四边形EFGH是正方形,则AC与BD互相垂直且相等
(第7题) (第8题)
8.如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E,F.连接EF,则线段EF的长的最小值为 ( )
A. B.
C. D.
9.(2022·山东济南槐荫区一模)四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC'D',如果∠DAD'=30°,那么菱形ABC'D'与正方形ABCD的面积之比是 ( )
A. B.
C. D. 1
(第9题) (第10题)
10.(2022·江苏连云港期末)如图,矩形ABCD中,AB=9,BC=12,点F在CD上,且DF=5,E是BC边上的一动点,M,N分别是AE,EF的中点,则在点E从B向C运动的整个过程中,线段MN所扫过的区域面积是 ( )
A. 13 B. 14
C. 15 D. 16
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(2022·江苏南京模拟)已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件: ,使四边形ABCD是平行四边形.
12.(2021·广西南宁二中三模)如图,四边形ABCD是菱形,E,F分别是AD,BD的中点.若EF=2,则BC的长为 .
(第12题) (第13题)
13.(2022·云南昆明呈贡区一模)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=4,AD=8,则四边形ABOM的周长为 .
14.(2022·山东东营期末)如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为 米.
(第14题) (第15题)
15.如图,正方形ABCD的边长为1,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH…如此下去,第n个正方形的边长为 .
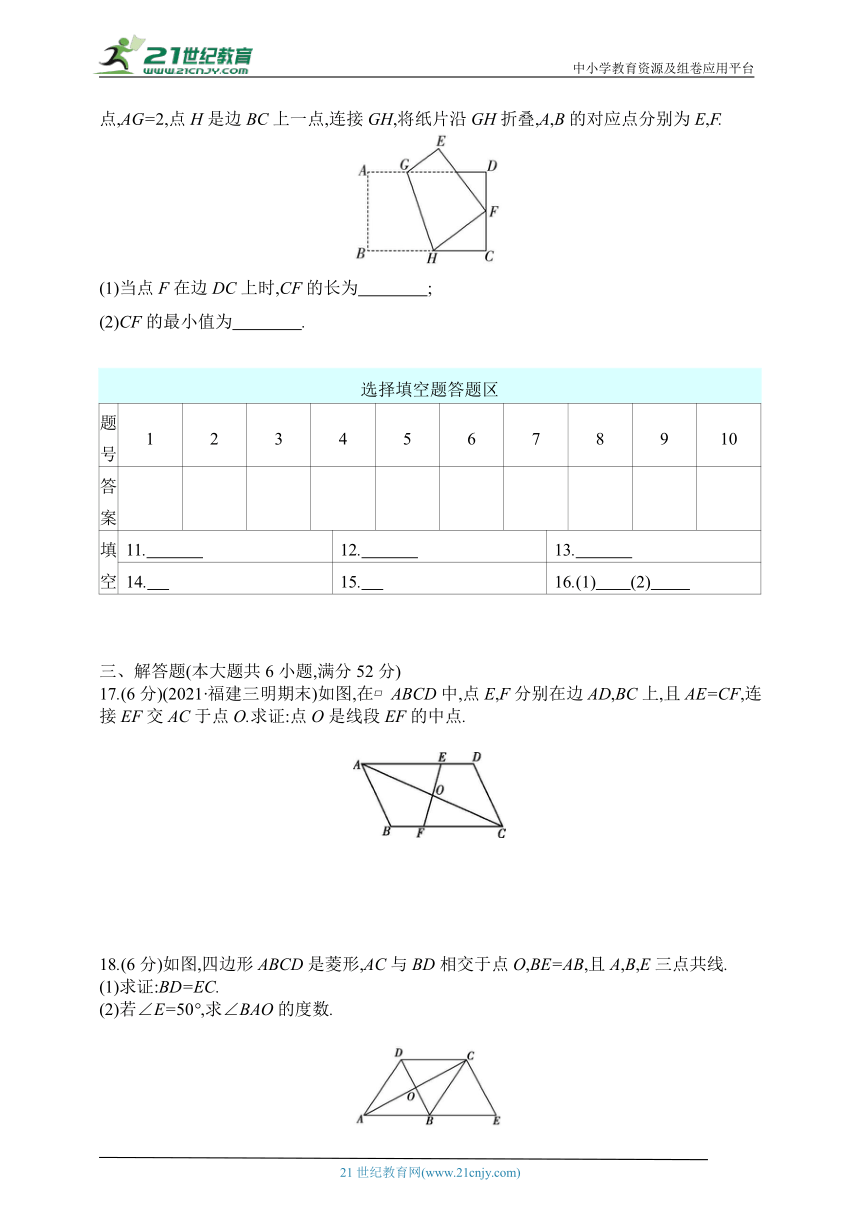
16.(2022·安徽合肥庐阳区期末)如图,矩形纸片ABCD中,AB=4,AD=6,点G是边AD上的点,AG=2,点H是边BC上一点,连接GH,将纸片沿GH折叠,A,B的对应点分别为E,F.
(1)当点F在边DC上时,CF的长为 ;
(2)CF的最小值为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.(1) (2)
三、解答题(本大题共6小题,满分52分)
17.(6分)(2021·福建三明期末)如图,在 ABCD中,点E,F分别在边AD,BC上,且AE=CF,连接EF交AC于点O.求证:点O是线段EF的中点.
18.(6分)如图,四边形ABCD是菱形,AC与BD相交于点O,BE=AB,且A,B,E三点共线.
(1)求证:BD=EC.
(2)若∠E=50°,求∠BAO的度数.
19.(8分) (2022·河南许昌建安区期中)在数学课上,老师提出如下问题:如图,在Rt△ABC中,∠ABC=90°.求作:矩形ABCD.
小东的作法如下:
①作线段AC的垂直平分线交AC于点O;
②连接BO并延长,在延长线上截取OD=OB;
③连接AD,CD.
则四边形ABCD即为所求作的矩形.
(1)使用直尺和圆规,依据小东的作法补全图形;(保留作图痕迹)
(2)完成下边的证明.
证明:∵OA= ,OD=OB,
∴四边形ABCD是平行四边形( ).
(填依据)
∵∠ABC=90°,
∴四边形ABCD是矩形( ).(填依据)
20.(10分)(2021·山东滨州一模)如图,P是正方形ABCD对角线BD上的一点,PE⊥BC于点E,PF⊥CD于点F.
(1)求证:PA=EF.
(2)若正方形ABCD的边长为12,求四边形PFCE的周长.
21.(10分)如图(1),在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,连接P C.
(1)求∠CPE的度数;
(2)把正方形ABCD改为菱形ABCD,其他条件不变,如图(2),当∠ABC=120°时,连接CE,试探究线段AP与线段CE之间的数量关系,并说明理由.
图(1) 图(2)
22.(12分)在四边形ABCD中,对角线AC,BD相交于点O,过点O的两条直线分别交边AB,CD,AD,BC于点E,F,G,H.
(1)感知
如图(1),若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;
(2)拓展
如图(2),若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a,b,m的代数式表示);
(3)探究
如图(3),若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F,G,H的位置,使直线EF,GH把平行四边形ABCD的面积四等分.
图(1) 图(2) 图(3)
第19章 四边形
1 2 3 4 5 6 7 8 9 10
C A D B B C D D A C
11.AB=CD(答案不唯一) 12.4 13.10+2
14.80 15.()n-1 16.(1)2 (2)4-2
1.C 【关键】平行四边形的对角线互相平分
2.A ∵四边形ABCD和四边形AEFG都是矩形,∴∠FGA=90°,CD∥AB,∴∠DGA=∠BAG=20°,∴∠DGF=90°-∠DGA=90°-20°=70°.
3.D 若四边形ABCD是正方形,则四边形ABCD一定是平行四边形.
4.B ∵四边形ABCD是菱形,∠ABC=140°,∴∠ABD=∠CBD=∠ABC=70°,BO=DO.∵DE⊥BC,∴OE=OD=OB,∠BDE=20°,
∴∠OED=∠ODE=20°.
5.B ∵∠A+∠B+∠E=300°,∴∠EDC+∠BCD=(5-2)×180°-300°=240°.又DP,CP分别平分∠EDC,∠BCD,∴∠PDC+
∠PCD=120°,∴∠P=180°-(∠PDC+∠PCD)=180°-120°=60°.
6.C ∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°.∵△ADE是等边三角形,∴AD=AE,∠DAE=∠AED=60°,∴∠BAE=
150°,AB=AE,∴∠AEB=15°,∴∠BED=60°-15°=45°.
7.D (排除法)∵点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,∴EH=BD=FG,EH∥BD∥FG,∴四边形EFGH是平行四边形.由AC=BD可得EH=EF,∴四边形EFGH为菱形,A选项错误;由AC⊥BD,可得EH⊥EF,∴四边形EFGH为矩形,B选项错误.由四边形EFGH是平行四边形,无法得到AC与BD互相平分,C选项错误.故选D.
8.D 连接CD,∵DE⊥BC,DF⊥AC,∠ACB=90°,∴四边形CEDF是矩形,∴EF=CD.当CD⊥AB时,CD的长有最小值,即此时线段EF的长有最小值.∵AC=3,BC=4,∴AB==5.当CD⊥AB时,S△ABC=AB·CD=AC·BC,∴CD==,即线段EF的长的最小值为.
9.A 如图,过点D'作D'M⊥AB于点M,则∠D'MA=90°.∵四边形ABCD是正方形,∴正方形ABCD的面积=AB2.∵∠DAD'
=30°,∴∠D'AM=60°,∠AD'M=30°.在Rt△D'AM中,由勾股定理可得D'M=AD'.∵四边形ABC'D'是菱形,∴AD'=AB,即D'M=AB,∴菱形ABC'D'的面积=AB×D'M=AB2,∴菱形ABC'D'与正方形ABCD的面积之比==.
10.C 如图,当点E与点B重合时,点M位于AB的中点,点N位于BF的中点;当点E与点C重合时,点M(记为M')位于AC的中点,点N(记为N')位于FC的中点.连接MN,MM',NN',M'N'.∵M是AB的中点,M'是AC的中点,N是BF的中点,N'是FC的中点,∴MM',NN'分别是△ABC,△FBC的中位线,∴MM'∥BC且MM'=BC,NN'∥BC且NN'=BC,∴四边形MM'N'N为平行四边形,∴线段MN所扫过的区域为平行四边形.∵四边形ABCD是矩形,∴CD=AB=9.∵DF=5,∴FC=9-5=4,∴S平行四边形MM'N'N=BC·(AB-FC)=×12×(×9-×4)=15.
11.AB=CD(答案不唯一,或AD∥BC等)
12.4 ∵E,F分别是AD,BD的中点,∴AB=2EF=4.∵四边形ABCD是菱形,∴BC=AB=4.
13.10+2 ∵四边形ABCD是矩形,∴BC=AD=8,CD=AB=4,∠ABC=90°,∴AC==4.∵O是AC的中点,∴BO=AC=2.∵AO=OC,AM=MD=4,∴OM=CD=2,∴四边形ABOM的周长为AB+OB+OM+AM=
4+2+2+4=10+2.
14.80 由题意可知,小明所走的路线是正多边形,∵360°÷45°=8,∴该正多边形是正八边形,故小明所走的路程为8×10=80(米).
15.()n-1 ∵四边形ABCD为正方形,∴AB=BC=1,∠B=90°,∴AC2=AB2+BC2=12+12,∴AC=.同理可求得AE=()2,AG=()3,…,∴第n个正方形的边长为()n-1.
16.(1)2 (2)4-2 (1)由题意得CD=AB=4,如图(1),作GM⊥BC于点M,GN⊥HF于点N,连接GF,则四边形GMCD为矩形,∴GM=CD=4.由折叠可知∠GHB=∠GHF,GE=AG=2.∵GM⊥BC,GN⊥HF,∴GN=GM=4.又GD=AD-AG=6-2=4,∴GD=GN.在Rt△GDF和Rt△GNF中,∴Rt△GDF≌Rt△GNF,∴DF=NF.∵∠E=∠EFN=∠GNF=90°,∴四边形GNFE为矩形,∴NF=GE=2,∴DF=NF=2,∴CF=CD-DF=4-2=2.(2)如图(2),连接CG,GF,由勾股定理得GF=
==2.∵DG=4,∴CG==4.在△CFG中,∵CF≥CG-GF,∴CF≥4-2,∴CF的最小值为4-2.
图(1) 图(2)
17.证明:证法一 如图,连接AF,CE.
∵ABCD为平行四边形,∴AE∥FC.
又AE=CF,
∴四边形AECF是平行四边形, (4分)
∴OE=OF,∴点O是线段EF的中点. (6分)
证法二 ∵ABCD为平行四边形,
∴AD∥BC,∴∠EAO=∠FCO. (2分)
在△AOE和△COF中,
∴△AOE≌△COF,∴OE=OF, (5分)
即点O是线段EF的中点. (6分)
18.解:(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD.
又BE=AB,A,B,E三点共线,
∴BE=CD,BE∥CD, (2分)
∴四边形BECD是平行四边形,
∴BD=EC. (3分)
(2)∵四边形BECD是平行四边形,
∴BD∥CE,∴∠ABO=∠E=50°. (4分)
∵四边形ABCD是菱形,∴AC⊥BD,
∴∠BAO=90°-∠ABO=90°-50°=40°. (6分)
19.解:(1)如图,矩形ABCD即为所求.
(5分)
(2)OC (6分)
对角线互相平分的四边形是平行四边形 (7分)
有一个角是直角的平行四边形是矩形 (8分)
20.解:(1)证明:如图,连接PC.
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠BCD=90°.
在△ABP与△CBP中,
∴△ABP≌△CBP,∴PA=PC.
∵PE⊥BC,PF⊥CD,
∠BCD=90°, (4分)
∴四边形PFCE是矩形,
∴EF=PC,∴PA=EF. (5分)
(2)由(1)知四边形PFCE是矩形,
∴PE=CF,PF=CE.
∵∠CBD=45°,∠PEB=90°,
∴∠BPE=45°,∴BE=PE. (7分)
由题意可知BC=12,
∴矩形PFCE的周长=2(PE+EC)=2(BE+EC)=2BC=24. (10分)
21.解:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADP=∠CDP=45°.
又PD=PD,
∴△ADP≌△CDP,∴∠DAP=∠DCP.
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPE=∠EDF=90°. (4分)
(2)AP=CE. (5分)
理由:∵四边形ABCD是菱形,∠ABC=120°,
∴AB=BC,∠ABP=∠CBP=60°.
又PB=PB,∴△ABP≌△CBP,
∴PA=PC,∠BAP=∠BCP,
∴∠DAP=∠DCP.
∵PA=PE,∴PC=PE,∠DAP=∠AEP,
∴∠DCP=∠AEP.
∵∠CFP=∠EFD,
∴180°-∠CFP-∠PCF=180°-∠EFD-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,∴AP=CE. (10分)
22.解:(1) (2分)
(2)在题图(2)中,过点O分别作ON⊥AD于点N,OM⊥AB于点M,
则OM=AD=b,ON=AB=a.
∵S△AOB=S矩形ABCD,S四边形AEOG=S矩形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,
即S△BOE=S△AOG.
∵S△BOE=BE·OM=m·b=mb,
S△AOG=AG·ON=AG·a=AG·a,
∴mb=AG·a,
∴AG=. (7分)
(3)在题图(3)中,过点O分别作OK⊥AB于点K,OQ⊥AD于点Q,并分别延长KO,QO交CD,BC于点L,P.
易得KL=2OK,PQ=2OQ.
∵S平行四边形ABCD=AB·KL=AD·PQ,
∴3×2OK=5×2OQ,
∴=.
∵S△AOB=S平行四边形ABCD,
S四边形AEOG=S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,
∴S△BOE=S△AOG.
∵S△BOE=BE·OK=×1×OK,S△AOG=AG·OQ,
∴×1×OK=AG·OQ,
∴AG==.
易证△AOG≌△COH,△BOE≌△DOF,
∴CH=AG=,DF=BE=1.
∴当点G到点A的距离、点H到点C的距离均为,点F到点D的距离为1时,直线EF,GH把平行四边形ABCD的面积四等分. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版数学八年级下学期
第19章 四边形
时间:60分钟 满分:100分
题号 一 二 三 评价
错题
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2021·四川成都期末)如图,在 ABCD中,下列说法一定正确的是 ( )
A. AC=BD B. AC⊥BD
C. AO=CO D. AB=BC
(第1题) (第2题)
2.(2022·贵州六盘水期中)如图,四边形ABCD和四边形AEFG都是矩形,且点G在CD上.若∠BAG=20°,则∠DGF= ( )
A. 70° B. 60°
C. 80° D. 45°
3.[2022年版课标新增](2022·福建福州晋安区期中)若四边形ABCD是 ,则四边形ABCD一定是 ,那么这两空依次可以填 ( )
A. 平行四边形,矩形 B. 矩形,菱形
C. 菱形,正方形 D. 正方形,平行四边形
4.(2022·安徽滁州期末)如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE.若∠ABC=140°,则∠OED的度数为 ( )
A. 15° B. 20° C. 25° D. 30°
5.(2022·安徽滁州期末)如图,在五边形ABCDE中,∠A+∠B+∠E=300°, DP,CP分别平分∠EDC,∠BCD,则∠P= ( )
A. 45° B. 60°
C. 90° D. 120°
(第5题) (第6题)
6.(2022·江苏南京模拟)如图,以正方形ABCD的一边AD为边向外作等边三角形ADE,则∠BED的度数是 ( )
A. 30° B. 36°
C. 45° D. 52°
7.(2022·北京东城区期中)如图,点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.则下列说法中正确的是 ( )
A. 若AC=BD,则四边形EFGH为矩形
B. 若AC⊥BD,则四边形EFGH为菱形
C. 若四边形EFGH是平行四边形,则AC与BD互相平分
D. 若四边形EFGH是正方形,则AC与BD互相垂直且相等
(第7题) (第8题)
8.如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E,F.连接EF,则线段EF的长的最小值为 ( )
A. B.
C. D.
9.(2022·山东济南槐荫区一模)四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC'D',如果∠DAD'=30°,那么菱形ABC'D'与正方形ABCD的面积之比是 ( )
A. B.
C. D. 1
(第9题) (第10题)
10.(2022·江苏连云港期末)如图,矩形ABCD中,AB=9,BC=12,点F在CD上,且DF=5,E是BC边上的一动点,M,N分别是AE,EF的中点,则在点E从B向C运动的整个过程中,线段MN所扫过的区域面积是 ( )
A. 13 B. 14
C. 15 D. 16
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(2022·江苏南京模拟)已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件: ,使四边形ABCD是平行四边形.
12.(2021·广西南宁二中三模)如图,四边形ABCD是菱形,E,F分别是AD,BD的中点.若EF=2,则BC的长为 .
(第12题) (第13题)
13.(2022·云南昆明呈贡区一模)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=4,AD=8,则四边形ABOM的周长为 .
14.(2022·山东东营期末)如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为 米.
(第14题) (第15题)
15.如图,正方形ABCD的边长为1,以对角线AC为边作第2个正方形ACEF,再以对角线AE为边作第3个正方形AEGH…如此下去,第n个正方形的边长为 .
16.(2022·安徽合肥庐阳区期末)如图,矩形纸片ABCD中,AB=4,AD=6,点G是边AD上的点,AG=2,点H是边BC上一点,连接GH,将纸片沿GH折叠,A,B的对应点分别为E,F.
(1)当点F在边DC上时,CF的长为 ;
(2)CF的最小值为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.(1) (2)
三、解答题(本大题共6小题,满分52分)
17.(6分)(2021·福建三明期末)如图,在 ABCD中,点E,F分别在边AD,BC上,且AE=CF,连接EF交AC于点O.求证:点O是线段EF的中点.
18.(6分)如图,四边形ABCD是菱形,AC与BD相交于点O,BE=AB,且A,B,E三点共线.
(1)求证:BD=EC.
(2)若∠E=50°,求∠BAO的度数.
19.(8分) (2022·河南许昌建安区期中)在数学课上,老师提出如下问题:如图,在Rt△ABC中,∠ABC=90°.求作:矩形ABCD.
小东的作法如下:
①作线段AC的垂直平分线交AC于点O;
②连接BO并延长,在延长线上截取OD=OB;
③连接AD,CD.
则四边形ABCD即为所求作的矩形.
(1)使用直尺和圆规,依据小东的作法补全图形;(保留作图痕迹)
(2)完成下边的证明.
证明:∵OA= ,OD=OB,
∴四边形ABCD是平行四边形( ).
(填依据)
∵∠ABC=90°,
∴四边形ABCD是矩形( ).(填依据)
20.(10分)(2021·山东滨州一模)如图,P是正方形ABCD对角线BD上的一点,PE⊥BC于点E,PF⊥CD于点F.
(1)求证:PA=EF.
(2)若正方形ABCD的边长为12,求四边形PFCE的周长.
21.(10分)如图(1),在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,连接P C.
(1)求∠CPE的度数;
(2)把正方形ABCD改为菱形ABCD,其他条件不变,如图(2),当∠ABC=120°时,连接CE,试探究线段AP与线段CE之间的数量关系,并说明理由.
图(1) 图(2)
22.(12分)在四边形ABCD中,对角线AC,BD相交于点O,过点O的两条直线分别交边AB,CD,AD,BC于点E,F,G,H.
(1)感知
如图(1),若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S正方形ABCD;
(2)拓展
如图(2),若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a,b,m的代数式表示);
(3)探究
如图(3),若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F,G,H的位置,使直线EF,GH把平行四边形ABCD的面积四等分.
图(1) 图(2) 图(3)
第19章 四边形
1 2 3 4 5 6 7 8 9 10
C A D B B C D D A C
11.AB=CD(答案不唯一) 12.4 13.10+2
14.80 15.()n-1 16.(1)2 (2)4-2
1.C 【关键】平行四边形的对角线互相平分
2.A ∵四边形ABCD和四边形AEFG都是矩形,∴∠FGA=90°,CD∥AB,∴∠DGA=∠BAG=20°,∴∠DGF=90°-∠DGA=90°-20°=70°.
3.D 若四边形ABCD是正方形,则四边形ABCD一定是平行四边形.
4.B ∵四边形ABCD是菱形,∠ABC=140°,∴∠ABD=∠CBD=∠ABC=70°,BO=DO.∵DE⊥BC,∴OE=OD=OB,∠BDE=20°,
∴∠OED=∠ODE=20°.
5.B ∵∠A+∠B+∠E=300°,∴∠EDC+∠BCD=(5-2)×180°-300°=240°.又DP,CP分别平分∠EDC,∠BCD,∴∠PDC+
∠PCD=120°,∴∠P=180°-(∠PDC+∠PCD)=180°-120°=60°.
6.C ∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°.∵△ADE是等边三角形,∴AD=AE,∠DAE=∠AED=60°,∴∠BAE=
150°,AB=AE,∴∠AEB=15°,∴∠BED=60°-15°=45°.
7.D (排除法)∵点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,∴EH=BD=FG,EH∥BD∥FG,∴四边形EFGH是平行四边形.由AC=BD可得EH=EF,∴四边形EFGH为菱形,A选项错误;由AC⊥BD,可得EH⊥EF,∴四边形EFGH为矩形,B选项错误.由四边形EFGH是平行四边形,无法得到AC与BD互相平分,C选项错误.故选D.
8.D 连接CD,∵DE⊥BC,DF⊥AC,∠ACB=90°,∴四边形CEDF是矩形,∴EF=CD.当CD⊥AB时,CD的长有最小值,即此时线段EF的长有最小值.∵AC=3,BC=4,∴AB==5.当CD⊥AB时,S△ABC=AB·CD=AC·BC,∴CD==,即线段EF的长的最小值为.
9.A 如图,过点D'作D'M⊥AB于点M,则∠D'MA=90°.∵四边形ABCD是正方形,∴正方形ABCD的面积=AB2.∵∠DAD'
=30°,∴∠D'AM=60°,∠AD'M=30°.在Rt△D'AM中,由勾股定理可得D'M=AD'.∵四边形ABC'D'是菱形,∴AD'=AB,即D'M=AB,∴菱形ABC'D'的面积=AB×D'M=AB2,∴菱形ABC'D'与正方形ABCD的面积之比==.
10.C 如图,当点E与点B重合时,点M位于AB的中点,点N位于BF的中点;当点E与点C重合时,点M(记为M')位于AC的中点,点N(记为N')位于FC的中点.连接MN,MM',NN',M'N'.∵M是AB的中点,M'是AC的中点,N是BF的中点,N'是FC的中点,∴MM',NN'分别是△ABC,△FBC的中位线,∴MM'∥BC且MM'=BC,NN'∥BC且NN'=BC,∴四边形MM'N'N为平行四边形,∴线段MN所扫过的区域为平行四边形.∵四边形ABCD是矩形,∴CD=AB=9.∵DF=5,∴FC=9-5=4,∴S平行四边形MM'N'N=BC·(AB-FC)=×12×(×9-×4)=15.
11.AB=CD(答案不唯一,或AD∥BC等)
12.4 ∵E,F分别是AD,BD的中点,∴AB=2EF=4.∵四边形ABCD是菱形,∴BC=AB=4.
13.10+2 ∵四边形ABCD是矩形,∴BC=AD=8,CD=AB=4,∠ABC=90°,∴AC==4.∵O是AC的中点,∴BO=AC=2.∵AO=OC,AM=MD=4,∴OM=CD=2,∴四边形ABOM的周长为AB+OB+OM+AM=
4+2+2+4=10+2.
14.80 由题意可知,小明所走的路线是正多边形,∵360°÷45°=8,∴该正多边形是正八边形,故小明所走的路程为8×10=80(米).
15.()n-1 ∵四边形ABCD为正方形,∴AB=BC=1,∠B=90°,∴AC2=AB2+BC2=12+12,∴AC=.同理可求得AE=()2,AG=()3,…,∴第n个正方形的边长为()n-1.
16.(1)2 (2)4-2 (1)由题意得CD=AB=4,如图(1),作GM⊥BC于点M,GN⊥HF于点N,连接GF,则四边形GMCD为矩形,∴GM=CD=4.由折叠可知∠GHB=∠GHF,GE=AG=2.∵GM⊥BC,GN⊥HF,∴GN=GM=4.又GD=AD-AG=6-2=4,∴GD=GN.在Rt△GDF和Rt△GNF中,∴Rt△GDF≌Rt△GNF,∴DF=NF.∵∠E=∠EFN=∠GNF=90°,∴四边形GNFE为矩形,∴NF=GE=2,∴DF=NF=2,∴CF=CD-DF=4-2=2.(2)如图(2),连接CG,GF,由勾股定理得GF=
==2.∵DG=4,∴CG==4.在△CFG中,∵CF≥CG-GF,∴CF≥4-2,∴CF的最小值为4-2.
图(1) 图(2)
17.证明:证法一 如图,连接AF,CE.
∵ABCD为平行四边形,∴AE∥FC.
又AE=CF,
∴四边形AECF是平行四边形, (4分)
∴OE=OF,∴点O是线段EF的中点. (6分)
证法二 ∵ABCD为平行四边形,
∴AD∥BC,∴∠EAO=∠FCO. (2分)
在△AOE和△COF中,
∴△AOE≌△COF,∴OE=OF, (5分)
即点O是线段EF的中点. (6分)
18.解:(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD.
又BE=AB,A,B,E三点共线,
∴BE=CD,BE∥CD, (2分)
∴四边形BECD是平行四边形,
∴BD=EC. (3分)
(2)∵四边形BECD是平行四边形,
∴BD∥CE,∴∠ABO=∠E=50°. (4分)
∵四边形ABCD是菱形,∴AC⊥BD,
∴∠BAO=90°-∠ABO=90°-50°=40°. (6分)
19.解:(1)如图,矩形ABCD即为所求.
(5分)
(2)OC (6分)
对角线互相平分的四边形是平行四边形 (7分)
有一个角是直角的平行四边形是矩形 (8分)
20.解:(1)证明:如图,连接PC.
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠BCD=90°.
在△ABP与△CBP中,
∴△ABP≌△CBP,∴PA=PC.
∵PE⊥BC,PF⊥CD,
∠BCD=90°, (4分)
∴四边形PFCE是矩形,
∴EF=PC,∴PA=EF. (5分)
(2)由(1)知四边形PFCE是矩形,
∴PE=CF,PF=CE.
∵∠CBD=45°,∠PEB=90°,
∴∠BPE=45°,∴BE=PE. (7分)
由题意可知BC=12,
∴矩形PFCE的周长=2(PE+EC)=2(BE+EC)=2BC=24. (10分)
21.解:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADP=∠CDP=45°.
又PD=PD,
∴△ADP≌△CDP,∴∠DAP=∠DCP.
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E.
∵∠CFP=∠EFD,
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPE=∠EDF=90°. (4分)
(2)AP=CE. (5分)
理由:∵四边形ABCD是菱形,∠ABC=120°,
∴AB=BC,∠ABP=∠CBP=60°.
又PB=PB,∴△ABP≌△CBP,
∴PA=PC,∠BAP=∠BCP,
∴∠DAP=∠DCP.
∵PA=PE,∴PC=PE,∠DAP=∠AEP,
∴∠DCP=∠AEP.
∵∠CFP=∠EFD,
∴180°-∠CFP-∠PCF=180°-∠EFD-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,∴AP=CE. (10分)
22.解:(1) (2分)
(2)在题图(2)中,过点O分别作ON⊥AD于点N,OM⊥AB于点M,
则OM=AD=b,ON=AB=a.
∵S△AOB=S矩形ABCD,S四边形AEOG=S矩形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,
即S△BOE=S△AOG.
∵S△BOE=BE·OM=m·b=mb,
S△AOG=AG·ON=AG·a=AG·a,
∴mb=AG·a,
∴AG=. (7分)
(3)在题图(3)中,过点O分别作OK⊥AB于点K,OQ⊥AD于点Q,并分别延长KO,QO交CD,BC于点L,P.
易得KL=2OK,PQ=2OQ.
∵S平行四边形ABCD=AB·KL=AD·PQ,
∴3×2OK=5×2OQ,
∴=.
∵S△AOB=S平行四边形ABCD,
S四边形AEOG=S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△AOB-S△AOE=S四边形AEOG-S△AOE,
∴S△BOE=S△AOG.
∵S△BOE=BE·OK=×1×OK,S△AOG=AG·OQ,
∴×1×OK=AG·OQ,
∴AG==.
易证△AOG≌△COH,△BOE≌△DOF,
∴CH=AG=,DF=BE=1.
∴当点G到点A的距离、点H到点C的距离均为,点F到点D的距离为1时,直线EF,GH把平行四边形ABCD的面积四等分. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
