第20章 数据的初步分析单元测试题(含答案)
文档属性
| 名称 | 第20章 数据的初步分析单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 17:17:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版数学八年级下学期
第20章 数据的初步分析
时间:60分钟 满分:100分
题号 一 二 三 评价
错题
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
1. (2022·广东揭阳二模)在端午节到来之前,学校食堂推荐了A,B,C三家粽子专卖店,对全校师生爱吃哪家店的粽子进行调查,以决定最终向哪家店采购.下面统计量中最值得关注的是 ( )
A. 平均数 B. 方差 C. 中位数 D. 众数
2.(2022·安徽蚌埠期末)在一次调查中,出现A种情况的频率为0.3,其余情况出现的频数之和为63,则这次调查的总数为 ( )
A. 63 B. 100 C. 90 D. 126
3.(2022·安徽合肥期末改编)已知一组数据3,3,5,6,7,8,10,那么6是这组数据的 ( )
A. 平均数但不是中位数
B. 中位数但不是平均数
C. 众数
D. 平均数也是中位数
4.(2022·河北保定期末)甲、乙、丙、丁四位同学本学期5次50米短跑成绩的平均数(s)及方差s2如表所示.要从这四位同学中选出一位用时少且发挥稳定的同学参加学校比赛,应该选( )
甲 乙 丙 丁
7 7 7.5 7.5
s2 2.1 1.9 2 1.8
A. 甲 B. 乙 C. 丙 D. 丁
5.(2022·浙江绍兴越城区期末)“红色小讲解员”演讲比赛中,7位评委分别给出某位选手的“原始分”.按照比赛规则,评定该选手的成绩时,采用“有效分”,即从7个“原始分”中去掉一个最高分和一个最低分,得到5个“有效分”,那么5个“有效分”与7个“原始分”相比,这两组数据一定不变的是 ( )
A. 中位数 B. 众数 C. 平均数 D. 方差
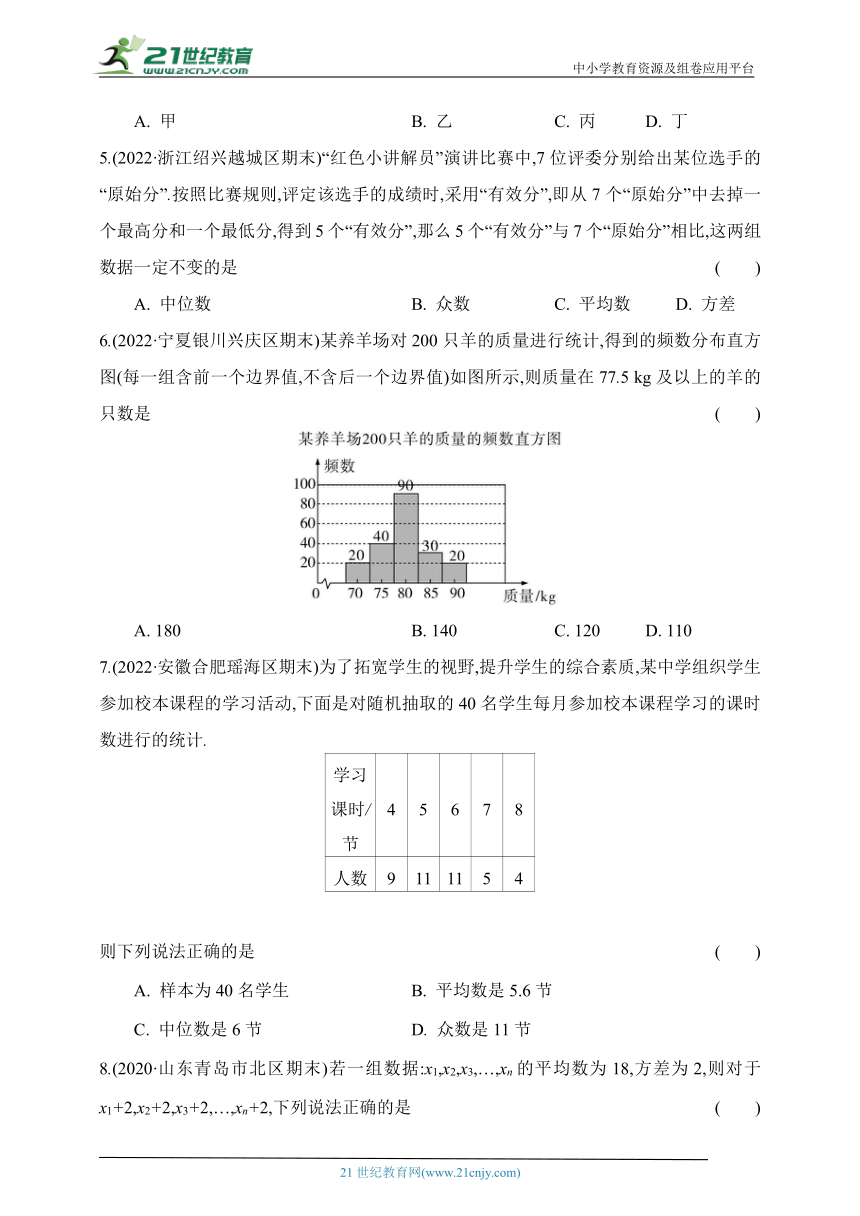
6.(2022·宁夏银川兴庆区期末)某养羊场对200只羊的质量进行统计,得到的频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,则质量在77.5 kg及以上的羊的只数是 ( )
A. 180 B. 140 C. 120 D. 110
7.(2022·安徽合肥瑶海区期末)为了拓宽学生的视野,提升学生的综合素质,某中学组织学生参加校本课程的学习活动,下面是对随机抽取的40名学生每月参加校本课程学习的课时数进行的统计.
学习课时/节 4 5 6 7 8
人数 9 11 11 5 4
则下列说法正确的是 ( )
A. 样本为40名学生 B. 平均数是5.6节
C. 中位数是6节 D. 众数是11节
8.(2020·山东青岛市北区期末)若一组数据:x1,x2,x3,…,xn的平均数为18,方差为2,则对于x1+2,x2+2,x3+2,…,xn+2,下列说法正确的是 ( )
A. 平均数为20,方差为2
B. 平均数为20,方差为4
C. 平均数为18,方差为2
D. 平均数为18,方差为4
9.(2021·广西崇左江州区期末改编)某单位招录考试的成绩的计算方法是:综合成绩=笔试成绩×60%+面试成绩×40%.某次招录考试中(成绩均为整数分数),小明的笔试成绩是82分,小芳的笔试成绩是85分,若小明的综合成绩要超过小芳,则小明的面试成绩至少比小芳多 ( )
A. 6分 B. 5分 C. 4分 D. 3分
10.(2022·安徽芜湖期末)疫情期间,某市实行静态管理,九年级某班组建了若干个数学学习互助小组,其中一个9人小组进行数学线上学习效果的自测,九名学生的平均成绩为73分.若将他们的成绩从高分到低分排序后,前五名学生的平均成绩为85分,后五名学生的平均成绩为63分,则这九名学生成绩的中位数是 ( )
A. 84分 B. 83分 C. 74分 D. 73分
二、填空题(本大题共5小题,每小题4分,满分20分)
11.参加演讲比赛前,小林和小明在班级中进行赛前训练的10次成绩如图所示,根据图中的信息,他们成绩的方差的大小关系是 .(填“>”“<”或“=”)
12.(2021·浙江宁波镇海区期末)统计得到的一组数据有80个,其中最大值为139,最小值为50,取组距为10,可分成 组.
13.(2022·河北邯郸永年区期末)小明在计算一组数据的方差时,列出的算式如下:s2=[2(7-)2+3(8-)2+(9-)2],根据算式信息,这组数据的众数是 .
14.小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表.
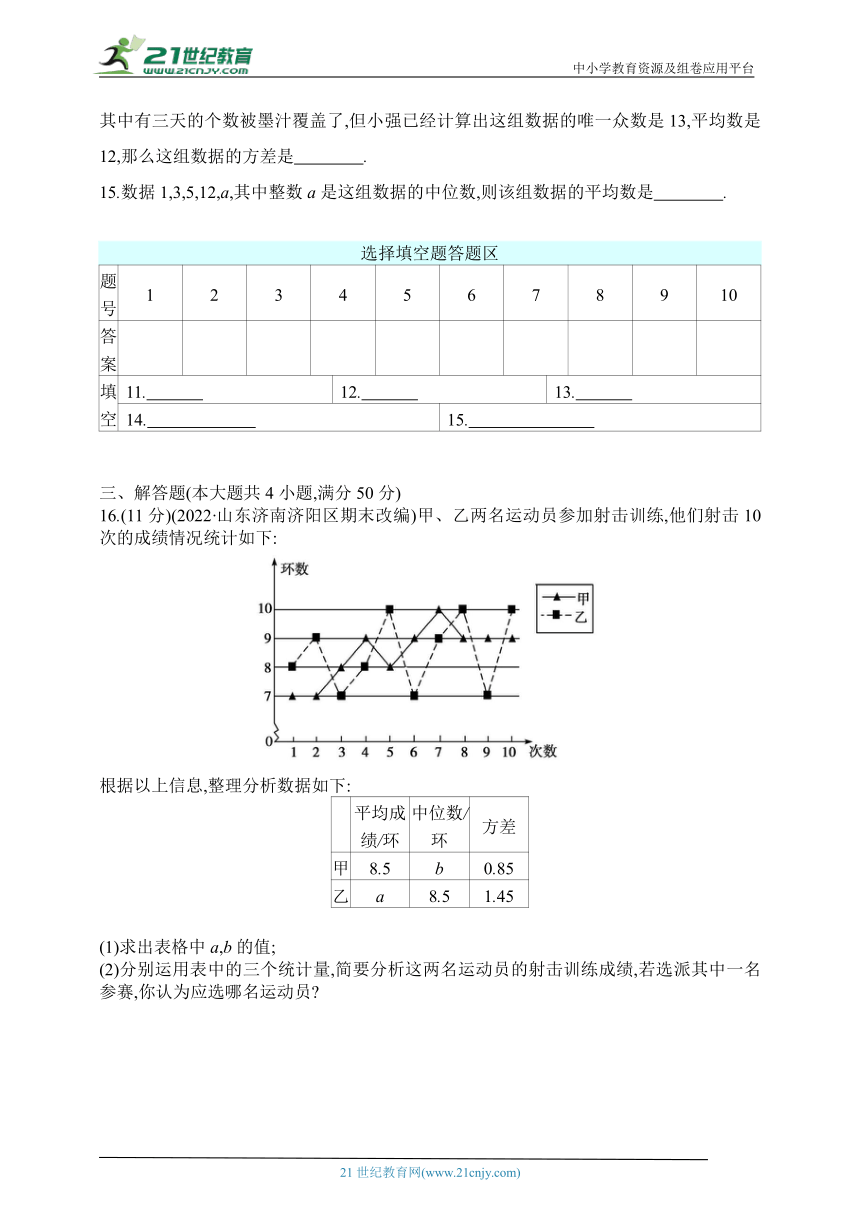
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据的唯一众数是13,平均数是12,那么这组数据的方差是 .
15.数据1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(本大题共4小题,满分50分)
16.(11分)(2022·山东济南济阳区期末改编)甲、乙两名运动员参加射击训练,他们射击10次的成绩情况统计如下:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 方差
甲 8.5 b 0.85
乙 a 8.5 1.45
(1)求出表格中a,b的值;
(2)分别运用表中的三个统计量,简要分析这两名运动员的射击训练成绩,若选派其中一名参赛,你认为应选哪名运动员
17.(12分)(2021 ·湖南长沙雨花区期末)某学校开展了防疫知识的宣传教育活动,为了解这次活动的效果,学校从全校1 500名学生中随机抽取部分学生进行测试(测试满分100分、得分均为不小于60的整数),测试成绩分为四个等级.基本合格:60≤x<70,合格:70≤x<80,良好:80≤x<90,优秀:90≤x≤100.绘制出如下统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)本次测试抽取的学生人数有 名,补全频数直方图.
(2)这次测试成绩的中位数所属的等级是 .
(3)如果全校学生都参加测试,请你估计该校获得优秀的学生人数.
18.(13分)2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
a. 成绩频数分布表:
成绩 x/分 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
频数 7 9 12 16 6
b. 成绩在70≤x<80这一组的是(单位:分):
70 71 72 72 74 77 78 78 78 7979 79
根据以上信息,回答下列问题.
(1)在这次测试中,成绩的中位数是 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗 请说明理由.
(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.
19.(14分)为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了A市20户居民全年月平均用电量(单位:kW·h),数据如下:
155,198,175,158,158,124,154,148,169,120,
190,133,160,215,172,126,145,130,131,118.
得到如下频数分布表:
全年月平均用电量/(kW·h) 频数 频率
100≤x<120 1 5%
120≤x<140
140≤x<160
160≤x<180 4
180≤x<200 2
200≤x<220 1
合计 20 100%
得到频数直方图,如下:
(1)补全频数分布表和频数直方图;
(2)若根据频数分布表制成扇形统计图,则不低于160 kW·h的部分所对应的圆心角的度数为 ;
(3)若A市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗 请说明理由.
档次 全年月平均用 电量/(kW·h) 电价/[元/ (kW·h)]
第一档 0~180 0.52
第二档 181~280 0.55
第三档 280以上 0.82
第20章 数据的初步分析
1 2 3 4 5 6 7 8 9 10
D C D B A B B A B B
11.< 12.9 13.8
14. 15.4.8,5或5.2
1.D
2.C 63÷(1-0.3)=90.
3.D 4.B 5.A
6.B 90+30+20=140(只).
7.B 样本为40名学生每月参加校本课程学习的课时数;平均数==5.6(节);中位数==5.5(节);众数是5节和6节.
8.A 【点拨】若一组数据x1,x2,…,xn的平均数为,方差为s2,则数据mx1+b,mx2+b,…,mxn+b的平均数为m+b,方差为m2s2
9.B 解法一 设小明的面试成绩为x分,小芳的面试成绩为y分,则82×60%+40%x>85×60%+40%y,∴0.4x-0.4y>(85-82)×0.6,∴x-y>4.5,即小明的面试成绩至少比小芳多5分.
解法二 由题意知,小明的笔试成绩比小芳少3分,∵笔试成绩占60%,面试成绩占40%,∴3×60%=1.8(分),1.8÷40%=
4.5(分),即小明面试成绩至少要比小芳多5分.
10.B 由题意可得,这九名学生成绩的中位数是第五名学生的成绩,第五名学生的成绩为85×5-(73×9-63×5)=83(分),故选B.
11.< 由题图可以看出,小林的成绩波动较大,根据方差的意义知,数据波动越大,则方差越大,故<.
12.9
13.8 ∵在这6个数中,8出现了3次,出现的次数最多,∴这组数据的众数是8.
14. ∵平均数是12,∴这组数据的和为12×7=84,∴被墨汁覆盖的三天的个数的和为84-(11+12+13+12)=36.∵这组数据唯一众数是13,∴被墨汁覆盖的三个数为10,13,13,∴s2=[(11-12)2+(12-12)2+(10-12)2+(13-12)2+(13-12)2+(13-12)2+(12-12)2]=.
15.4.8,5或5.2 (分类讨论思想)∵数据1,3,5,12,a的中位数是整数a,∴a=3或a=4或a=5.当a=3时,这组数据的平均数为=4.8;当a=4时,这组数据的平均数为=5;当a=5时,这组数据的平均数为=5.2.故该组数据的平均数是4.8,5或5.2.
16.解:(1)乙的平均成绩a=(8+9+7+8+10+7+9+10+7+10)÷10=8.5,
将甲的射击成绩按从小到大的顺序排列为7,7,8,8,9,9,9,9,9,10,所以甲的射击成绩的中位数b=(9+9)÷2=9.
故a=8.5,b=9. (6分)
(2)从平均成绩看,甲、乙两人的平均成绩相等,均为8.5环.从中位数看,甲的中位数大于乙的中位数.从方差看,甲的成绩比乙的成绩稳定. (9分)
综合以上因素,若选派一名运动员参加比赛,应选甲参赛.(答案合理即可) (11分)
17.解:(1)200 (2分)
补全频数直方图如图. (4分)
(2)良好 (7分)
(3)×1 500=300(人).
答:估计该校获得优秀的学生有300人. (12分)
18.解:(1)78.5 44% (4分)
(2)不正确.
理由:因为甲的成绩77分低于中位数78.5分,所以甲的成绩不可能高于一半学生的成绩. (9分)
(3)测试成绩不低于80分的人数占测试人数的44%,说明该校学生对“航空航天知识”的掌握情况较好.(答案不唯一,合理即可) (13分)
19.解:(1)补全的频数分布表: (3分)
全年月平均用电量/(kW·h) 频数 频率
100≤x<120 1 5%
120≤x<140 6 30%
140≤x<160 6 30%
160≤x<180 4 20%
180≤x<200 2 10%
200≤x<220 1 5%
合计 20 100%
补全的频数直方图: (8分)
(2)126° (11分)
解法提示:360°×(20%+10%+5%)=126°.
(3)合理. (12分)
理由:从统计图表中可以看出A市居民全年月平均用电量小于180 kW·h的占85%,即第一档全年月平均用电量覆盖了大多数的居民家庭,因此该方案是合理的. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版数学八年级下学期
第20章 数据的初步分析
时间:60分钟 满分:100分
题号 一 二 三 评价
错题
一、选择题(本大题共10小题,每小题3分,满分30分.每小题有四个选项,其中只有一个选项符合题意)
1. (2022·广东揭阳二模)在端午节到来之前,学校食堂推荐了A,B,C三家粽子专卖店,对全校师生爱吃哪家店的粽子进行调查,以决定最终向哪家店采购.下面统计量中最值得关注的是 ( )
A. 平均数 B. 方差 C. 中位数 D. 众数
2.(2022·安徽蚌埠期末)在一次调查中,出现A种情况的频率为0.3,其余情况出现的频数之和为63,则这次调查的总数为 ( )
A. 63 B. 100 C. 90 D. 126
3.(2022·安徽合肥期末改编)已知一组数据3,3,5,6,7,8,10,那么6是这组数据的 ( )
A. 平均数但不是中位数
B. 中位数但不是平均数
C. 众数
D. 平均数也是中位数
4.(2022·河北保定期末)甲、乙、丙、丁四位同学本学期5次50米短跑成绩的平均数(s)及方差s2如表所示.要从这四位同学中选出一位用时少且发挥稳定的同学参加学校比赛,应该选( )
甲 乙 丙 丁
7 7 7.5 7.5
s2 2.1 1.9 2 1.8
A. 甲 B. 乙 C. 丙 D. 丁
5.(2022·浙江绍兴越城区期末)“红色小讲解员”演讲比赛中,7位评委分别给出某位选手的“原始分”.按照比赛规则,评定该选手的成绩时,采用“有效分”,即从7个“原始分”中去掉一个最高分和一个最低分,得到5个“有效分”,那么5个“有效分”与7个“原始分”相比,这两组数据一定不变的是 ( )
A. 中位数 B. 众数 C. 平均数 D. 方差
6.(2022·宁夏银川兴庆区期末)某养羊场对200只羊的质量进行统计,得到的频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,则质量在77.5 kg及以上的羊的只数是 ( )
A. 180 B. 140 C. 120 D. 110
7.(2022·安徽合肥瑶海区期末)为了拓宽学生的视野,提升学生的综合素质,某中学组织学生参加校本课程的学习活动,下面是对随机抽取的40名学生每月参加校本课程学习的课时数进行的统计.
学习课时/节 4 5 6 7 8
人数 9 11 11 5 4
则下列说法正确的是 ( )
A. 样本为40名学生 B. 平均数是5.6节
C. 中位数是6节 D. 众数是11节
8.(2020·山东青岛市北区期末)若一组数据:x1,x2,x3,…,xn的平均数为18,方差为2,则对于x1+2,x2+2,x3+2,…,xn+2,下列说法正确的是 ( )
A. 平均数为20,方差为2
B. 平均数为20,方差为4
C. 平均数为18,方差为2
D. 平均数为18,方差为4
9.(2021·广西崇左江州区期末改编)某单位招录考试的成绩的计算方法是:综合成绩=笔试成绩×60%+面试成绩×40%.某次招录考试中(成绩均为整数分数),小明的笔试成绩是82分,小芳的笔试成绩是85分,若小明的综合成绩要超过小芳,则小明的面试成绩至少比小芳多 ( )
A. 6分 B. 5分 C. 4分 D. 3分
10.(2022·安徽芜湖期末)疫情期间,某市实行静态管理,九年级某班组建了若干个数学学习互助小组,其中一个9人小组进行数学线上学习效果的自测,九名学生的平均成绩为73分.若将他们的成绩从高分到低分排序后,前五名学生的平均成绩为85分,后五名学生的平均成绩为63分,则这九名学生成绩的中位数是 ( )
A. 84分 B. 83分 C. 74分 D. 73分
二、填空题(本大题共5小题,每小题4分,满分20分)
11.参加演讲比赛前,小林和小明在班级中进行赛前训练的10次成绩如图所示,根据图中的信息,他们成绩的方差的大小关系是 .(填“>”“<”或“=”)
12.(2021·浙江宁波镇海区期末)统计得到的一组数据有80个,其中最大值为139,最小值为50,取组距为10,可分成 组.
13.(2022·河北邯郸永年区期末)小明在计算一组数据的方差时,列出的算式如下:s2=[2(7-)2+3(8-)2+(9-)2],根据算式信息,这组数据的众数是 .
14.小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表.
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据的唯一众数是13,平均数是12,那么这组数据的方差是 .
15.数据1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(本大题共4小题,满分50分)
16.(11分)(2022·山东济南济阳区期末改编)甲、乙两名运动员参加射击训练,他们射击10次的成绩情况统计如下:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 方差
甲 8.5 b 0.85
乙 a 8.5 1.45
(1)求出表格中a,b的值;
(2)分别运用表中的三个统计量,简要分析这两名运动员的射击训练成绩,若选派其中一名参赛,你认为应选哪名运动员
17.(12分)(2021 ·湖南长沙雨花区期末)某学校开展了防疫知识的宣传教育活动,为了解这次活动的效果,学校从全校1 500名学生中随机抽取部分学生进行测试(测试满分100分、得分均为不小于60的整数),测试成绩分为四个等级.基本合格:60≤x<70,合格:70≤x<80,良好:80≤x<90,优秀:90≤x≤100.绘制出如下统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)本次测试抽取的学生人数有 名,补全频数直方图.
(2)这次测试成绩的中位数所属的等级是 .
(3)如果全校学生都参加测试,请你估计该校获得优秀的学生人数.
18.(13分)2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
a. 成绩频数分布表:
成绩 x/分 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x≤100
频数 7 9 12 16 6
b. 成绩在70≤x<80这一组的是(单位:分):
70 71 72 72 74 77 78 78 78 7979 79
根据以上信息,回答下列问题.
(1)在这次测试中,成绩的中位数是 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗 请说明理由.
(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.
19.(14分)为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了A市20户居民全年月平均用电量(单位:kW·h),数据如下:
155,198,175,158,158,124,154,148,169,120,
190,133,160,215,172,126,145,130,131,118.
得到如下频数分布表:
全年月平均用电量/(kW·h) 频数 频率
100≤x<120 1 5%
120≤x<140
140≤x<160
160≤x<180 4
180≤x<200 2
200≤x<220 1
合计 20 100%
得到频数直方图,如下:
(1)补全频数分布表和频数直方图;
(2)若根据频数分布表制成扇形统计图,则不低于160 kW·h的部分所对应的圆心角的度数为 ;
(3)若A市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗 请说明理由.
档次 全年月平均用 电量/(kW·h) 电价/[元/ (kW·h)]
第一档 0~180 0.52
第二档 181~280 0.55
第三档 280以上 0.82
第20章 数据的初步分析
1 2 3 4 5 6 7 8 9 10
D C D B A B B A B B
11.< 12.9 13.8
14. 15.4.8,5或5.2
1.D
2.C 63÷(1-0.3)=90.
3.D 4.B 5.A
6.B 90+30+20=140(只).
7.B 样本为40名学生每月参加校本课程学习的课时数;平均数==5.6(节);中位数==5.5(节);众数是5节和6节.
8.A 【点拨】若一组数据x1,x2,…,xn的平均数为,方差为s2,则数据mx1+b,mx2+b,…,mxn+b的平均数为m+b,方差为m2s2
9.B 解法一 设小明的面试成绩为x分,小芳的面试成绩为y分,则82×60%+40%x>85×60%+40%y,∴0.4x-0.4y>(85-82)×0.6,∴x-y>4.5,即小明的面试成绩至少比小芳多5分.
解法二 由题意知,小明的笔试成绩比小芳少3分,∵笔试成绩占60%,面试成绩占40%,∴3×60%=1.8(分),1.8÷40%=
4.5(分),即小明面试成绩至少要比小芳多5分.
10.B 由题意可得,这九名学生成绩的中位数是第五名学生的成绩,第五名学生的成绩为85×5-(73×9-63×5)=83(分),故选B.
11.< 由题图可以看出,小林的成绩波动较大,根据方差的意义知,数据波动越大,则方差越大,故<.
12.9
13.8 ∵在这6个数中,8出现了3次,出现的次数最多,∴这组数据的众数是8.
14. ∵平均数是12,∴这组数据的和为12×7=84,∴被墨汁覆盖的三天的个数的和为84-(11+12+13+12)=36.∵这组数据唯一众数是13,∴被墨汁覆盖的三个数为10,13,13,∴s2=[(11-12)2+(12-12)2+(10-12)2+(13-12)2+(13-12)2+(13-12)2+(12-12)2]=.
15.4.8,5或5.2 (分类讨论思想)∵数据1,3,5,12,a的中位数是整数a,∴a=3或a=4或a=5.当a=3时,这组数据的平均数为=4.8;当a=4时,这组数据的平均数为=5;当a=5时,这组数据的平均数为=5.2.故该组数据的平均数是4.8,5或5.2.
16.解:(1)乙的平均成绩a=(8+9+7+8+10+7+9+10+7+10)÷10=8.5,
将甲的射击成绩按从小到大的顺序排列为7,7,8,8,9,9,9,9,9,10,所以甲的射击成绩的中位数b=(9+9)÷2=9.
故a=8.5,b=9. (6分)
(2)从平均成绩看,甲、乙两人的平均成绩相等,均为8.5环.从中位数看,甲的中位数大于乙的中位数.从方差看,甲的成绩比乙的成绩稳定. (9分)
综合以上因素,若选派一名运动员参加比赛,应选甲参赛.(答案合理即可) (11分)
17.解:(1)200 (2分)
补全频数直方图如图. (4分)
(2)良好 (7分)
(3)×1 500=300(人).
答:估计该校获得优秀的学生有300人. (12分)
18.解:(1)78.5 44% (4分)
(2)不正确.
理由:因为甲的成绩77分低于中位数78.5分,所以甲的成绩不可能高于一半学生的成绩. (9分)
(3)测试成绩不低于80分的人数占测试人数的44%,说明该校学生对“航空航天知识”的掌握情况较好.(答案不唯一,合理即可) (13分)
19.解:(1)补全的频数分布表: (3分)
全年月平均用电量/(kW·h) 频数 频率
100≤x<120 1 5%
120≤x<140 6 30%
140≤x<160 6 30%
160≤x<180 4 20%
180≤x<200 2 10%
200≤x<220 1 5%
合计 20 100%
补全的频数直方图: (8分)
(2)126° (11分)
解法提示:360°×(20%+10%+5%)=126°.
(3)合理. (12分)
理由:从统计图表中可以看出A市居民全年月平均用电量小于180 kW·h的占85%,即第一档全年月平均用电量覆盖了大多数的居民家庭,因此该方案是合理的. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
