人教版六年级上册《圆的周长》课件(共29张PPT)
文档属性
| 名称 | 人教版六年级上册《圆的周长》课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 19:21:06 | ||
图片预览





文档简介
(共29张PPT)
科 目:数学 年 级:人教版六年级上册
圆的周长
1.结合实例,认识圆的周长。在探索测量圆的周长的方法中,体会化曲为直的思想。
2.通过实践操作理解圆周率的意义,理解和掌握圆周长的计算公式。
3.在解决与圆的周长相应的实际问题中,体会数学与生活的联系。
学习目标
线绳、直尺、实验报告单、直径是3厘米、5厘米、10厘米的三个圆形硬纸板、练习本、笔。
学具准备
回忆:
我们学的平面图形,它们周长指的是什么?
平面上封闭图形一周的长度,就是它的周长。
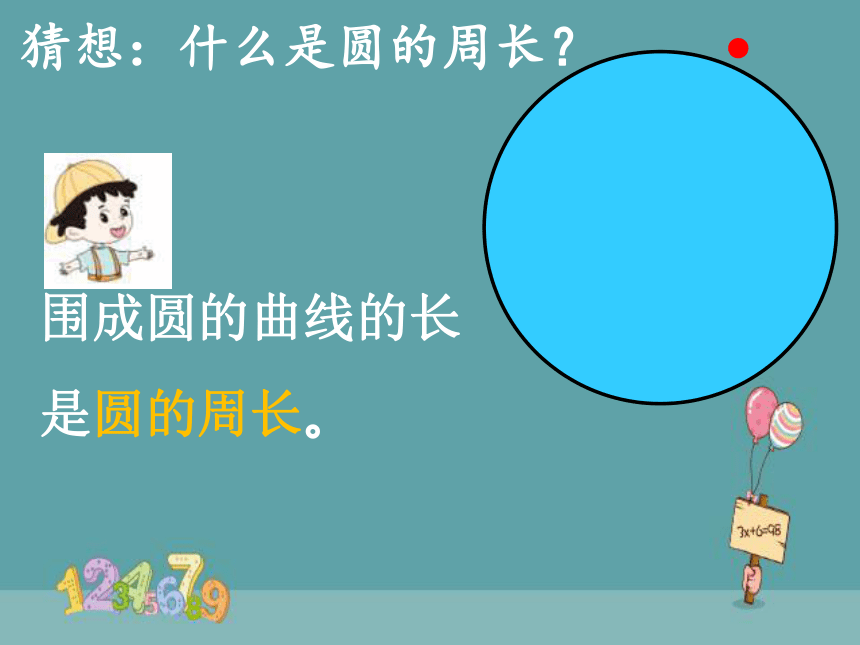
猜想:什么是圆的周长?
围成圆的曲线的长
是圆的周长。
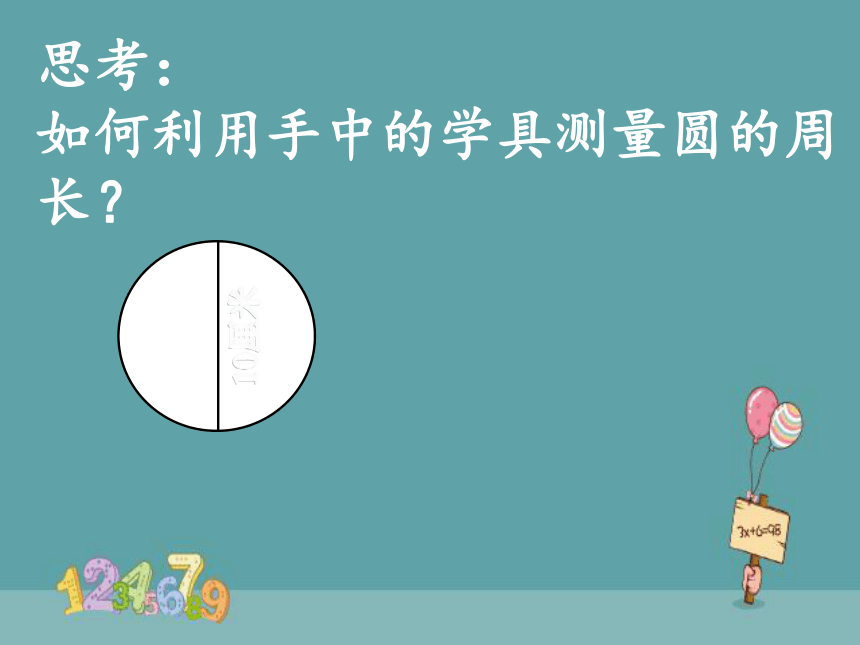
思考:
如何利用手中的学具测量圆的周长?
10厘米
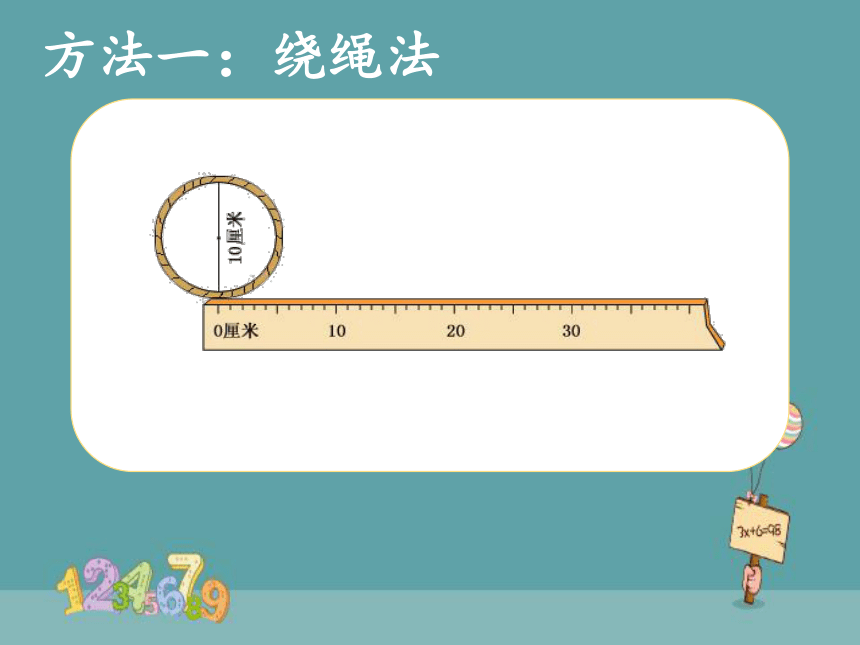
方法一:绕绳法
0cm
10
20
30
40
10厘米
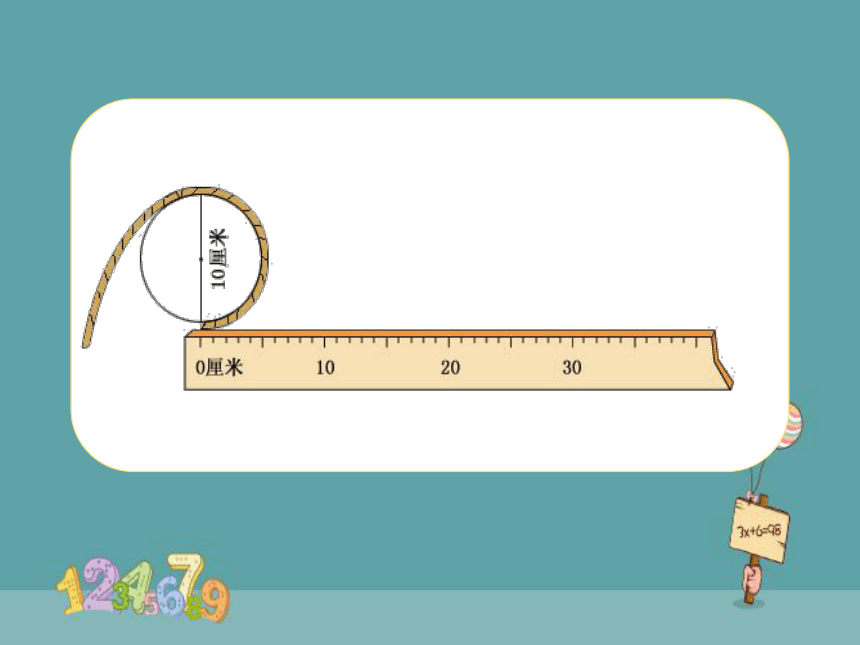
方法二:滚动法
方法一:先绕再量
方法二:滚动测量
化曲为直
思考:
如果想知道一个很大的圆的周长,该怎么办呢?
猜想:
圆周长的大小与谁有关呢?
直径?
半径?
小组合作要求:
1.小组同学在小组长的带领下,选择合适的测量方法,量出圆的周长和直径(多次测量取平均值),并填写在报告单上。
2.计算出周长与直径的比值,保留两位小数,再填写报告单。
3.观察报告单,再想一想议一议,圆的周长和直径有什么关系?
圆1
圆3
圆2
项目 周长(cm) 直径(cm) (保留两位小数)
圆1
圆2
圆3
π≈3.14
圆的周长与它的直径的比值是一个固定的数。我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数。π=3.141592653……
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早1000年。
祖冲之
圆的周长公式
圆的周长
=
直径
×
3.14
π
C
d
×
π
=
2
π
C
=
r
圆的周长÷直径 =
圆周率
1. 一个圆形喷水池的半径是5米,它的周长是多少米?
练习
2. 汽车轮胎的半径是0.3米,它滚动1圈前进多少米?滚动1000圈前进多少米?
通过今天的学习,你有什么收获吗?
大胆猜想
动手实验
解决问题
圆的周长
化曲为直
实践应用
抽象概括
课堂小结
1.完成数学课本上相对应的习题。
2.尝试测量并计算生活中某一圆形物体的周长吧!
课外作业
谢谢!
科 目:数学 年 级:人教版六年级上册
圆的周长
1.结合实例,认识圆的周长。在探索测量圆的周长的方法中,体会化曲为直的思想。
2.通过实践操作理解圆周率的意义,理解和掌握圆周长的计算公式。
3.在解决与圆的周长相应的实际问题中,体会数学与生活的联系。
学习目标
线绳、直尺、实验报告单、直径是3厘米、5厘米、10厘米的三个圆形硬纸板、练习本、笔。
学具准备
回忆:
我们学的平面图形,它们周长指的是什么?
平面上封闭图形一周的长度,就是它的周长。
猜想:什么是圆的周长?
围成圆的曲线的长
是圆的周长。
思考:
如何利用手中的学具测量圆的周长?
10厘米
方法一:绕绳法
0cm
10
20
30
40
10厘米
方法二:滚动法
方法一:先绕再量
方法二:滚动测量
化曲为直
思考:
如果想知道一个很大的圆的周长,该怎么办呢?
猜想:
圆周长的大小与谁有关呢?
直径?
半径?
小组合作要求:
1.小组同学在小组长的带领下,选择合适的测量方法,量出圆的周长和直径(多次测量取平均值),并填写在报告单上。
2.计算出周长与直径的比值,保留两位小数,再填写报告单。
3.观察报告单,再想一想议一议,圆的周长和直径有什么关系?
圆1
圆3
圆2
项目 周长(cm) 直径(cm) (保留两位小数)
圆1
圆2
圆3
π≈3.14
圆的周长与它的直径的比值是一个固定的数。我们把它叫做圆周率,用字母π表示。它是一个无限不循环小数。π=3.141592653……
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早1000年。
祖冲之
圆的周长公式
圆的周长
=
直径
×
3.14
π
C
d
×
π
=
2
π
C
=
r
圆的周长÷直径 =
圆周率
1. 一个圆形喷水池的半径是5米,它的周长是多少米?
练习
2. 汽车轮胎的半径是0.3米,它滚动1圈前进多少米?滚动1000圈前进多少米?
通过今天的学习,你有什么收获吗?
大胆猜想
动手实验
解决问题
圆的周长
化曲为直
实践应用
抽象概括
课堂小结
1.完成数学课本上相对应的习题。
2.尝试测量并计算生活中某一圆形物体的周长吧!
课外作业
谢谢!
