2014-2015学年高中人教A版数学选修2-2同步课件 3.1.1 数系的扩充和复数的概念
文档属性
| 名称 | 2014-2015学年高中人教A版数学选修2-2同步课件 3.1.1 数系的扩充和复数的概念 |  | |
| 格式 | zip | ||
| 文件大小 | 591.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-02 20:31:28 | ||
图片预览






文档简介
课件18张PPT。数系的扩充和复数的概念解方程x2+1=0在实数集中无解!印度数学家婆什迦罗(Bhaskara Ⅱ,1114-约1185)
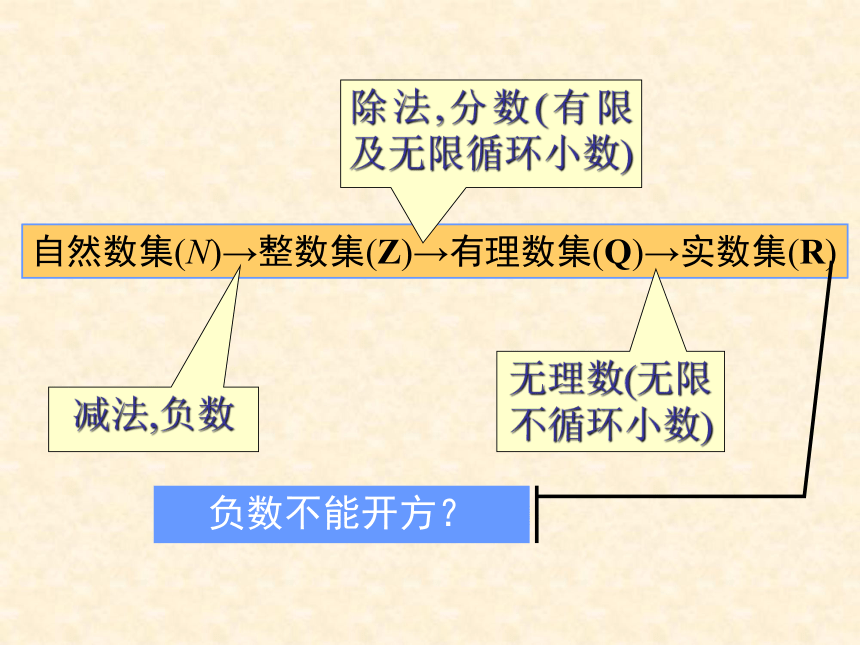
第一个遇到“x2+1=0”的人,当时他认为无意义.1484年,法国数学家舒开遇到解二次方程4+x2=3x的问题.1545年意大利数学家、怪杰卡尔丹(G.Cardan0,1501-1576)遇到方程 x2-10x+40=0自然数集(N)→整数集(Z)→有理数集(Q)→实数集(R)减法,负数除法,分数(有限及无限循环小数)无理数(无限不循环小数)负数不能开方?韦达(Fran?ois Viète; 1540 ? 1603)棣莫弗(Abraham de Moivre; 1667 ? 1754)欧拉( Leonard Euler, 1707 - 1783 )笛卡儿( René Descartes; 1596 ? 1650 )复数的概念1、为了解决负数开方问题,引入新数 i ,使i是方程 x2+1=0 的解, 即 i?i = -1把i添加到实数集中得到一个新数集,记作Ax2+1=0在A中的解为 x=i 引入的数 i 和实数之间能实现加法,乘法运算,并且加法和乘法都满足交换律,结合律,以及乘法对加法满足分配律.将实数a和数i相加记为: a+i;
把实数b与数i相乘记作: bi;
将它们的和记作: a+bi (a,b∈R),
将这些数加入数集A
得到一个新的数集: C={a+bi|a,b∈R}复数全体所组成的集合叫复数集,用字母C表示复数(complex numbers):2、复数:复数集(set of complex numbers):把形如 a+bi (a,b∈R)的数叫复数i 叫做 虚数单位(imaginary unit)用z表示复数, 即z = a + bi (a,b∈R) 叫做复数的代数形式 (algebraic form of complex)3、复数的代数形式:规定: 0i=0,0+bi=bi4、两个复数相等有两个复数z1=a+bi (a,b?R)和z2=c+di(c,d?R) 注意1、若z1,z2均为实数,则z1,z2具有大小关系2、若z1,z2中不都为实数,z1与z2只有相等或不相等两关系,而不能比较大小5、复数的分类:虚数b≠0纯虚数a=0且b≠0实数0a=b=0实数b=0例.说明下列数是否是虚数,并说明各数的实部与虚部复数集,实数集,虚数集,纯虚数集之间关系有下列命题:
(1)若a、b为实数,则 z=a+bi 为虚数
(2)若b为实数,则 z=bi 必为纯虚数
(3)若a为实数,则 z= a 一定不是虚数
其中真命题的个数为( )
(A)0 (B)1 (C)2 (D)3B例1 实数m取什么值时,复数z=m+1+(m-1)i是
(1)实数; (2)虚数; (3)纯虚数.解: (1)当m-1=0,即 m=1时,复数z 是实数.(2)当m-1≠0,即m≠1时,复数z 是虚数.(3)当m+1=0,且m-1≠0,即m=-1时,复数z 是纯虚数.关键:m的取值1. 当m为何实数时,复数 Z=m2+m-2+(m2-1)i 是
(1)实数; (2)虚数; (3)纯虚数 ; (4) 0. 2. 对上题练习中的虚数z,若实部是虚部的两倍,求实数m的值.练习4. (m2-m)+(m3-2m2-m+2)i是纯虚数,求m的值.5.m取什么实数值时,复数 z=(m2-2m-3)+(m2-4m+3)i 是实数,是虚数,是纯虚数?m=0作业:课本第104页练习3
第16页习题3.1A组1,2
第一个遇到“x2+1=0”的人,当时他认为无意义.1484年,法国数学家舒开遇到解二次方程4+x2=3x的问题.1545年意大利数学家、怪杰卡尔丹(G.Cardan0,1501-1576)遇到方程 x2-10x+40=0自然数集(N)→整数集(Z)→有理数集(Q)→实数集(R)减法,负数除法,分数(有限及无限循环小数)无理数(无限不循环小数)负数不能开方?韦达(Fran?ois Viète; 1540 ? 1603)棣莫弗(Abraham de Moivre; 1667 ? 1754)欧拉( Leonard Euler, 1707 - 1783 )笛卡儿( René Descartes; 1596 ? 1650 )复数的概念1、为了解决负数开方问题,引入新数 i ,使i是方程 x2+1=0 的解, 即 i?i = -1把i添加到实数集中得到一个新数集,记作Ax2+1=0在A中的解为 x=i 引入的数 i 和实数之间能实现加法,乘法运算,并且加法和乘法都满足交换律,结合律,以及乘法对加法满足分配律.将实数a和数i相加记为: a+i;
把实数b与数i相乘记作: bi;
将它们的和记作: a+bi (a,b∈R),
将这些数加入数集A
得到一个新的数集: C={a+bi|a,b∈R}复数全体所组成的集合叫复数集,用字母C表示复数(complex numbers):2、复数:复数集(set of complex numbers):把形如 a+bi (a,b∈R)的数叫复数i 叫做 虚数单位(imaginary unit)用z表示复数, 即z = a + bi (a,b∈R) 叫做复数的代数形式 (algebraic form of complex)3、复数的代数形式:规定: 0i=0,0+bi=bi4、两个复数相等有两个复数z1=a+bi (a,b?R)和z2=c+di(c,d?R) 注意1、若z1,z2均为实数,则z1,z2具有大小关系2、若z1,z2中不都为实数,z1与z2只有相等或不相等两关系,而不能比较大小5、复数的分类:虚数b≠0纯虚数a=0且b≠0实数0a=b=0实数b=0例.说明下列数是否是虚数,并说明各数的实部与虚部复数集,实数集,虚数集,纯虚数集之间关系有下列命题:
(1)若a、b为实数,则 z=a+bi 为虚数
(2)若b为实数,则 z=bi 必为纯虚数
(3)若a为实数,则 z= a 一定不是虚数
其中真命题的个数为( )
(A)0 (B)1 (C)2 (D)3B例1 实数m取什么值时,复数z=m+1+(m-1)i是
(1)实数; (2)虚数; (3)纯虚数.解: (1)当m-1=0,即 m=1时,复数z 是实数.(2)当m-1≠0,即m≠1时,复数z 是虚数.(3)当m+1=0,且m-1≠0,即m=-1时,复数z 是纯虚数.关键:m的取值1. 当m为何实数时,复数 Z=m2+m-2+(m2-1)i 是
(1)实数; (2)虚数; (3)纯虚数 ; (4) 0. 2. 对上题练习中的虚数z,若实部是虚部的两倍,求实数m的值.练习4. (m2-m)+(m3-2m2-m+2)i是纯虚数,求m的值.5.m取什么实数值时,复数 z=(m2-2m-3)+(m2-4m+3)i 是实数,是虚数,是纯虚数?m=0作业:课本第104页练习3
第16页习题3.1A组1,2
