2014-2015学年高中人教A版数学选修2-2同步课件 2.3 数学归纳法1
文档属性
| 名称 | 2014-2015学年高中人教A版数学选修2-2同步课件 2.3 数学归纳法1 |  | |
| 格式 | zip | ||
| 文件大小 | 182.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-02 20:32:00 | ||
图片预览








文档简介
课件20张PPT。2.3《数学归纳法》教学目标 了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
教学重点:
了解数学归纳法的原理第一课时一、归纳法
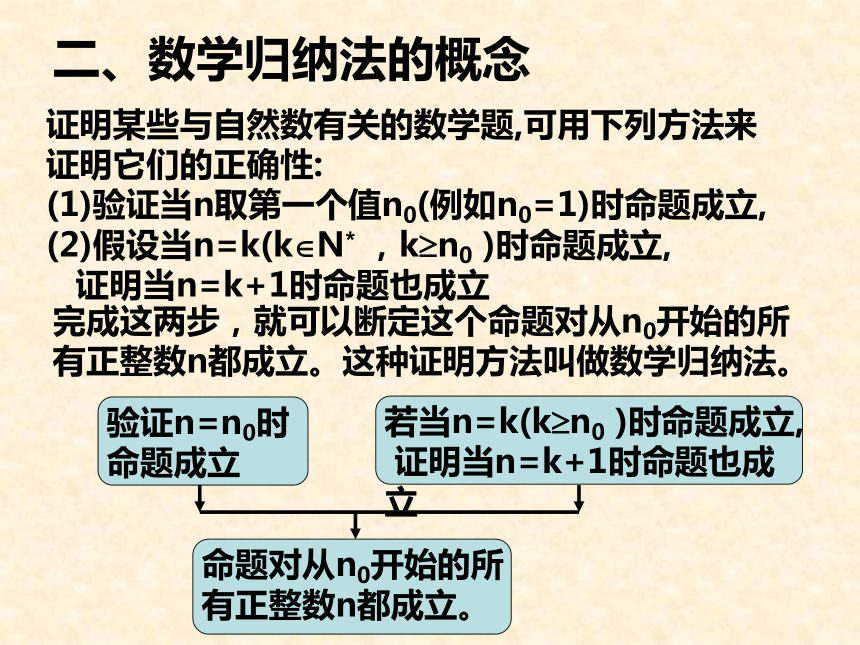
对于某类事物,由它的一些特殊事例或其全部可能情况,归纳出一般结论的推理方法,叫归纳法。特点:an=a1+(n-1)d如何证明:1+3+5+…+(2n-1)=n2 (n∈N*)二、数学归纳法的概念证明某些与自然数有关的数学题,可用下列方法来证明它们的正确性:
(1)验证当n取第一个值n0(例如n0=1)时命题成立,
(2)假设当n=k(k?N* ,k?n0 )时命题成立,
证明当n=k+1时命题也成立完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法。求证请问:
第②步中“当n=k+1时”的证明可否改换为:
1+3+5+……+(2k-1)+[2(k+1)-1]= 1+3+5+……+(2k-1)+(2k+1)
= = (k+1)2 ?为什么??例:用数学归纳法证明例、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)第二课时证明某些与自然数有关的数学题,可用下列方法来证明它们的正确性:
(1)验证当n取第一个值n0(例如n0=1)时命题成立,
(2)假设当n=k(k?N* ,k?n0 )时命题成立,
证明当n=k+1时命题也成立完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法。回顾例:已知数列
计算 ,根据计算的结果,猜想
的表达式,并用数学归纳法进行证明.例:是否存在常数a、b,使得等式:
对一切正整数n都成立,并证明你的结论.点拨:对这种类型的题目,一般先利用n的特殊值,探求出待定系数,然后用数学归纳法证明它对一切正整数n都成立.解:令n=1,2,并整理得以下用数学归纳法证明:
(2)假设当n=k时结论正确,即:
则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.(1)当n=1时,由上面解法知结论正确.例:比较 2n 与 n2 (n∈N*)的大小注:先猜想,再证明解:当n=1时,2n=2,n2=1, 2n>n2
当n=2时,2n=4,n2=4, 2n=n2
当n=3时,2n=8,n2=9, 2n 当n=4时,2n=16,n2=16, 2n=n2
当n=5时,2n=32,n2=25, 2n>n2
当n=6时,2n=64,n2=36, 2n>n2
猜想当n≥5时,2n>n2(证明略)
例:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数f(n)=n(n-1)/2.说明:用数学归纳法证明几何问题,重难点是处理好当n=k+1时利用假设结合几何知识证明命题成立.注:在上例的题设条件下还可以有如下二个结论:(1)设这n条直线互相分割成f(n)条线段或射线,
---则: f(n)=n2.(2)这n条直线把平面分成(n2+n+2)/2个区域.1:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,
证明这n条直线把平面分成f(n)=(n2+n+2)/2个区域.作业:1:n边形有f(n)条对角线,则凸n+1边形的对角线 ------的条数f(n+1)=f(n)+_________.2:设有通过一点的k个平面,其中任何三个平面或
三个以上的平面不共有一条直线,这k个平面将
空间分成f(k)个区域,则k+1个平面将空间分成
f(k+1)=f(k)+__________个区域.思考题
教学重点:
了解数学归纳法的原理第一课时一、归纳法
对于某类事物,由它的一些特殊事例或其全部可能情况,归纳出一般结论的推理方法,叫归纳法。特点:an=a1+(n-1)d如何证明:1+3+5+…+(2n-1)=n2 (n∈N*)二、数学归纳法的概念证明某些与自然数有关的数学题,可用下列方法来证明它们的正确性:
(1)验证当n取第一个值n0(例如n0=1)时命题成立,
(2)假设当n=k(k?N* ,k?n0 )时命题成立,
证明当n=k+1时命题也成立完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法。求证请问:
第②步中“当n=k+1时”的证明可否改换为:
1+3+5+……+(2k-1)+[2(k+1)-1]= 1+3+5+……+(2k-1)+(2k+1)
= = (k+1)2 ?为什么??例:用数学归纳法证明例、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)第二课时证明某些与自然数有关的数学题,可用下列方法来证明它们的正确性:
(1)验证当n取第一个值n0(例如n0=1)时命题成立,
(2)假设当n=k(k?N* ,k?n0 )时命题成立,
证明当n=k+1时命题也成立完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立。这种证明方法叫做数学归纳法。回顾例:已知数列
计算 ,根据计算的结果,猜想
的表达式,并用数学归纳法进行证明.例:是否存在常数a、b,使得等式:
对一切正整数n都成立,并证明你的结论.点拨:对这种类型的题目,一般先利用n的特殊值,探求出待定系数,然后用数学归纳法证明它对一切正整数n都成立.解:令n=1,2,并整理得以下用数学归纳法证明:
(2)假设当n=k时结论正确,即:
则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.(1)当n=1时,由上面解法知结论正确.例:比较 2n 与 n2 (n∈N*)的大小注:先猜想,再证明解:当n=1时,2n=2,n2=1, 2n>n2
当n=2时,2n=4,n2=4, 2n=n2
当n=3时,2n=8,n2=9, 2n
当n=5时,2n=32,n2=25, 2n>n2
当n=6时,2n=64,n2=36, 2n>n2
猜想当n≥5时,2n>n2(证明略)
例:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数f(n)=n(n-1)/2.说明:用数学归纳法证明几何问题,重难点是处理好当n=k+1时利用假设结合几何知识证明命题成立.注:在上例的题设条件下还可以有如下二个结论:(1)设这n条直线互相分割成f(n)条线段或射线,
---则: f(n)=n2.(2)这n条直线把平面分成(n2+n+2)/2个区域.1:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,
证明这n条直线把平面分成f(n)=(n2+n+2)/2个区域.作业:1:n边形有f(n)条对角线,则凸n+1边形的对角线 ------的条数f(n+1)=f(n)+_________.2:设有通过一点的k个平面,其中任何三个平面或
三个以上的平面不共有一条直线,这k个平面将
空间分成f(k)个区域,则k+1个平面将空间分成
f(k+1)=f(k)+__________个区域.思考题
