高二数学选修1-1 导数的概念(广东省揭阳市)
文档属性
| 名称 | 高二数学选修1-1 导数的概念(广东省揭阳市) |  | |
| 格式 | rar | ||
| 文件大小 | 521.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-31 22:42:00 | ||
图片预览








文档简介
课件20张PPT。变 化 率 问 题
与导数的概念揭东县第一中学 吴奕锋问题1.气球平均膨胀率.吹气球时,会发现:随着气球内空气容量的增加,气球的半径增加得越来越慢,能从数学的角度解释这一现象吗?解:可知:V(r)= πr3 即:r(V)= 当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球平均膨胀率: 问题1.气球平均膨胀率.当空气容量V从1加2L时,半径增加了 r(2)-r(1)= 0.16 气球平均膨胀率: 可以看出,随着气球体积变大,它的平均
膨胀率变小. 思考:当空气容量从V1增加到V2 时,气球的平均膨胀率是多少呢?问题2 高台跳水(平均速度) 在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
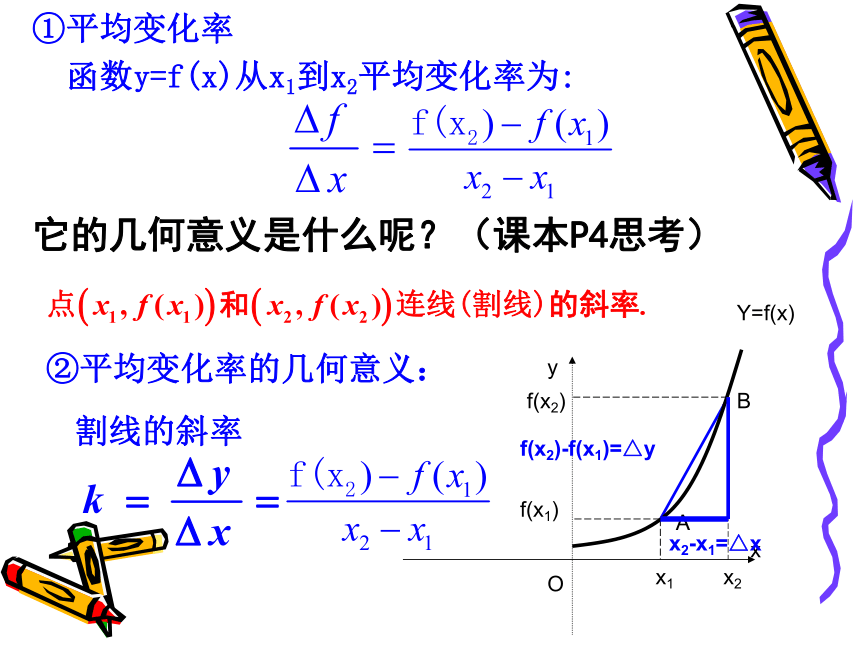
h(t)=-4.9t2+6.5t+10求1s到2s时的平均速度. 思考:求t1s到t2s时的平均速度. 平均变化率如果上述的两个函数关系用f(x)表示那么当自变量x从x1变化到x2时,函数值就从y1变化到y2则函数f(x)从x1到x2的平均变化率为:它的几何意义是什么呢?(课本P4思考)①平均变化率函数y=f(x)从x1到x2平均变化率为:②平均变化率的几何意义:
割线的斜率它的几何意义是什么呢?(课本P4思考)1.1.2 导数的概念 问题2 高台跳水 在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)
存在函数关系 h(t)=-4.9t2+6.5t+10瞬时速度.在高台跳水运动中,平均速度不能准确反映他在这段时间里运动状态.又如何求
瞬时速度呢?
我们把物体在某一时刻的速度称为瞬时速度.如何求(比如, t=2时的)瞬时速度? 通过列表看出平均速度的变化趋势?: 当Δt趋近于0时,平均速度有什么变化趋势?瞬时速度我们用
表示 “当t=2, Δt趋近于0时,平均速度趋于确定值-13.1”.那么,运动员在某一时刻t0的瞬时速度?(平均速度的极限为瞬时速度) 思考:我们利用平均速度的极限求得瞬时速度,那么如何求函数f(x)在x=x0点的瞬时变化率呢?我们称它为函数 在 处的导数,导数的定义:函数y=f(x)在x=x0处的瞬时变化率是:记做 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:问题:求函数y=3x2在x=1处的导数.
分析:先求Δy=f(1+Δx)-f(1)
=6Δx+(Δx)2再求再求应用:例1 物体作自由落体运动,运动方程为: 其中位移单位是m,时间单位是s,g=10m/s2.求:
(1) 物体在时间区间[2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t=2(s)时的瞬时速度. 分析:解:(1)将 Δt=0.1代入上式,得: (2)将 Δt=0.01代入上式,得: 应用: 例2 将原油精练为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热。如果第 x(h)时,原油的温度(单位:0C)为 f(x)=x2-7x+15(0≤x≤8).计算第2h和第6h时,原由温度的瞬时变化率,并说明它们的意义。小结:小结:1.求物体运动的瞬时速度:
(1)求位移增量
(2)求平均速度
(3)求极限2.由导数的定义可得求导数的一般步骤:
(1)求函数的增量
(2)求平均变化率
(3)求极限练习:求函数y= 在x=1处的导数.
与导数的概念揭东县第一中学 吴奕锋问题1.气球平均膨胀率.吹气球时,会发现:随着气球内空气容量的增加,气球的半径增加得越来越慢,能从数学的角度解释这一现象吗?解:可知:V(r)= πr3 即:r(V)= 当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 气球平均膨胀率: 问题1.气球平均膨胀率.当空气容量V从1加2L时,半径增加了 r(2)-r(1)= 0.16 气球平均膨胀率: 可以看出,随着气球体积变大,它的平均
膨胀率变小. 思考:当空气容量从V1增加到V2 时,气球的平均膨胀率是多少呢?问题2 高台跳水(平均速度) 在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t2+6.5t+10求1s到2s时的平均速度. 思考:求t1s到t2s时的平均速度. 平均变化率如果上述的两个函数关系用f(x)表示那么当自变量x从x1变化到x2时,函数值就从y1变化到y2则函数f(x)从x1到x2的平均变化率为:它的几何意义是什么呢?(课本P4思考)①平均变化率函数y=f(x)从x1到x2平均变化率为:②平均变化率的几何意义:
割线的斜率它的几何意义是什么呢?(课本P4思考)1.1.2 导数的概念 问题2 高台跳水 在高台跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)
存在函数关系 h(t)=-4.9t2+6.5t+10瞬时速度.在高台跳水运动中,平均速度不能准确反映他在这段时间里运动状态.又如何求
瞬时速度呢?
我们把物体在某一时刻的速度称为瞬时速度.如何求(比如, t=2时的)瞬时速度? 通过列表看出平均速度的变化趋势?: 当Δt趋近于0时,平均速度有什么变化趋势?瞬时速度我们用
表示 “当t=2, Δt趋近于0时,平均速度趋于确定值-13.1”.那么,运动员在某一时刻t0的瞬时速度?(平均速度的极限为瞬时速度) 思考:我们利用平均速度的极限求得瞬时速度,那么如何求函数f(x)在x=x0点的瞬时变化率呢?我们称它为函数 在 处的导数,导数的定义:函数y=f(x)在x=x0处的瞬时变化率是:记做 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:问题:求函数y=3x2在x=1处的导数.
分析:先求Δy=f(1+Δx)-f(1)
=6Δx+(Δx)2再求再求应用:例1 物体作自由落体运动,运动方程为: 其中位移单位是m,时间单位是s,g=10m/s2.求:
(1) 物体在时间区间[2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t=2(s)时的瞬时速度. 分析:解:(1)将 Δt=0.1代入上式,得: (2)将 Δt=0.01代入上式,得: 应用: 例2 将原油精练为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热。如果第 x(h)时,原油的温度(单位:0C)为 f(x)=x2-7x+15(0≤x≤8).计算第2h和第6h时,原由温度的瞬时变化率,并说明它们的意义。小结:小结:1.求物体运动的瞬时速度:
(1)求位移增量
(2)求平均速度
(3)求极限2.由导数的定义可得求导数的一般步骤:
(1)求函数的增量
(2)求平均变化率
(3)求极限练习:求函数y= 在x=1处的导数.
