高二数学 函数的单调性与导数(一)(广东省揭阳市)
文档属性
| 名称 | 高二数学 函数的单调性与导数(一)(广东省揭阳市) |  | |
| 格式 | rar | ||
| 文件大小 | 365.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-22 22:46:00 | ||
图片预览



文档简介
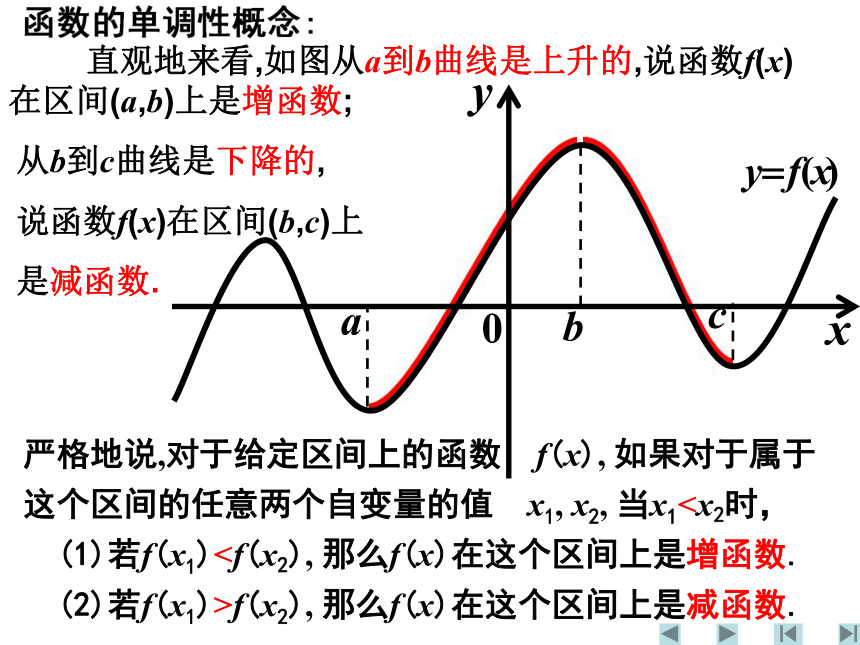
课件16张PPT。 首先我们回忆一下函数的单调性的概念和导数的几何意义.严格地说,对于给定区间上的函数 f(x), 如果对于属于这个区间的任意两个自变量的值 x1, x2, 当x1 (1)若f(x1) (2)若f(x1)>f(x2), 那么f(x)在这个区间上是减函数. 直观地来看,如图从a到b曲线是上升的,说函数f(x)在区间(a,b)上是增函数; 从b到c曲线是下降的,
说函数f(x)在区间(b,c)上
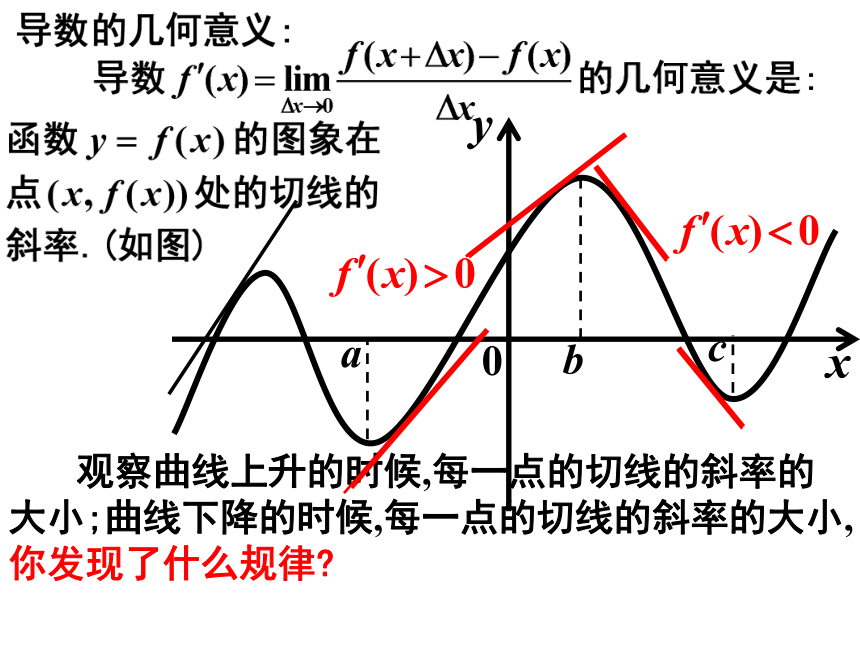
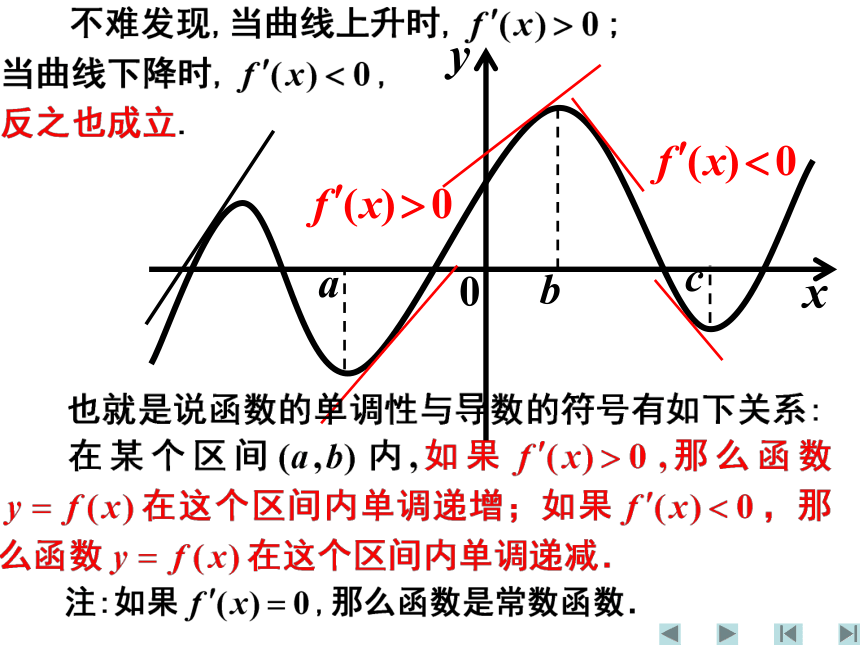
是减函数. 观察曲线上升的时候,每一点的切线的斜率的大小;曲线下降的时候,每一点的切线的斜率的大小,你发现了什么规律? 考察函数的单调性与导数的关系:2yx0.......观察函数y=x2-4x+3的图象: 总结:
该函数在区间(-∞,2)上单调递减,切线斜率小于0,即其导数为负; 该函数在区间(2,+∞)上单调递增,切线斜率大于0,即其导数为正. 而当x=2时其切线斜率为0,即导数为0.我们称它为“临界点”.注:如果在某个区间内恒有 ,则f(x)为常数函数.导数的符号显示了函数值变化的增减情况.
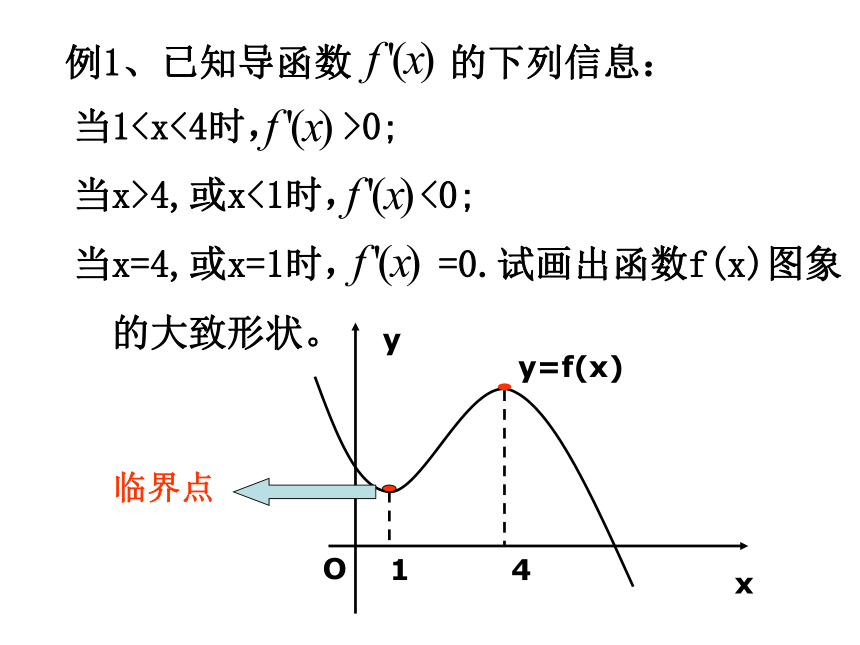
(如课本例1(自学))例1、已知导函数 的下列信息:当10;
当x>4,或x<1时, <0;
当x=4,或x=1时, =0.试画出函数f(x)图象
的大致形状。临界点问题2 法一:可用定义证明.法二:运用导数来证明(2)作差f(x1)-f(x2),并变形.由定义证明函数的单调性的一般步骤:(1)设x1、x2是给定区间的任意两个值,且x1
解不等式 ,得函数单调减区间.2答案练习1.判定函数 y=ex-x 的单调区间.解: =ex-1
当ex-1>0时,解得 x>0.
则函数的单调递增区间为(0,+∞).
当ex-1<0时,解得x<0.
即函数的单调递减区间为(-∞,0).有了导数看二次函数的单调性就很清楚自我小结一下运用导数研究单调性的方法步骤小结:利用导数确定函数的单调区间的步骤1.确定函数f(x)的定义域D.2.求出函数的导数f ′(x).3.解不等式组 ,得函数单调增区间;
解不等式 ,得函数单调减区间. 练习:确定函数 ,在哪个区间是增函数,那个区间是减函数。∴单调递增区间为: (2,+∞) 、 (-∞,0)
单调递减区间为: (0,2)例2、判断下列函数的单调性,并求出单调区间。
说函数f(x)在区间(b,c)上
是减函数. 观察曲线上升的时候,每一点的切线的斜率的大小;曲线下降的时候,每一点的切线的斜率的大小,你发现了什么规律? 考察函数的单调性与导数的关系:2yx0.......观察函数y=x2-4x+3的图象: 总结:
该函数在区间(-∞,2)上单调递减,切线斜率小于0,即其导数为负; 该函数在区间(2,+∞)上单调递增,切线斜率大于0,即其导数为正. 而当x=2时其切线斜率为0,即导数为0.我们称它为“临界点”.注:如果在某个区间内恒有 ,则f(x)为常数函数.导数的符号显示了函数值变化的增减情况.
(如课本例1(自学))例1、已知导函数 的下列信息:当1
当x>4,或x<1时, <0;
当x=4,或x=1时, =0.试画出函数f(x)图象
的大致形状。临界点问题2 法一:可用定义证明.法二:运用导数来证明(2)作差f(x1)-f(x2),并变形.由定义证明函数的单调性的一般步骤:(1)设x1、x2是给定区间的任意两个值,且x1
解不等式 ,得函数单调减区间.2答案练习1.判定函数 y=ex-x 的单调区间.解: =ex-1
当ex-1>0时,解得 x>0.
则函数的单调递增区间为(0,+∞).
当ex-1<0时,解得x<0.
即函数的单调递减区间为(-∞,0).有了导数看二次函数的单调性就很清楚自我小结一下运用导数研究单调性的方法步骤小结:利用导数确定函数的单调区间的步骤1.确定函数f(x)的定义域D.2.求出函数的导数f ′(x).3.解不等式组 ,得函数单调增区间;
解不等式 ,得函数单调减区间. 练习:确定函数 ,在哪个区间是增函数,那个区间是减函数。∴单调递增区间为: (2,+∞) 、 (-∞,0)
单调递减区间为: (0,2)例2、判断下列函数的单调性,并求出单调区间。
