新疆疏附县第二中学2021-2022学年高一上学期开学考试数学试题(含解析)
文档属性
| 名称 | 新疆疏附县第二中学2021-2022学年高一上学期开学考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 20:40:11 | ||
图片预览




文档简介
新疆疏附县第二中学2021-2022学年高一上学期开学考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知关于x的一元二次方程的两个实数根为,,且,则m的值为( )
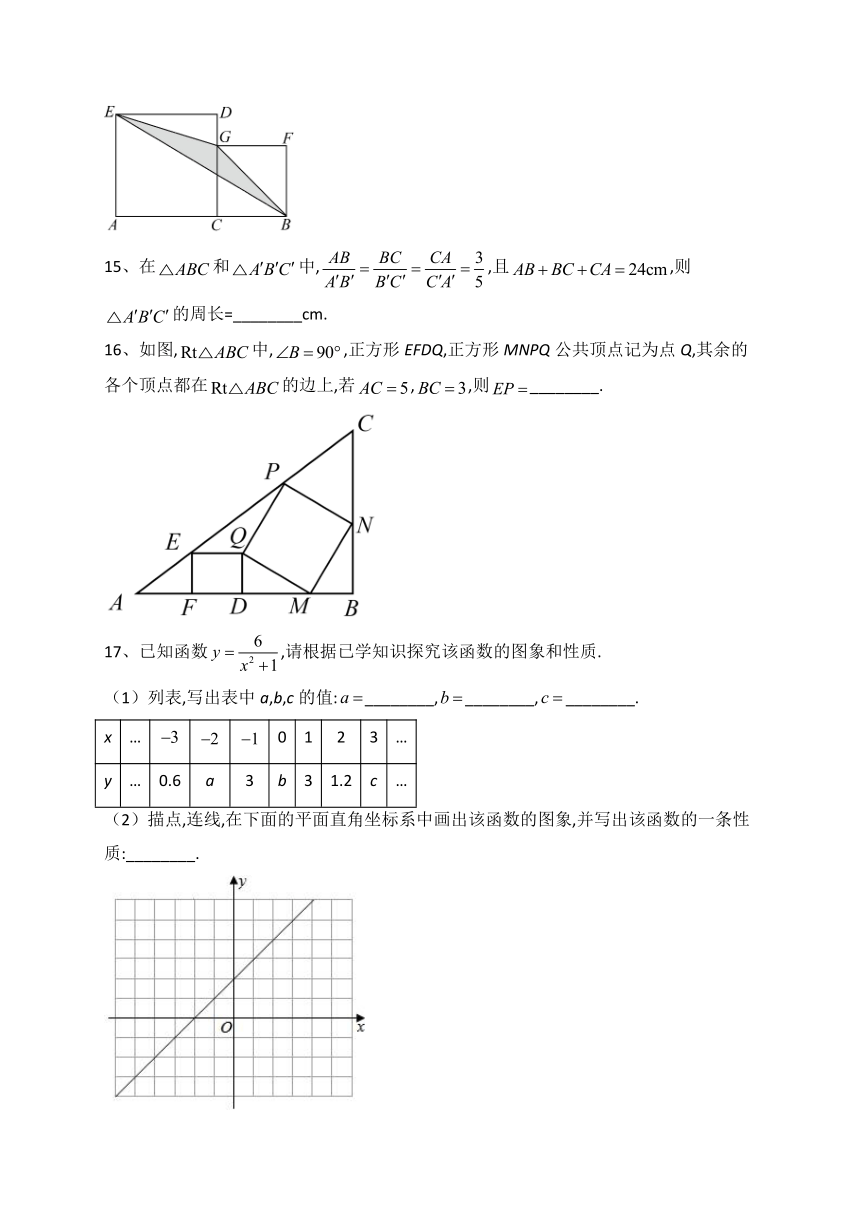
A.10或 B. C.10 D.
2、若集合至多含有一个元素,则a的取值范围是( ).
A. B. C. D.
3、如图所示,已知ABCD是长方形,且,,P是AD(含端点)上一动点,连接BP,则的取值范围为( )
A. B. C. D.
4、把分解因式,结果正确的是( )
A. B. C. D.
5、若二次根式有意义,且关于x的分式方程有正数解,则符合条件的整数m的和是( )
A. B. C. D.
6、关于x的分式方程的解为正数,且使关于y的一元一次不等式组有解,则所有满足条件的整数a的值之和为( )
A. B. C. D.
7、已知二次函数的图象如图所示,对称轴是直线,下列结论:①;
②;
③;
④,其中正确的是( )
A.①② B.只有① C.③④ D.①④
8、如图,BC为圆O的直径,弦于点E,直线l切圆O于点C,延长交l于点F,若,,则CF的长度为( )
A.2 B. C. D.4
9、如图,正方形ABCD中,,点E在边CD上,且.将沿AE对折至,延长EF交边BC于点G,连结AG,CF下列结论:
(1);
(2);
(3);
(4).其中正确结论的个数是( )
A.4 B.3 C.2 D.1
10、若存在正实数y,使得,则实数x的最大值为( )
A. B. C.1 D.4
11、甲,乙两个同学对问题“已知,,若关于x的实系数一元二次方程的两个根,,满足,求实数p的值”,各自提出一个猜测:
甲说:“对于任意一组m,n的值,p的不同值最多有4个;”
乙说:“存在一组m,n的值,使得p的不同值恰有3个;”
则下列选项正确的是( )
A.甲的猜测正确,乙的猜测错误 B.甲的猜测错误,乙的猜测正确
C.甲,乙的猜测都正确 D.甲,乙的猜测都错误
12、已知函数,若关于x的方程有四个不同的根,则实数t的取值范围是( )
A. B. C. D.
二、填空题
13、如图,已知圆O的面积为,AB为直径,弧AC的度数(劣弧AC所对圆心角的度数)为,弧BD的度数为,点P为直径AB上任一点,则的最小值为________.
14、如图,点C是线段AB上的一点,分别以AC BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG BG BE,当时,的面积记为;当时,的面积记为,……,以此类推,当时,的面积记为,则的值为________.
15、在和中,,且,则的周长=________cm.
16、如图,中,,正方形EFDQ,正方形MNPQ公共顶点记为点Q,其余的各个顶点都在的边上,若,,则________.
17、已知函数,请根据已学知识探究该函数的图象和性质.
(1)列表,写出表中a,b,c的值:________,________,________.
x … 0 1 2 3 …
y … 0.6 a 3 b 3 1.2 c …
(2)描点,连线,在下面的平面直角坐标系中画出该函数的图象,并写出该函数的一条性质:________.
(3)已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集:________.
三、解答题
18、如图,在四边形ABCD中,,,,,动点P从D开始沿DC边向C点以1cm/s的速度运动,动点Q从点B开始沿BA向A点以3cm/s的速度运动,P,Q分别从点D,B同时出发,当其中一点到达终点时,另一点也随之停止运动,运动的时间为t秒.
(1)t为何值时,四边形DPQA为矩形
(2)t为何值时,四边形PQBC为平行四边形
19、已知关于x的一元二次方程
(1)时,求证:方程一定有两个实数根.
(2)有甲 乙两个不透明的布袋,甲袋中装有3个除数字外完全相同的小球,分别标有数字1,2,3,乙袋中装有4个除数字外完全相同的小球,分别标有数字1,2,3,4,从甲袋中随机抽取一个小球,记录标有的数字为b,从乙袋中随机抽取一个小球,记录标有的数字为c,利用列表法或者树状图,求b,c的值使方程两个相等的实数根的概率.
20、如图,已知中,,,.点P是CB边上的一点,且,是的外接圆.
(1)求证:;
(2)判断与直线AC的位置关系,并说明理由;
21、在平面直角坐标系xOy中,我们称横从坐标都是整数的点为整点,若坐标系内两个整点,满足关于x的多项式能够因式分解为,则称点B是A的分解点.例如,满足,所以B是A的分解点.
(1)在点,,中,请找出不存在分解点的点__________;
(2)点P,Q在纵轴上(P在Q的上方),点R在横轴上,且点P,Q,R都存在分解点,若面积为6,请直接写出满足条件的的个数及每个三角形的顶点坐标;
(3)已知点D在第一象限内,D是C的分解点,请探究是否可能是等腰三角形 若可能请求出所有满足条件的点D的坐标;若不可能,请说明理由.
22、如图,在平面直角坐标系中,对称轴为直线的抛物线与x轴交于A,B两点,其中点A的坐标为,与y轴交于点,作直线AC.
(1)求抛物线的解析式;
(2)如图,点D是直线AC下方抛物线上的一个动点,连结DA,DC.当面积最大时,求点D的坐标;
(3)如图,在(2)的条件下,过点D作于点E,交y轴于点F,将绕点旋转得到,在旋转过程中,当点或点落在y轴上(不与点C,F重合)时,将,沿射线平移得到,在平移过程中,平面内是否存在点G,使得四边形是菱形 若存在,请直接写出所有符合条件的点G的坐标;若不存在,请说明理由.
参考答案
1、答案:B
解析:因为关于的一元二次方程的两个实数根为,,
所以,,
由且,
可得:,即,
解得:或,
因为,可得,
所以,
故选:B.
2、答案:B
解析:因为集合至多含有一个元素,
所以时,,此时满足题意;
当时,要满足题意,需方程无实根或两相等实根,
即,所以.
综上知,a的取值范围是.
故选:B.
3、答案:C
解析:,
又,,
故的取值范围为,
故选:C.
4、答案:D
解析:由题意,
故选:D
5、答案:D
解析:由去分母得:,
解得,
关于x的分式方程有正数解,
则,解得,
又是增根,当时,,即,
所以,
由二次根式有意义,则,解得,
因此且,
因为m为整数,
所以m可以为:,,,0,1,2,
所以符合条件的整数m的和是,
故选:D
6、答案:D
解析:由方程知:,且方程可整理为,
方程的解为正数,而时无解,
.
又,得有解,即,
.
综上,当时,;当时,;当时,;当时,;当时,;均满足条件.
所有满足条件的整数a的值之和为.
故选:D
7、答案:D
解析:由图象知的两根,满足,,则,
,,,,,因此,①正确;
,,②错误;
时,,③错误;
时,,④正确.
故选:D.
8、答案:B
解析:因为BC为圆O的直径,,
所以,,
所以,
故为等腰直角三角形,有,
所以,
又直线l切圆O于点C,所以,
故为等腰直角三角形,有,
因为,所以.
故选:B
9、答案:B
解析:(1),
;故(1)正确
(2),
设,则.
在中,根据勾股定理,得,
解得
.故(2)正确
(3),,
,
是等腰三角形,.
又;
,
;故(3)正确.
(4),,故.
故(4)错误.
∴正确的个数有3个.
故选:B.
10、答案:A
解析:,
因为,所以,所以,
当时,,解得,
当时,,解得,
故x的最大值为.
故选:A
11、答案:C
解析:实系数一元二次方程,则,
当时,,则与条件矛盾,
当时,,,
可得有两个值,
当时,,,
可得有一个或两个值.
综上可知,
当时,p的值有3个,
当时,p的值有4个,
所以甲,乙二人的猜测都正确.
故选:.
12、答案:B
解析:设,
,
,
当时,,m递增;当时,,m递减;在时,,m取得极大值.
当时,,m递减.
可得m图象如图,
由图知:当时,直线与m图象有一个交点;当时,直线与m图象有三个交点.
故关于m的二次方程有两根,,且,,方满足题意.
设,
则:,
解得:,
故选B.
13、答案:3
解析:设圆O的半径为r,
∵圆O的面积为,
,即.
作点C关于AB的对称点,连接OD,,,如图,
则的长即为的最小值,
的度数为,
,
,
,
,
,
,即的最小值为3.
故答案为:3
14、答案:
解析:连接EC,
正方形ACDE和正方形CBFG,
,
和是同底(BG)等高的三角形,即,
当时,,
故答案为:
15、答案:40
解析:因为,
所以,
所以,
所以.
所以的周长.
故答案为:40
16、答案:
解析:在中,,,,由勾股定理得:,
过P作于G,
∵四边形EFDQ和四边形QMNP是正方形,
,,
,,
,
同理,
在,,中,
,,,
,
,,
,
,
,
同理,,
设,则,,,,,
可列一元二次方程组:
解得:
.
17、答案:(1)1.2,6,0.6;
(2)图象见解析,函数关于y轴对称;
(3)图象见解析,.
解析:(1)当时,,
当时,,
当时,=0.6,
故答案为:1.2,6,0.6;
(2)如图所示:
性质:函数关于y轴对称;(答案不唯一:或函数有最大值是6);
故答案为:函数关于y轴对称;
(3)由图象得:不等式的解集是:;
故答案为:.
18、答案:(1);
(2)6.
解析:(1)当DPQA为矩形时,,
,,,
,解得,
当时,四边形DPQA为矩形.
(2)当四边形DQBC为平行四边形时,,
,,,
,解得,
时,四边形DQBC为平行四边形.
19、答案:(1)证明见解析;
(2).
解析:(1)证明:,
时,方程有两个相等的实数根;时,方程有两个不相等的实数根
故方程一定有两个实数根;
(2)画树状图得:
共有12种等可能的结果,若方程有两个相等的实数根,,
,满足条件的结果有和,共2种,
,c的值使方程两个相等的实数根的概率为.
20、答案:(1)证明见解析;
(2)与直线AC相切,理由见解析.
解析:(1)证明:在中,,,,
,
,,都是锐角,
.
(2)与直线AC相切.
理由:作的直径AD,连接PD,如图所示,
是的直径,,,
,,
由(1)知,,,
是的直径,与直线AC相切.
21、答案:(1);
(2)答案见解析;
(3)不可能为等腰三角形,理由见解析.
解析:(1)对于,,故是的分解点.
对于,方程无实解,故不存在分解点.
对于,,故是的分解点.
点不存在分解点;
(2),Q在纵轴上,P,Q都存在分解点,,Q的纵坐标只能是0,,,,
因为,可得,故OR为的正约数.
当时,,在Q的上方,,,
同理当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
综上所迖,的个数为8;
(3)如图,设,则m,n是正整数,
且D为C的分解点,
当时,,,此时,不可能构成等腰三角形;
当时,则,,则点C必在直线,相交直线的右上角区域,
此时,,若为等腰三角形,只可能,
如图,过C作CN垂直于直线,过点D作轴于M.
在和中,,若,则,
,即,此式子可以化为,
,n为正整数,则,即,,
此时O,C,D共线,不存在,
综上所述,不可能为等腰三角形.
22、答案:(1);
(2);
(3)所有符合条件的点G坐标为或
解析:(1)抛物线对称轴为.
且点A的坐标为.点C的坐标为
.解得
抛物线的解析式为
(2)过D作轴交AC于H.设,
设AC的解析式为,则,解得.
故AC的解析式为.则
则.
故当时,取最大值.此时.
(3)存在,所有符合条件的G坐标为,.
提示:,,,.
①当落在y轴上时,如图,点,,
设平移距离是2t,则,.
由得,解得.
此时,,所以.
②当落在y轴上时,如图,点,,
设平移距离是2t,则,.
由得,解得.
此时,,所以.
综上所述,所有符合条件的点G坐标为或.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知关于x的一元二次方程的两个实数根为,,且,则m的值为( )
A.10或 B. C.10 D.
2、若集合至多含有一个元素,则a的取值范围是( ).
A. B. C. D.
3、如图所示,已知ABCD是长方形,且,,P是AD(含端点)上一动点,连接BP,则的取值范围为( )
A. B. C. D.
4、把分解因式,结果正确的是( )
A. B. C. D.
5、若二次根式有意义,且关于x的分式方程有正数解,则符合条件的整数m的和是( )
A. B. C. D.
6、关于x的分式方程的解为正数,且使关于y的一元一次不等式组有解,则所有满足条件的整数a的值之和为( )
A. B. C. D.
7、已知二次函数的图象如图所示,对称轴是直线,下列结论:①;
②;
③;
④,其中正确的是( )
A.①② B.只有① C.③④ D.①④
8、如图,BC为圆O的直径,弦于点E,直线l切圆O于点C,延长交l于点F,若,,则CF的长度为( )
A.2 B. C. D.4
9、如图,正方形ABCD中,,点E在边CD上,且.将沿AE对折至,延长EF交边BC于点G,连结AG,CF下列结论:
(1);
(2);
(3);
(4).其中正确结论的个数是( )
A.4 B.3 C.2 D.1
10、若存在正实数y,使得,则实数x的最大值为( )
A. B. C.1 D.4
11、甲,乙两个同学对问题“已知,,若关于x的实系数一元二次方程的两个根,,满足,求实数p的值”,各自提出一个猜测:
甲说:“对于任意一组m,n的值,p的不同值最多有4个;”
乙说:“存在一组m,n的值,使得p的不同值恰有3个;”
则下列选项正确的是( )
A.甲的猜测正确,乙的猜测错误 B.甲的猜测错误,乙的猜测正确
C.甲,乙的猜测都正确 D.甲,乙的猜测都错误
12、已知函数,若关于x的方程有四个不同的根,则实数t的取值范围是( )
A. B. C. D.
二、填空题
13、如图,已知圆O的面积为,AB为直径,弧AC的度数(劣弧AC所对圆心角的度数)为,弧BD的度数为,点P为直径AB上任一点,则的最小值为________.
14、如图,点C是线段AB上的一点,分别以AC BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG BG BE,当时,的面积记为;当时,的面积记为,……,以此类推,当时,的面积记为,则的值为________.
15、在和中,,且,则的周长=________cm.
16、如图,中,,正方形EFDQ,正方形MNPQ公共顶点记为点Q,其余的各个顶点都在的边上,若,,则________.
17、已知函数,请根据已学知识探究该函数的图象和性质.
(1)列表,写出表中a,b,c的值:________,________,________.
x … 0 1 2 3 …
y … 0.6 a 3 b 3 1.2 c …
(2)描点,连线,在下面的平面直角坐标系中画出该函数的图象,并写出该函数的一条性质:________.
(3)已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集:________.
三、解答题
18、如图,在四边形ABCD中,,,,,动点P从D开始沿DC边向C点以1cm/s的速度运动,动点Q从点B开始沿BA向A点以3cm/s的速度运动,P,Q分别从点D,B同时出发,当其中一点到达终点时,另一点也随之停止运动,运动的时间为t秒.
(1)t为何值时,四边形DPQA为矩形
(2)t为何值时,四边形PQBC为平行四边形
19、已知关于x的一元二次方程
(1)时,求证:方程一定有两个实数根.
(2)有甲 乙两个不透明的布袋,甲袋中装有3个除数字外完全相同的小球,分别标有数字1,2,3,乙袋中装有4个除数字外完全相同的小球,分别标有数字1,2,3,4,从甲袋中随机抽取一个小球,记录标有的数字为b,从乙袋中随机抽取一个小球,记录标有的数字为c,利用列表法或者树状图,求b,c的值使方程两个相等的实数根的概率.
20、如图,已知中,,,.点P是CB边上的一点,且,是的外接圆.
(1)求证:;
(2)判断与直线AC的位置关系,并说明理由;
21、在平面直角坐标系xOy中,我们称横从坐标都是整数的点为整点,若坐标系内两个整点,满足关于x的多项式能够因式分解为,则称点B是A的分解点.例如,满足,所以B是A的分解点.
(1)在点,,中,请找出不存在分解点的点__________;
(2)点P,Q在纵轴上(P在Q的上方),点R在横轴上,且点P,Q,R都存在分解点,若面积为6,请直接写出满足条件的的个数及每个三角形的顶点坐标;
(3)已知点D在第一象限内,D是C的分解点,请探究是否可能是等腰三角形 若可能请求出所有满足条件的点D的坐标;若不可能,请说明理由.
22、如图,在平面直角坐标系中,对称轴为直线的抛物线与x轴交于A,B两点,其中点A的坐标为,与y轴交于点,作直线AC.
(1)求抛物线的解析式;
(2)如图,点D是直线AC下方抛物线上的一个动点,连结DA,DC.当面积最大时,求点D的坐标;
(3)如图,在(2)的条件下,过点D作于点E,交y轴于点F,将绕点旋转得到,在旋转过程中,当点或点落在y轴上(不与点C,F重合)时,将,沿射线平移得到,在平移过程中,平面内是否存在点G,使得四边形是菱形 若存在,请直接写出所有符合条件的点G的坐标;若不存在,请说明理由.
参考答案
1、答案:B
解析:因为关于的一元二次方程的两个实数根为,,
所以,,
由且,
可得:,即,
解得:或,
因为,可得,
所以,
故选:B.
2、答案:B
解析:因为集合至多含有一个元素,
所以时,,此时满足题意;
当时,要满足题意,需方程无实根或两相等实根,
即,所以.
综上知,a的取值范围是.
故选:B.
3、答案:C
解析:,
又,,
故的取值范围为,
故选:C.
4、答案:D
解析:由题意,
故选:D
5、答案:D
解析:由去分母得:,
解得,
关于x的分式方程有正数解,
则,解得,
又是增根,当时,,即,
所以,
由二次根式有意义,则,解得,
因此且,
因为m为整数,
所以m可以为:,,,0,1,2,
所以符合条件的整数m的和是,
故选:D
6、答案:D
解析:由方程知:,且方程可整理为,
方程的解为正数,而时无解,
.
又,得有解,即,
.
综上,当时,;当时,;当时,;当时,;当时,;均满足条件.
所有满足条件的整数a的值之和为.
故选:D
7、答案:D
解析:由图象知的两根,满足,,则,
,,,,,因此,①正确;
,,②错误;
时,,③错误;
时,,④正确.
故选:D.
8、答案:B
解析:因为BC为圆O的直径,,
所以,,
所以,
故为等腰直角三角形,有,
所以,
又直线l切圆O于点C,所以,
故为等腰直角三角形,有,
因为,所以.
故选:B
9、答案:B
解析:(1),
;故(1)正确
(2),
设,则.
在中,根据勾股定理,得,
解得
.故(2)正确
(3),,
,
是等腰三角形,.
又;
,
;故(3)正确.
(4),,故.
故(4)错误.
∴正确的个数有3个.
故选:B.
10、答案:A
解析:,
因为,所以,所以,
当时,,解得,
当时,,解得,
故x的最大值为.
故选:A
11、答案:C
解析:实系数一元二次方程,则,
当时,,则与条件矛盾,
当时,,,
可得有两个值,
当时,,,
可得有一个或两个值.
综上可知,
当时,p的值有3个,
当时,p的值有4个,
所以甲,乙二人的猜测都正确.
故选:.
12、答案:B
解析:设,
,
,
当时,,m递增;当时,,m递减;在时,,m取得极大值.
当时,,m递减.
可得m图象如图,
由图知:当时,直线与m图象有一个交点;当时,直线与m图象有三个交点.
故关于m的二次方程有两根,,且,,方满足题意.
设,
则:,
解得:,
故选B.
13、答案:3
解析:设圆O的半径为r,
∵圆O的面积为,
,即.
作点C关于AB的对称点,连接OD,,,如图,
则的长即为的最小值,
的度数为,
,
,
,
,
,
,即的最小值为3.
故答案为:3
14、答案:
解析:连接EC,
正方形ACDE和正方形CBFG,
,
和是同底(BG)等高的三角形,即,
当时,,
故答案为:
15、答案:40
解析:因为,
所以,
所以,
所以.
所以的周长.
故答案为:40
16、答案:
解析:在中,,,,由勾股定理得:,
过P作于G,
∵四边形EFDQ和四边形QMNP是正方形,
,,
,,
,
同理,
在,,中,
,,,
,
,,
,
,
,
同理,,
设,则,,,,,
可列一元二次方程组:
解得:
.
17、答案:(1)1.2,6,0.6;
(2)图象见解析,函数关于y轴对称;
(3)图象见解析,.
解析:(1)当时,,
当时,,
当时,=0.6,
故答案为:1.2,6,0.6;
(2)如图所示:
性质:函数关于y轴对称;(答案不唯一:或函数有最大值是6);
故答案为:函数关于y轴对称;
(3)由图象得:不等式的解集是:;
故答案为:.
18、答案:(1);
(2)6.
解析:(1)当DPQA为矩形时,,
,,,
,解得,
当时,四边形DPQA为矩形.
(2)当四边形DQBC为平行四边形时,,
,,,
,解得,
时,四边形DQBC为平行四边形.
19、答案:(1)证明见解析;
(2).
解析:(1)证明:,
时,方程有两个相等的实数根;时,方程有两个不相等的实数根
故方程一定有两个实数根;
(2)画树状图得:
共有12种等可能的结果,若方程有两个相等的实数根,,
,满足条件的结果有和,共2种,
,c的值使方程两个相等的实数根的概率为.
20、答案:(1)证明见解析;
(2)与直线AC相切,理由见解析.
解析:(1)证明:在中,,,,
,
,,都是锐角,
.
(2)与直线AC相切.
理由:作的直径AD,连接PD,如图所示,
是的直径,,,
,,
由(1)知,,,
是的直径,与直线AC相切.
21、答案:(1);
(2)答案见解析;
(3)不可能为等腰三角形,理由见解析.
解析:(1)对于,,故是的分解点.
对于,方程无实解,故不存在分解点.
对于,,故是的分解点.
点不存在分解点;
(2),Q在纵轴上,P,Q都存在分解点,,Q的纵坐标只能是0,,,,
因为,可得,故OR为的正约数.
当时,,在Q的上方,,,
同理当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
当时,可得,,
综上所迖,的个数为8;
(3)如图,设,则m,n是正整数,
且D为C的分解点,
当时,,,此时,不可能构成等腰三角形;
当时,则,,则点C必在直线,相交直线的右上角区域,
此时,,若为等腰三角形,只可能,
如图,过C作CN垂直于直线,过点D作轴于M.
在和中,,若,则,
,即,此式子可以化为,
,n为正整数,则,即,,
此时O,C,D共线,不存在,
综上所述,不可能为等腰三角形.
22、答案:(1);
(2);
(3)所有符合条件的点G坐标为或
解析:(1)抛物线对称轴为.
且点A的坐标为.点C的坐标为
.解得
抛物线的解析式为
(2)过D作轴交AC于H.设,
设AC的解析式为,则,解得.
故AC的解析式为.则
则.
故当时,取最大值.此时.
(3)存在,所有符合条件的G坐标为,.
提示:,,,.
①当落在y轴上时,如图,点,,
设平移距离是2t,则,.
由得,解得.
此时,,所以.
②当落在y轴上时,如图,点,,
设平移距离是2t,则,.
由得,解得.
此时,,所以.
综上所述,所有符合条件的点G坐标为或.
同课章节目录
