勾股定理
图片预览





文档简介
课件30张PPT。18.1 勾股定理台州初级中学数学组 王飞兵金秋十月
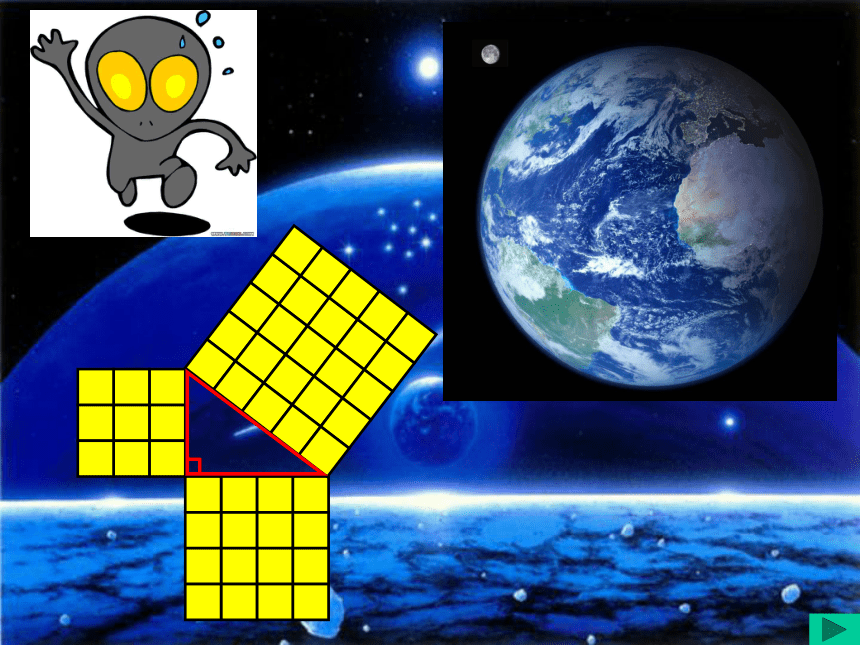
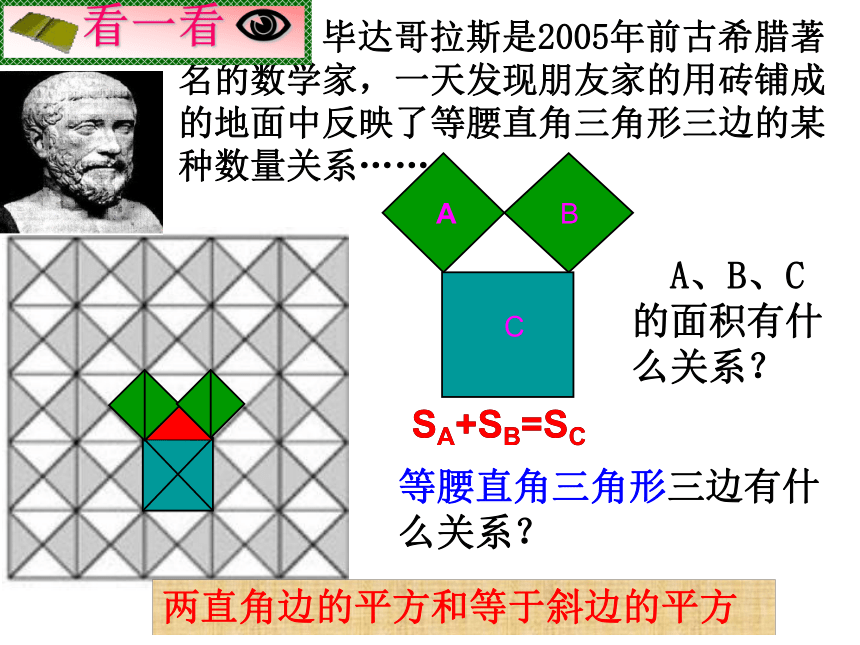
嫦娥奔月弦图这个图形里蕴涵着怎样博大精深的知识呢? 它标志着我国古代数学的伟大成就! A、B、C的面积有什么关系?等腰直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方 毕达哥拉斯是2005年前古希腊著名的数学家,一天发现朋友家的用砖铺成的地面中反映了等腰直角三角形三边的某种数量关系……SA+SB=SCABC图2图3491392534sA+sB=sC两直角边的平方和
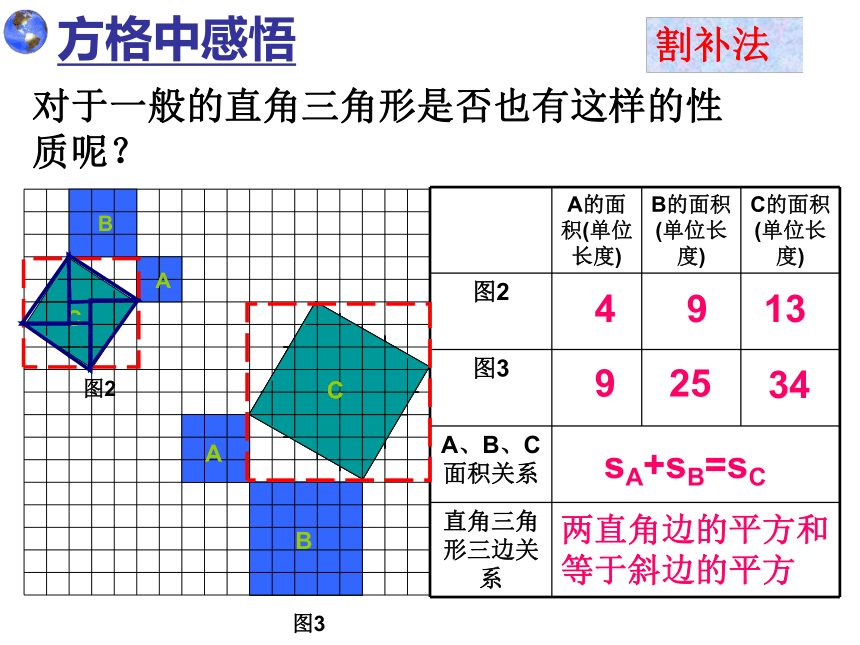
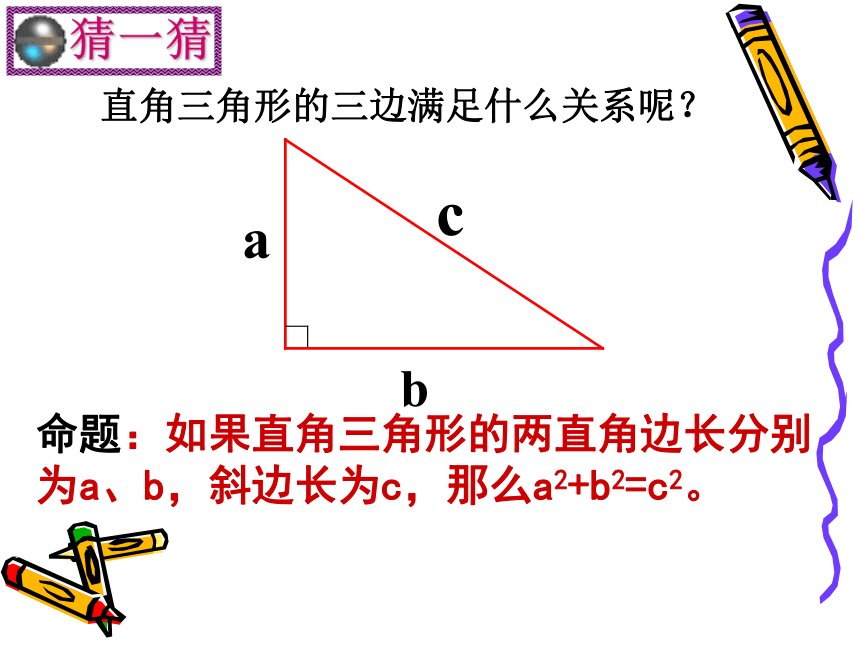
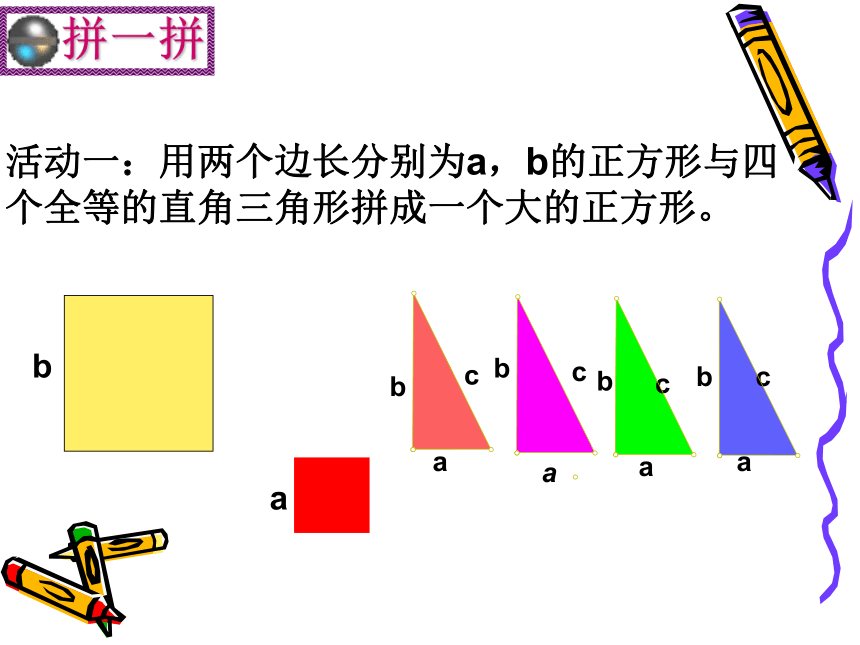
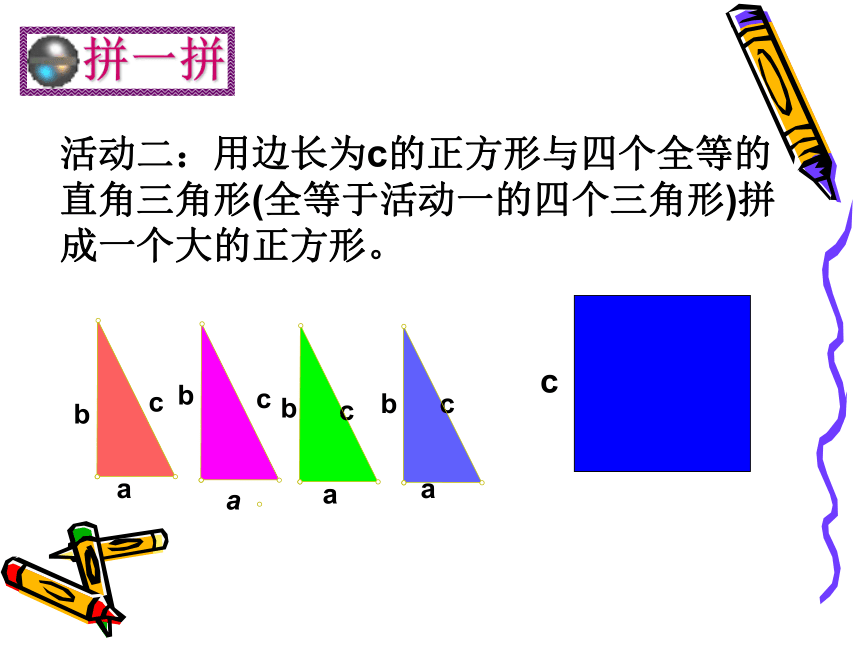
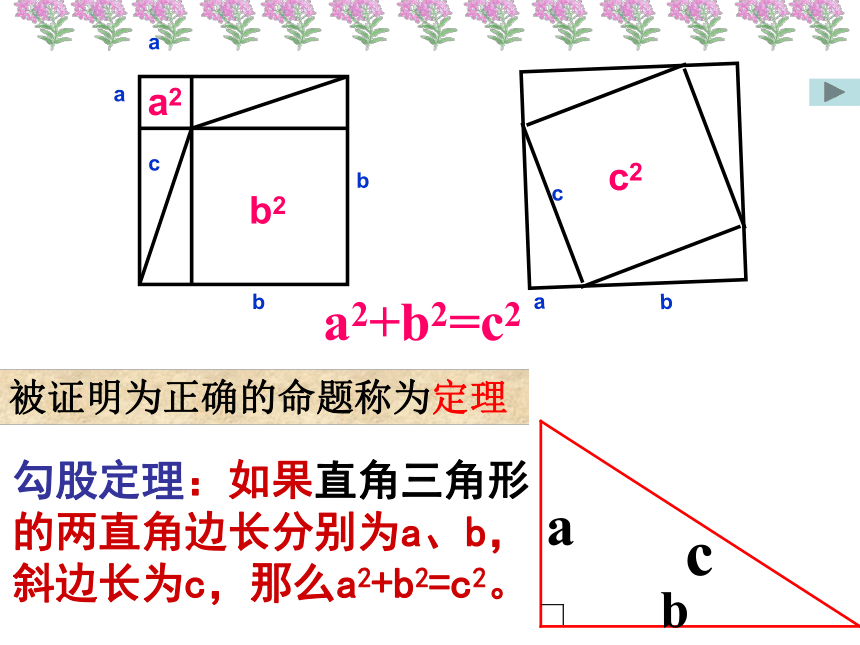
等于斜边的平方 方格中感悟对于一般的直角三角形是否也有这样的性质呢?割补法命题:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。直角三角形的三边满足什么关系呢?活动一:用两个边长分别为a,b的正方形与四个全等的直角三角形拼成一个大的正方形。活动二:用边长为c的正方形与四个全等的直角三角形(全等于活动一的四个三角形)拼成一个大的正方形。被证明为正确的命题称为定理勾股定理:如果直角三角形
的两直角边长分别为a、b,
斜边长为c,那么a2+b2=c2。a2b2c2a2+b2=c2勾股定理学习目标:了解勾股定理的由来,经历探索勾股定理的过程.理解并能用不同的方法证明勾股定理,并能简单的运用.提高推理意识与探究习惯,感受我国古代数学的伟大成就. 在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾 股 定 理abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧!证法二:赵爽弦图证明勾股定理证法三:=c数形结合思想 等 积 变 换ba美国总统的故事加菲尔德(James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关数学结论证法四:aabbcc总统证法:∴ a2 + b2 = c2勾 股 知 识 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。 商高定理就是勾股定理哦!毕达哥拉斯定理: 毕达哥拉斯 “勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.
相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”. 毕达哥拉斯(毕达哥拉斯,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年. 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2 及时检验1、求下图中字母所代表的正方形的面积。225400A6252.求下列图中表示边的未知数x、y的值.81144xy比一比看看谁算得快!4.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x17125x方程思想如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为____cm2。49拓展延伸FE数学的和谐美新闻快递浙江在线12月15日迅 12月12日温州温富大厦发生重大火灾事故,当消防队员赶来时,需要到二楼的高度救火,每层楼高3米,消防队员取来7米长的云梯,如果梯子的底部须距离墙基2米才能放稳,消防队员能达到二楼的高度灭火吗?这堂课 ...的收获:颗粒归仓你说,我说,大家说!1、本节课我们经历了怎样的学习过程? 经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。3、学了本节课后你有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。1、作业本(1) 作 业3 、利用方格纸探索锐角三角形或钝角三角形的三边关系。2 、上网查阅下列网址,写一篇关于勾股定理的小论文:http//:www.mmit.stc.sh.cn//ggdl.htmhttp//:www. Liangzhou.net/gougudinglihttp//:www. Qq12.com/flash/3427.het课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。敬请指导再 见
嫦娥奔月弦图这个图形里蕴涵着怎样博大精深的知识呢? 它标志着我国古代数学的伟大成就! A、B、C的面积有什么关系?等腰直角三角形三边有什么关系?SA+SB=SC两直角边的平方和等于斜边的平方 毕达哥拉斯是2005年前古希腊著名的数学家,一天发现朋友家的用砖铺成的地面中反映了等腰直角三角形三边的某种数量关系……SA+SB=SCABC图2图3491392534sA+sB=sC两直角边的平方和
等于斜边的平方 方格中感悟对于一般的直角三角形是否也有这样的性质呢?割补法命题:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。直角三角形的三边满足什么关系呢?活动一:用两个边长分别为a,b的正方形与四个全等的直角三角形拼成一个大的正方形。活动二:用边长为c的正方形与四个全等的直角三角形(全等于活动一的四个三角形)拼成一个大的正方形。被证明为正确的命题称为定理勾股定理:如果直角三角形
的两直角边长分别为a、b,
斜边长为c,那么a2+b2=c2。a2b2c2a2+b2=c2勾股定理学习目标:了解勾股定理的由来,经历探索勾股定理的过程.理解并能用不同的方法证明勾股定理,并能简单的运用.提高推理意识与探究习惯,感受我国古代数学的伟大成就. 在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾 股 定 理abcS大正方形=c2S小正方形=(b-a)2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧!证法二:赵爽弦图证明勾股定理证法三:=c数形结合思想 等 积 变 换ba美国总统的故事加菲尔德(James A. Garfield; 1831 ? 1881)1881 年成为美国第 20 任总统
1876 年提出有关数学结论证法四:aabbcc总统证法:∴ a2 + b2 = c2勾 股 知 识 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。 商高定理就是勾股定理哦!毕达哥拉斯定理: 毕达哥拉斯 “勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.
相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”. 毕达哥拉斯(毕达哥拉斯,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年. 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2 及时检验1、求下图中字母所代表的正方形的面积。225400A6252.求下列图中表示边的未知数x、y的值.81144xy比一比看看谁算得快!4.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x17125x方程思想如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为____cm2。49拓展延伸FE数学的和谐美新闻快递浙江在线12月15日迅 12月12日温州温富大厦发生重大火灾事故,当消防队员赶来时,需要到二楼的高度救火,每层楼高3米,消防队员取来7米长的云梯,如果梯子的底部须距离墙基2米才能放稳,消防队员能达到二楼的高度灭火吗?这堂课 ...的收获:颗粒归仓你说,我说,大家说!1、本节课我们经历了怎样的学习过程? 经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。3、学了本节课后你有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。1、作业本(1) 作 业3 、利用方格纸探索锐角三角形或钝角三角形的三边关系。2 、上网查阅下列网址,写一篇关于勾股定理的小论文:http//:www.mmit.stc.sh.cn//ggdl.htmhttp//:www. Liangzhou.net/gougudinglihttp//:www. Qq12.com/flash/3427.het课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。敬请指导再 见
