2014-2015学年高中人教A版数学选修2-2同步课件 2.2.1综合法和分析法
文档属性
| 名称 | 2014-2015学年高中人教A版数学选修2-2同步课件 2.2.1综合法和分析法 |  | |
| 格式 | zip | ||
| 文件大小 | 46.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-03 08:51:16 | ||
图片预览




文档简介
课件17张PPT。综合法和分析法通过前面的学习我们直到,合情推理多得出的结论我们需要加以证明,这正是数学区别于其他科学的显著特点.数学结论的正确性必须通过演绎推理(逻辑推理)的方式加以证明,本节我们来看一种基础的证明方法直接证明1.直接证明:直接证明包括两种最基本证明方法——
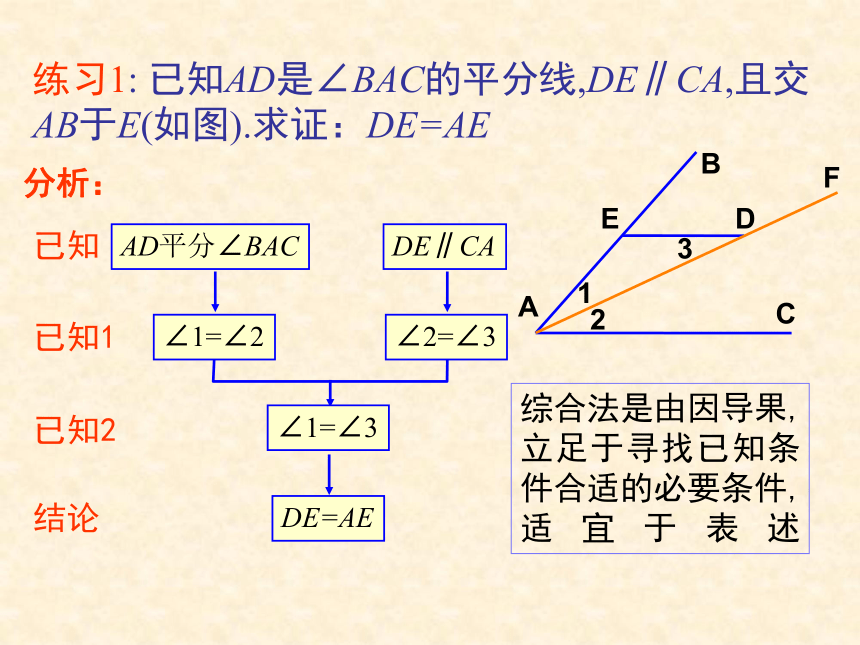
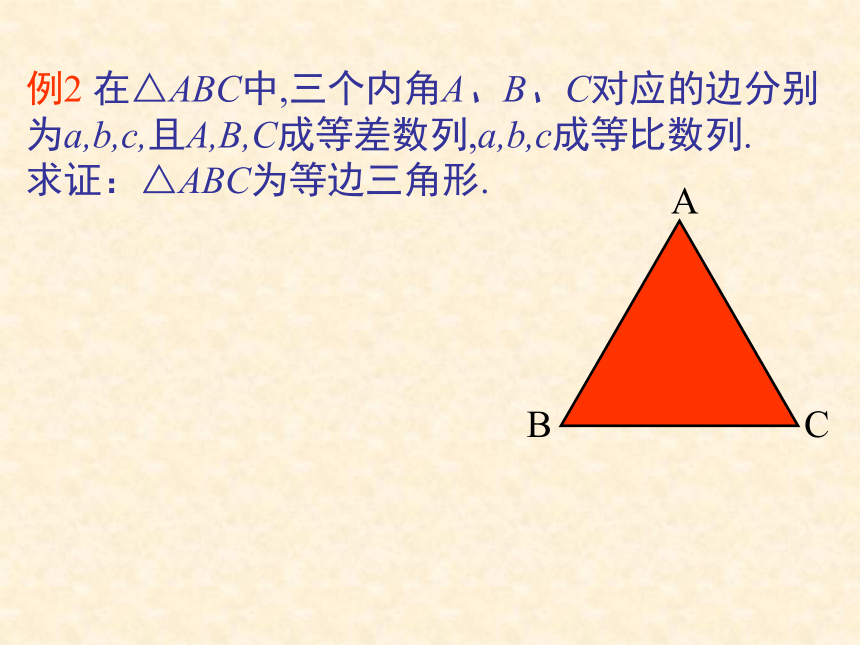
综合法与分析法综合法(synthetical methed):所谓综合法,是指“由因导果”的思想方法,即从已知条件出发,不断地展开思考,去探索结论的方法 .综合法的可概括为下面形式: 例1已知a,b>0,求证:a(b2+c2)+b(c2+a2)≥4abc.证明:∵b2+c2≥2bc,a>0∴a(b2+c2)≥2abc同理,∵c2+a2≥2ac,b>0∴b(a2+c2)≥2abc∴ a(b2+c2)+b(c2+a2)≥4abc练习1: 已知AD是∠BAC的平分线,DE∥CA,且交AB于E(如图).求证:DE=AE 分析:综合法是由因导果,立足于寻找已知条件合适的必要条件,适宜于表述 例2 在△ABC中,三个内角A、B、C对应的边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列.
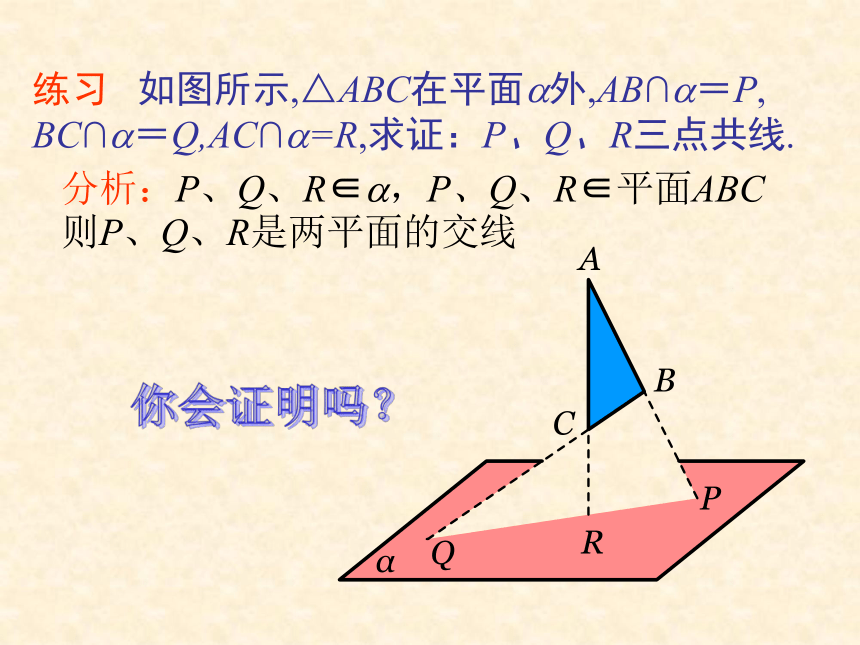
求证:△ABC为等边三角形.练习 如图所示,△ABC在平面?外,AB∩?=P, BC∩?=Q,AC∩?=R,求证:P、Q、R三点共线. 分析:P、Q、R∈?,P、Q、R∈平面ABC
则P、Q、R是两平面的交线你会证明吗?在解决实际问题时,经常要先作语言的变换文字语言图形语言符号语言然后在仔细分析题目的隐含条件,将隐含条件表示出来分析法(analytical methed):是指“由因导果”的思想方法,即从已知条件出发,不断地展开思考,去探索结论的方法. 分析:从待证不等式不易发现证明的出发点,因此我们直接从待证不等式出发,分析其成立的充分条件.例3 求证:证明:因为 都是正数,所以要证
分析:练习1: 已知AD是∠BAC的平分线,DE∥CA,且交AB于E(如图).求证:DE=AE .练习 2 设a,b,c为一个三角形的三边,
s=(a+b+c)/2,且s2=2ab. 求证:s<2as<2as=(a+b+c)/2b+c<3as2=2abb
综合法与分析法综合法(synthetical methed):所谓综合法,是指“由因导果”的思想方法,即从已知条件出发,不断地展开思考,去探索结论的方法 .综合法的可概括为下面形式: 例1已知a,b>0,求证:a(b2+c2)+b(c2+a2)≥4abc.证明:∵b2+c2≥2bc,a>0∴a(b2+c2)≥2abc同理,∵c2+a2≥2ac,b>0∴b(a2+c2)≥2abc∴ a(b2+c2)+b(c2+a2)≥4abc练习1: 已知AD是∠BAC的平分线,DE∥CA,且交AB于E(如图).求证:DE=AE 分析:综合法是由因导果,立足于寻找已知条件合适的必要条件,适宜于表述 例2 在△ABC中,三个内角A、B、C对应的边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列.
求证:△ABC为等边三角形.练习 如图所示,△ABC在平面?外,AB∩?=P, BC∩?=Q,AC∩?=R,求证:P、Q、R三点共线. 分析:P、Q、R∈?,P、Q、R∈平面ABC
则P、Q、R是两平面的交线你会证明吗?在解决实际问题时,经常要先作语言的变换文字语言图形语言符号语言然后在仔细分析题目的隐含条件,将隐含条件表示出来分析法(analytical methed):是指“由因导果”的思想方法,即从已知条件出发,不断地展开思考,去探索结论的方法. 分析:从待证不等式不易发现证明的出发点,因此我们直接从待证不等式出发,分析其成立的充分条件.例3 求证:证明:因为 都是正数,所以要证
分析:练习1: 已知AD是∠BAC的平分线,DE∥CA,且交AB于E(如图).求证:DE=AE .练习 2 设a,b,c为一个三角形的三边,
s=(a+b+c)/2,且s2=2ab. 求证:s<2as<2as=(a+b+c)/2b+c<3as2=2abb
