人教版数学八年级上册11.3.2多边形的内角和 教学设计(表格式)
文档属性
| 名称 | 人教版数学八年级上册11.3.2多边形的内角和 教学设计(表格式) | 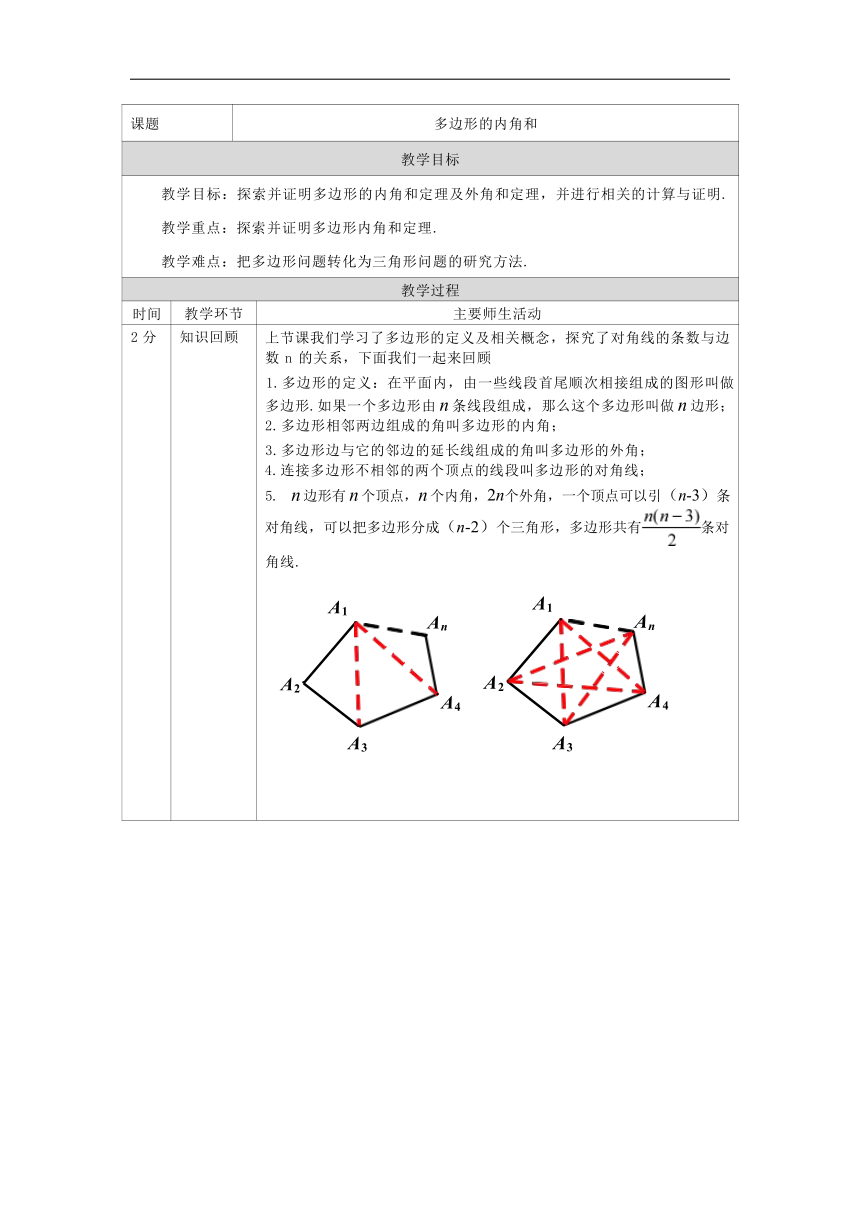 | |
| 格式 | docx | ||
| 文件大小 | 157.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 21:24:20 | ||
图片预览


文档简介
课题 多边形的内角和
教学目标
教学目标:探索并证明多边形的内角和定理及外角和定理,并进行相关的计算与证明. 教学重点:探索并证明多边形内角和定理. 教学难点:把多边形问题转化为三角形问题的研究方法.
教学过程
时间 教学环节 主要师生活动
2 分 知识回顾 上节课我们学习了多边形的定义及相关概念,探究了对角线的条数与边 数 n 的关系,下面我们一起来回顾 1.多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做 多边形.如果一个多边形由 n 条线段组成,那么这个多边形叫做 n 边形; 2.多边形相邻两边组成的角叫多边形的内角; 3.多边形边与它的邻边的延长线组成的角叫多边形的外角; 4.连接多边形不相邻的两个顶点的线段叫多边形的对角线; 5. n 边形有 n 个顶点,n 个内角,2n个外角,一个顶点可以引(n-3)条 对角线,可以把多边形分成(n-2)个三角形,多边形共有条对 角线.
A1 An A2 A4 A1 An A2 A4
A3 A3
14 分 探究新知 研究多边形的问题通过添加对角线,都可以转化为三角形.你能利用三 角形内角和定理证明,任意四边形 ABCD 的内角和等于 360。吗? 已知:四边形 ABCD ,求证: 经A+经B+经C+经D=360。. 方法 1:证明:连接AC , 经BAD + 经B + 经BCD + 经D = 经1+经2+经B + 经3 + 经4 + 经D = (经1+ 经B + 经3) + (经2 + 经D + 经4) = 180。+180。 = 360。 把一个四边形分成几个三角形,还有其他分法吗? 方法 2:如图,在四边形 ABCD 内部取一点 O , 连接 AO、BO、CO、DO 把四边形分成 四个三角形 ΔABO、ΔADO、ΔCDO、ΔCBO 所以四边形 ABCD的内角和为: 180。会 4 一 (经AOB + 经AOD + 经COD + 经COB) = 180。会 4 一 360。 = 360。 方法 3:如图,在BC 边上任取一点 O ,连接 AO、BO ,所以该四边形被分成三个三角形 ΔABO、ΔADO、ΔDCO 所以四边形 ABCD的内角和为: 180。会3 一 (经AOB + 经AOD + 经COD) = 180。会3 一 180。 = 360。 方法 4:如图,在四边形外任取一点 O , 连接 AO、BO、CO、DO 将四边形变成 有一个公共顶点的三个三角形 ΔABO、ΔADO、ΔDCO ,再减去 ΔCBO 的内角和 180,即可得四边形 ABCD 的内角和为: 180。会3 一 180。= 360。
例题解析 以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为 已学的三角形内角和进行求解. 四边形可以如此解决,多边形的问题也可以通过添加对角线转化成三角 形问题来解决. 如图 1 可得多边形的内角和为 (n - 2)×180。 如图 2 多边形的内角和 n × 180。-360。=(n - 2)×180。 如图 3 多边形的内角和(n-1)×180。-180。= (n - 2)×180。 如图 4 多边形的内角和(n-1)×180。-180。= (n - 2)×180。 通过探究得到多边形内角和公式为 (n - 2)×180。 小结: 多边形的问题可以转化为三角形的问题来研究,将未知转化为已知. 多边形的内角和仅与边数有关,与多边形的大小无关; 请问八边形的内角和是(8 - 2)×180。=1080。, 十边形的内角和是(10 - 2)×180。=1440。. 下面我们一起来看两个例题 例 如果一个四边形的一组对角互补,那么另一组对角有什么关系? 根据题意画图,在四边形 ABCD 中,
5 分 巩固新知 已知经A + 经C = 180。, :经A + 经B + 经C + 经D = 360。 :经B + 经D = 360。一 (经A + 经C) = 360。一 180。= 180。 A C D B
(
B
) (
E
)所以如果一个四边形的一组对角互补,那么另一组对角也互补. 例 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六 边形的外角和.六边形的外角和等于多少? 4 D 5 F 3 6 C (
A
)2 1 因为六边形的任何一个外角加上与它不相邻的内角都等于180。,因此六 边形的 6 个外角加上它们相邻的内角,所得的总和等于 6x 180。. 所以外角和为 6 x 180。一(6-2). 180。=2 x 180。=360。 同学们也可以像这样理解,为什么多边形的外角和等于 360 度? 如图,从多边形的一个顶点 A 出发,沿多边形的各边走过各顶点,再回 到点 A,然后转向出发时的方向.在行程中所转的各个角的和就是多边形 的外角和.由于走了一周,所转的各个角的和等于一个周角,所以多边形
的外角和等于 360 度. A
所以任何多边形的外角和都等于 360。,不随边数的改变而改变. 请同学们根据所学习的新知来做一组练习: 求出下列图形中x 的值.
1 分 课堂小结 根据四边形的内角和是 360,已知一个角是 90,另一个角是 140,可得 x=65 一个多边形的内角和是 1620 ° , 它是 边形. 根据多边形的内角和公式,可得 (n - 2)×180。= 1620。,解方程得 n=11 所以十一边形. 一个多边形的每一个外角都等于 30 ° , 则这个多边形为 边形. 由一个多边形的每一个外角都等于 30 °多边形的外角和是 360,用 360 除以 30 可得这个多边形是十二边形. 一个多边形的内角和与外角和相等,它是几边形? 由多边形的内角和与外角和相等,可得方程为 (n - 2)×180。=360 解得 n=4,所以多边形的内角和与外角和相等是四边形. 课堂小结,本节课我们学习了 1.把多边形的问题可以转化为三角形的问题来研究,将未知转化为已 知. 2.多边形的内角和为 (n - 2)×180。,内角和仅与边数有关,与多边形的 大小无关,边数每增加 1,内角和增加180。. 3. 多边形的外角和为 360。,不随边数的改变而改变.
2 分 布置作业 教科书 P24-25 复习巩固 2,3 , 4,5 , 6.
教学目标
教学目标:探索并证明多边形的内角和定理及外角和定理,并进行相关的计算与证明. 教学重点:探索并证明多边形内角和定理. 教学难点:把多边形问题转化为三角形问题的研究方法.
教学过程
时间 教学环节 主要师生活动
2 分 知识回顾 上节课我们学习了多边形的定义及相关概念,探究了对角线的条数与边 数 n 的关系,下面我们一起来回顾 1.多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做 多边形.如果一个多边形由 n 条线段组成,那么这个多边形叫做 n 边形; 2.多边形相邻两边组成的角叫多边形的内角; 3.多边形边与它的邻边的延长线组成的角叫多边形的外角; 4.连接多边形不相邻的两个顶点的线段叫多边形的对角线; 5. n 边形有 n 个顶点,n 个内角,2n个外角,一个顶点可以引(n-3)条 对角线,可以把多边形分成(n-2)个三角形,多边形共有条对 角线.
A1 An A2 A4 A1 An A2 A4
A3 A3
14 分 探究新知 研究多边形的问题通过添加对角线,都可以转化为三角形.你能利用三 角形内角和定理证明,任意四边形 ABCD 的内角和等于 360。吗? 已知:四边形 ABCD ,求证: 经A+经B+经C+经D=360。. 方法 1:证明:连接AC , 经BAD + 经B + 经BCD + 经D = 经1+经2+经B + 经3 + 经4 + 经D = (经1+ 经B + 经3) + (经2 + 经D + 经4) = 180。+180。 = 360。 把一个四边形分成几个三角形,还有其他分法吗? 方法 2:如图,在四边形 ABCD 内部取一点 O , 连接 AO、BO、CO、DO 把四边形分成 四个三角形 ΔABO、ΔADO、ΔCDO、ΔCBO 所以四边形 ABCD的内角和为: 180。会 4 一 (经AOB + 经AOD + 经COD + 经COB) = 180。会 4 一 360。 = 360。 方法 3:如图,在BC 边上任取一点 O ,连接 AO、BO ,所以该四边形被分成三个三角形 ΔABO、ΔADO、ΔDCO 所以四边形 ABCD的内角和为: 180。会3 一 (经AOB + 经AOD + 经COD) = 180。会3 一 180。 = 360。 方法 4:如图,在四边形外任取一点 O , 连接 AO、BO、CO、DO 将四边形变成 有一个公共顶点的三个三角形 ΔABO、ΔADO、ΔDCO ,再减去 ΔCBO 的内角和 180,即可得四边形 ABCD 的内角和为: 180。会3 一 180。= 360。
例题解析 以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为 已学的三角形内角和进行求解. 四边形可以如此解决,多边形的问题也可以通过添加对角线转化成三角 形问题来解决. 如图 1 可得多边形的内角和为 (n - 2)×180。 如图 2 多边形的内角和 n × 180。-360。=(n - 2)×180。 如图 3 多边形的内角和(n-1)×180。-180。= (n - 2)×180。 如图 4 多边形的内角和(n-1)×180。-180。= (n - 2)×180。 通过探究得到多边形内角和公式为 (n - 2)×180。 小结: 多边形的问题可以转化为三角形的问题来研究,将未知转化为已知. 多边形的内角和仅与边数有关,与多边形的大小无关; 请问八边形的内角和是(8 - 2)×180。=1080。, 十边形的内角和是(10 - 2)×180。=1440。. 下面我们一起来看两个例题 例 如果一个四边形的一组对角互补,那么另一组对角有什么关系? 根据题意画图,在四边形 ABCD 中,
5 分 巩固新知 已知经A + 经C = 180。, :经A + 经B + 经C + 经D = 360。 :经B + 经D = 360。一 (经A + 经C) = 360。一 180。= 180。 A C D B
(
B
) (
E
)所以如果一个四边形的一组对角互补,那么另一组对角也互补. 例 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六 边形的外角和.六边形的外角和等于多少? 4 D 5 F 3 6 C (
A
)2 1 因为六边形的任何一个外角加上与它不相邻的内角都等于180。,因此六 边形的 6 个外角加上它们相邻的内角,所得的总和等于 6x 180。. 所以外角和为 6 x 180。一(6-2). 180。=2 x 180。=360。 同学们也可以像这样理解,为什么多边形的外角和等于 360 度? 如图,从多边形的一个顶点 A 出发,沿多边形的各边走过各顶点,再回 到点 A,然后转向出发时的方向.在行程中所转的各个角的和就是多边形 的外角和.由于走了一周,所转的各个角的和等于一个周角,所以多边形
的外角和等于 360 度. A
所以任何多边形的外角和都等于 360。,不随边数的改变而改变. 请同学们根据所学习的新知来做一组练习: 求出下列图形中x 的值.
1 分 课堂小结 根据四边形的内角和是 360,已知一个角是 90,另一个角是 140,可得 x=65 一个多边形的内角和是 1620 ° , 它是 边形. 根据多边形的内角和公式,可得 (n - 2)×180。= 1620。,解方程得 n=11 所以十一边形. 一个多边形的每一个外角都等于 30 ° , 则这个多边形为 边形. 由一个多边形的每一个外角都等于 30 °多边形的外角和是 360,用 360 除以 30 可得这个多边形是十二边形. 一个多边形的内角和与外角和相等,它是几边形? 由多边形的内角和与外角和相等,可得方程为 (n - 2)×180。=360 解得 n=4,所以多边形的内角和与外角和相等是四边形. 课堂小结,本节课我们学习了 1.把多边形的问题可以转化为三角形的问题来研究,将未知转化为已 知. 2.多边形的内角和为 (n - 2)×180。,内角和仅与边数有关,与多边形的 大小无关,边数每增加 1,内角和增加180。. 3. 多边形的外角和为 360。,不随边数的改变而改变.
2 分 布置作业 教科书 P24-25 复习巩固 2,3 , 4,5 , 6.
